Структурные преобразования в импульсных системах.

При анализе сколько-нибудь сложных импульсных САУ невоз­можно обойтись без структурных преобразований, сопровождающихся определением эквивалентных передаточных функций отдельных элементов цепи. Правила структурных преобразований дискретных систем имеют отличия от правил преобразования непрерывных си­стем, вызванные наличием импульсных элементов. Рассмотрим не­которые возможные структуры импульсных систем.

1.Система с импульсным элементом на входе. Структурная схема системы с ИЭ на входе, соответствующая этому случаю, была рассмотрена ранее (см. рис. 8) и получены соотношения

2.Последовательное соединение непрерывных звеньев, раз­деленных импульсными элементами. Структурная схема системы в этом случае представлена на рис.12. Разбив схему на части, каждая из которых состоит из одного непрерывного звена и им­пульсного элемента перед ним, получим

Рис.12

Исключив промежуточные переменные, найдем

т.е. Z -передаточная функция последовательного соединения звеньев, разделенных ИЭ, равна произведению z-передаточных функций этих звеньев.

3. Последовательное соединение непрерывных звеньев с одним импульсным элементом на входе. Структурная схема данной системы представлена на рис.13.

Рис.13

В этом случае эквивалентная передаточная функция непре­рывной части имеет вид

после чего соединение сводится к схеме 1. т.е.

4. Параллельное соединение непрерывных звеньев с импульс­ным элементом на входе. Структурная схема системы показана на рис.14. В соответствии с определением Z-передаточной функции и свойством линейности -преобразования имеем

где

т.е. Z-передаточная функция соединения равна сумме Z -пере­даточных функций отдельных звеньев, составлявших параллельное соединение.

5. Элементарная структура соединения с обратной связью. Структурная схема этой системы представлена на рис.15.

Рис. 14. Рис. 15.

На основании результата п. 1 запишем

где

Добавив уравнение замыкания

и исключив из зависимостей получим выражение для передаточной функции соединения

.

В частном случае при имеем и приходим к результату, полученному ранее.

В общем случае вычисление эквивалентной передаточной функции системы с большим числом импульсных элементов можно производить в следующей последовательности:

1. Ввести вспомогательные переменные, приняв за них сиг­налы на входах ИИЭ, входящих в схему.

2. Связать введенные вспомогательные координаты, входную и выходную переменные системы между собой с помощью Z-пере­даточных функций.

З. Исключить промежуточные переменные и разрешить запи­санную систему уравнений относительно выходной переменной.

4. Записать эквивалентную Z -передаточную функцию си­стемы.

Пример. Найти Z-передаточную функцию импульсной системы, структурная схема которой представлена на рис.16.

 

Рис.16

Введем вспомогательные переменные и запишем си­стему уравнений в изображениях:

где

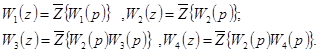
Выполнив промежуточные преобразования, получим

откуда следует

и тогда

Таким образом, эквивалентная z-передаточная функция системы по входному сигналу имеет вид

 

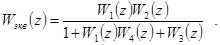
Лекция 6

 

Частотные характеристики дискретных систем.

 

План лекции:

1. Определение установившейся реакции импульсной системы на дискретный гармонический сигнал.

2. Частотные характеристики дискретных систем.

3. Свойства частотных характеристик импульсных систем.

 

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: