 |
Реализация цифровых регуляторов на микроЭВМ.
|
|
|
|
Это наиболее универсальный способ. Передаточная функция регулятора может быть реализована в виде программы для ЭВМ. Известны три основных метода программирования: прямое, параллельное и последовательное. С аналитической точки зрения они непосредственно связаны с методами выборо переменных состояния. По существу, при использовании какого-либо из этих способов мы соответствующим способом получаем совокупность уравнений состояния и уравнение для выходной переменной и далее составляем алгоритм решения данных уравнений на ЭВМ. Таким образом, каждый из этих способов программирования отличается системой уравнений, решаемой на ЭВМ.
Рассмотрим передаточную функцию цифрового регулятора. Расчет на ЭВМ ведется в реальном времени. При m<n значение x[kT] определяется прошлыми значениями х и прошлыми значениями е. При этом быстродействие ЭВМ долно быть таким, чтобы за время Т выполнить все необходимые расчеты. При m=n быстродействие ЭВМ должно обеспечивать расчет за время, пренебрежимо малое с величиной Т или необходимо учитывать величину запаздывания, вносимую ЭВМ.
Пример:
имеем систему
 |
рис.52
пусть
Необходимо синтезировать цифровой регулятор с учетом следующих требований:
— устоновившаяся ошибка при отработке сигнала f(t)=t Eуст<=0.33
— запас по фазе >= 50
— показатель колебательности М<=1.3
Z-передаточная функция разомкнутой САУ без коррекции имеет вид:
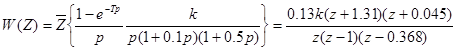
В нескорректированой системе в установившемся режиме имеем:
f(t)=t;
y(t)=t-A А*К=1 и следовательно А=1/К
Eуст=А А<0.33 и тогда К>=3
На рис. 52 представлены ХПЧХ данной передаточной функции.
Из характеристик видно, что при К=3 система без коррекции находится практически на границе устойчивости. Запасы почти нулевые. Можно показать, что Ккр=3.3; для обеспечения запаса устойчивости по фазе 50 при сохранении коэффициента К=3 предлагается использовать регулятор с отставанием по фазе. Регулятор с опережением фазы (ИДФ с преобладанием дифференцирования в данном случае будет неэффективен из-за резкого завала фазы в районе -180)
|
|
|
Выберем D*(w) в виде
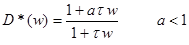
Для получения запаса =50 частоту среза нужно сдвинуть из (.) l=2.4 в точку l=0.8 при условии, что регуляторD*(w) не окажет на новой частоте среза существенного влияния на ФЧХ. ЛАФЧХ показывает, что Н*(0.8)=12дб. Следовательно D*(w) на частоте 0.8 должен вносить ослабление -12дб. Из этих соображений находим “а”
20lg a=-12 дб; a=0.25;
Чтобы фазовая характеристика D*(w) не влияла на фазовый сдвиг САУ при l=0.8 выберем частоту, соответствующую правому излому D*(w) на декаду меньше значения 0.8, таким образом
1/at=0.08 и 1/t=0.02
W-передаточная функция цифрового регулятора принемает вид:
ЛАФЧХ скорректированой системы представлены на рисунке 52. Теперь
 |
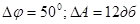
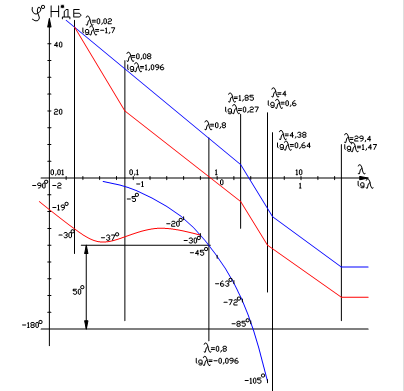Рис. 52.
Если перенести ЛАФПЧХ на номограмму замыкания, то можно видеть, что ранее М было практически бесконечным, в скорректированой САУ М=1.2
Передаточная функция D(z) получается подстановкой в D*(w)
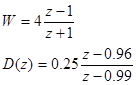
Чтобы убедиться в правильности решения задачи синтеза запишем передаточную функцию замкнутой системы
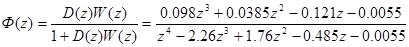
Переходная характеристика представлена на рисунке:
 |
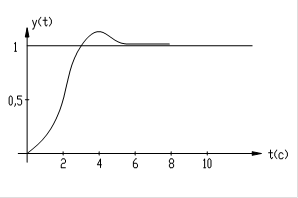рис.53
Заключительный этап синтеза включает в себя реализацию D(z) каким-либо из рассмотренных способов.
Лекция 23
Синтез ЦСУ с апериодическим переходным процессом.
План лекции:
1. Общие положения.
2. Пример решения задач синтеза ЦСУ с минимальным временем ПП.
3. Общий случай синтеза системы с апериодическим переходным процессом.
Общие положения.
Рассмотренные способы синтеза базировались на основе непрерывных систем, использующих ЛАФЧХ, регуляторы с опережением или отставанием по фазе. Однако структура ЦР отличается большой гибкостью, поэтому можно разработать оригинальные методы, отличные от метода синтеза непрерывных САУ.
|
|
|
Большая часть СУ проектируется так, чтобы переходный процесс в них возможно быстрее достигал требуемого значения. Этот класс систем называется системами с минимальным временем переходных процессов или системами оптимальными по быстродействию. Решение задач синтеза ЦСУ с минимальным временем ПП рассматривается далее.
Пример.
Рассмотрим пример:
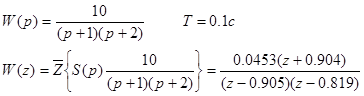
Пусть последовательный цифровой регулятор имеет ПФ
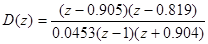
Тогда ПФ разомкнутой скорректированой системы
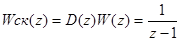
То есть введение КУ приводит к компенсации всех нулей и полюсов исходной системы и появлению нового полюса Z=1
Соответствующая ПФ замкнутой системы:
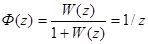
Тогда при ступенчатом входном сигнале
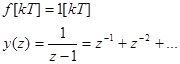
Это означает, что выходной сигнал у[kT] достигает требуемого значения за один период квантования и с этого момента сохраняет требуемое значение. Перерегулирование нулевое. Однако в общем случае, хотя у(кТ) может иметь малое перерегулирование, действительная реакция у(t) может сопровождаться импульсами.
Так как Т<< постоянных времени объекта, можно ожидать, что y[kT] достаточно хорошо совпадает с y(t). Поэтому можно ожидать, что переходная функция достигает установившегося значения через Т=0.1с, а между моментами квантования пульсаций не будет или они будут малы. Такой тип реакции называется апереиодическим переходным процессом.
Апериодический переходный процесс можно получить только в случае, когда есть полная компенсация нулей и полюсов. На практике реальное ограничение приводит к тому, что достичь идеального апериодического процесса невозможно.
 |
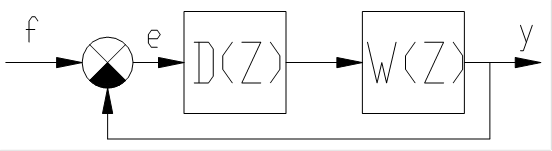
3. Общий случай синтеза системы с апериодическим переходным процессом.
Рис. 54.
Что должно быть в результате синтеза:
1. Нулевая установившаяся ошибка при определении входного сигнала.
2. Длительность переходного процесса должна быть минимальной
3. Цифровой регулятор должен быть физически реализуемым
ПФ замкнутой скорректированной системы имеет вид:
|
|
|
(1)
откуда
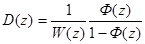(2)
при этом
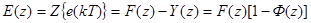(3)
Будем рассматривать класс входных сигналов, изображение которых имеет вид:
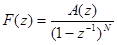(4)
где N-натуральное число
A(z)- многочлен от z
В общем случае выражение (*) соответствует входному сигналу типа
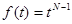
Например, при
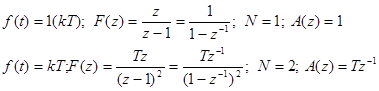
С учетом (*), используя теорему определьном значении найдем установившуюся ошибку
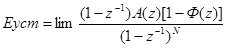(5)
Исходя из полученного выражения выясним, что необходимо, чтобы Еуст=0. Так как А(1)<>0,то очевидно, что для этого 1-Ф(z) должно содержать скобку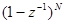 
т.е.
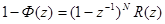(6)
где R(z)-полином от Z
Следствием того, что 1-Ф(z) представимо в форме (6) будет выражение:
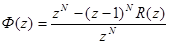
Полюсы Ф(z) могут возникать как:
— нули знаменателя Z=0
— полюсы числителя, так как R(z)-многочлен от Z, то это может быть только Z=0
Таким образом, при сделанных предложениях, Ф(z) имеет единственный полюс Z=0. Характеристическое уравнение имеет вид:
Подставив (6) и (4) в (3) получим
E(z)=A(z)R(z) — это Z-преобразование ошибки.
При этом, так как A(z) и R(z) -полиномы от Z, то E(z) тоже полином от Z и следовательно E(z) имеет конечное число членов при разложении в ряд по степеням Z. Таким образом, пр исделанных предложениях сигнал ошибки сводится к нулю за конечное число периодов квантования.
Таким образом, синтез цифрового регулятора может проводиться так
R(z)®Ф(z)®D(z)
При этом необходимо иметь физически реализуемую ПФ. Это можно проконтролировать при выборе Ф(z)
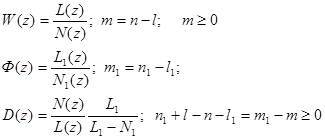
разность степеней числителя и знаменателя не меньше, чем у W(z), это необходимо учитывать при определении Ф(z). Вернемся к соотношению(6). N определяется типом входного сигнала. Тогда
N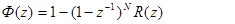 
ступенчатый сигнал 1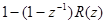 
линейный 2 
парабола 3 
Видно, что при этом для ступенчатого сигнала минимальное время установления е=0 составляет один такт, для линейного — 2 такта и т.д.
Рассмотренный алгоритм определения D(z) имеет ряд особенностей:
1. Если W(z) имеет нули на единичной окружности или вне ее, то будет нужен енустойчивый регулятор. Этот случай нужно рассматривать отдельно
2. В таблице m=1 и должно быть, чтобы m<=1
Таким образом: если есть такие нули или m>1, то R(z) не может быть 1
|
|
|
Пример:
Пусть
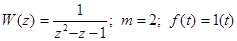
Нельзя взять Ф(z)=1/z из таблицы
Попробуем взять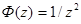 
, тогда
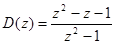
При этом
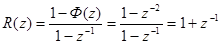
и процесс заканчивается за два такта.
В общем случае при заданном входе, определяющем N, минимальное число переиодов квантования, составляющих переходный процесс, равно
N+m-1
Лекция 24
|
|
|
