 |
Определение установившейся реакции импульсной системы на дискретный гармонический сигнал.
|
|
|
|
Рассмотрим прохождение дискретного гармонического сигнала
.
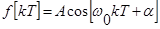через импульсную систему с передаточной функцией 
. Для этого найдем реакцию системы на воздействие
(31)
и далее выделим ее действительную часть,
Найдем изображение сигнала (31). На основании формулы (20) получим
.
Изображение выходной переменной системы имеет вид
.
Вычислив обратное Z-преобразование, найдем реакцию импульсной системы на сигнал (31):
где 
- особые точки выражения, стоящего под знаком вычета, т.е. это полюсы передаточной функции и точка 
.
Положим для простоты, что полюсы 
передаточной функции некратные и удовлетворяют условию
(32)
Тогда
или
(33)
где
.
При выполнении условия (32) второе слагаемое правой части формулы (33) стремится к нулю при 
и в системе устанавливается вынужденное движение
(34)
Выделив в выражении (34) действительную часть, получим реакцию системы на гармонический сигнал в виде
.
Из последней формулы видно, что при прохождении дискретного гармонического сигнала через импульсную систему у него изменяются амплитуда и фаза: амплитуда увеличивается в 
раз, а фаза изменяется на 
.
Частотные характеристики дискретных систем.
Выражение 
, полученное из Z-передаточной функции подстановкой 
, называется амплитудно-фазовой частотной характеристикой (АФЧХ) импульсной системы. Функция 
называется амплитудной частотной характеристикой, функция 
- фазовой частотной характеристикой импульсной системы. АФЧХ импульсной системы позволяют найти установившуюся реакцию на гармоническое воздействие, и в этом они сходны с АФЧХ непрерывных систем. АФЧХ импульсных систем определяют по следующим формулам:
, (38)
, (39)
|
|
|
. (40)
Пример. Пусть 
. Найти частотные характеристики звена с такой передаточной функцией.
В соответствии с определением имеем
;
;
.
 |
Графики АФЧХ, построенные по приведенным зависимостям, показаны на рис.17 (здесь
).
Рис.17
Из рис.17 видно, что частотные характеристики импульсных систем существенно отличаются от АФЧХ непрерывных систем, изучаемых в курсе "Основы ТАУ".
Свойства частотных характеристик импульсных систем.
Рассмотрим некоторые свойства частотных характеристик импульсных систем.
1.Вследствие периодичности экспоненты 
частотная характеристика дискретной системы является периодической функцией частоты с периодом 
. Поэтому АФЧХ импульсной системы полностью определяется значениями в диапазоне 
(в основной полосе). Периодичность АФЧХ приводит к тому, что импульсная система одинаково пропускает сигналы 
и 
, так как в обоих случаях на выходе ИИЭ существуют одинаковые последовательности импульсов. Это свойство импульсных систем поясняет рис.18.
 |
Рис. 18
2. Амплитудно-частотная характеристика 
является четной функцией частоты, т.е. 
Вследствие четности АЧХ и периодичности достаточно знать значения АЧХ в диапазоне 
.
Фазово-частотная характеристика 
является нечетной функцией частоты, т.е. 
.
Она также может быть задана своими значениями в диапазоне .
3. При частотах 
, где 
частотная характеристика дискретной системы всегда принимает действительные значения:
или
.
Это свойство выполняется за исключением случаев, когда передаточная функция ПНЧ 
имеет полюс 
порядка m.Тогда передаточная функция W(z) имеет полюс z=1 того же порядка m и при 
.
Лекция 7
Вычисление частотных характеристик дискретных систем.
План лекции:
1. Псевдочастотные характеристики импульсных систем.
2. Методы построения частотных и псевдочастотных характеристик дискретных систем.
|
|
|
|
|
|
