 |
Пример составления математического описания импульсной системы.
|
|
|
|
Рассмотрим более подробно математическое описание подобных систем на примере. Пусть структурная схема дискретной системы имеет вид, представленный на рис.39,а. Данная система является асинхронной. Периоды повторения первого ИЭ Т и второго кратные числа, причем T=2T1. Формирующие звенья обоих импульсных элементов представляют собой экстраполяторы нулевого порядка. Временная диаграмма работы импульсных элементов представлена на рис.39.б.
Примем за переменные состояния координаты x1,x2. Входное воздействие u(t) будем считать непрерывной функцией. Рассмотрим временной интервал (kT,t1) и запишем дифференциальные уравнения, соответствующие переходу


 |
Рис. 39
Решив данную систему, получим при 


Подставим  найдем
найдем

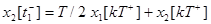
Представим систему в виде

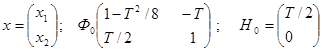
Рассмотрим далее дискретный переход 
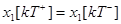

т.е.
 (83)
(83)
где
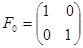 .
.
Объединив результаты двух рассмотренных переходов, получим

или
 (84)
(84)
так как для данного случая  .
.
Рассмотрим следующий временной интервал  Запишем дифференциальные уравнения, соответствующие переходу
Запишем дифференциальные уравнения, соответствующие переходу  . При этом следует иметь в виду, что в момент времени t1 срабатывает только второй ИЭ, а выходной сигнал первого ИЭ не меняется. Уравнения имеют вид
. При этом следует иметь в виду, что в момент времени t1 срабатывает только второй ИЭ, а выходной сигнал первого ИЭ не меняется. Уравнения имеют вид

Решив данную систему, получим при 


При t=(k+1)T имеем  и тогда
и тогда


или, переходя к матричной форме записи,
 (85)
(85)
где

Дискретный переход 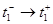 аналогичен рассмотренному дискретному переходу
аналогичен рассмотренному дискретному переходу  , т.е.
, т.е.
 (86)
(86)
Объединив выражения (83), (85). (86), получим
 (87)
(87)
Подставляя в зависимость (87) выражение для  , будем иметь
, будем иметь

или
 (88)
(88)
где
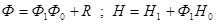
Таким образом, получена система разностных уравнений (88), определяющая связь между значениями переменных состояния на интервале основного квантования Т. Устойчивость рассматриваемой дискретной системы определяется собственными числами матрицы Ф. Полученные зависимости позволяют провести расчет переходных процессов в данной системе.
|
|
|
Лекция 18
Особенности вынужденных процессов в импульсных системах.
План лекции:
1. Свободный и вынужденный процессы в импульсных системах.
2. Расчет вынужденных процессов с помощью моментов весовой характеристики
3. Процессы конечной длительности в импульсных системах.
Свободный и вынужденный процессы в импульсных системах
Точность воспроизведения входных воздействий является одной из наиболее важных характеристик импульсных систем. При исследовании точности рассматриваются вынужденные процессы, т.е. процессы, устанавливающиеся по истечении бесконечно большого промежутка времени после подачи входного воздействия. Остановимся на аналитическом способе определения вынужденного процесса в импульсной системе.
Реакция импульсной системы (безразлично, замкнутой или разомкнутой) на входное воздействие  определяется по выражению
определяется по выражению
 (89)
(89)
где  -импульсная переходная функция системы, связанная с ее Z-передаточной функцией зависимостью
-импульсная переходная функция системы, связанная с ее Z-передаточной функцией зависимостью

Формула (89) описывает процесс в системе при условии, что входное воздействие приложено в моменты k=0. При произвольном моменте приложения воздействия  она принимает вид
она принимает вид
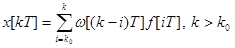 .
.
Полагая  , получим, что между приложением входного воздействия и настоящим моментом прошел бесконечно большой промежуток времени. Назовем процесс, соответствующий этому условию, вынужденным процессом импульсной системы. Обозначая его
, получим, что между приложением входного воздействия и настоящим моментом прошел бесконечно большой промежуток времени. Назовем процесс, соответствующий этому условию, вынужденным процессом импульсной системы. Обозначая его 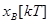 , будем иметь
, будем иметь

или, заменяя переменную i на переменную j по формуле k-i=j,
 (90)
(90)
Свободным процессом импульсной системы назовем разность между общим процессом (89) и вынужденным процессом (90), т.е.
 (91)
(91)
|
|
|


