 |
Уравнения состояния дискретных систем
|
|
|
|
Способ математического описания дискретных систем разностными уравнениями является наиболее общим и применяется как для линейных, так и для нелинейных систем. Разностные уравнения позволяют провести полное исследование системы, они хорошо приспособлены для решения задач анализа и синтеза с помощью ЭВМ
 |
Вопрос о составлении разностных уравнений импульсной системы
Рис. 33
удобно рассмотреть сразу для многомерной САУ. Уравнения для системы с одним входом и одним выходом получатся тогда как частный случай.
Рассмотрим многомерную синхронную синфазную импульсную систему (рис.33). Импульсные элементы в этой схеме имеют одинаковые частоты квантования и работают синфазно. Пусть непрерывная часть системы описывается уравнением
(53)
(54)
где 
-мерный вектор переменных состояния; 
-мерный вектор входных воздействий, 
-мерный вектор выходных переменных.
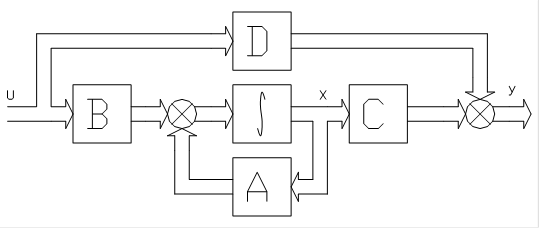
Матрицы A,B,C,D имеют следующие размерности: A-(n´n) матрица, B-(n´m) матрица, C-(r´n) матрица и D-(r´m) матрица. Графически уравнениям (53), (54) соответствует структурная схема, представленная на рис.34. Здесь и далее двойные стрелки на схеме указывают на то, что связи относятся к векторным величинам.
Матрица A - основная или собственная матрица системы. Она определяет устойчивость системы, характер ее свободных движений Матрица B - матрица формирования управления. Она определяет передаточные свойства системы и характеристики вынужденного движения. Матрица C определяет связь между выходными переменными и переменными состояния, матрица D устанавливает непосредственную зависимость выходных координат системы от входных переменных,
Рис. 34
 |
Рассмотрим решение дифференциального уравнения (53) при заданных начальных условиях
и известных входных воздействиях u(t). Как известно, общее решение неоднородного дифференциального матричного уравнения с постоянными коэффициентами имеет вид|
|
|
,
где X(t) - произвольная фундаментальная матрица соответствующего однородного дифференциального уравнения. Выбрав в качестве X(t) нормированную фундаментальную матрицу (для стационарной системы она имеет вид 
), получим
. (55)
Предположим, что в качестве формирующего звена используется экстраполятор нулевого порядка. Тогда в течение каждого из интервалов квантования 
на вход непрерывной части поступает постоянный сигнал u(t)=const=u[kT]. Полагая известными значения переменных состояния при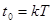 
, найдем их значения при t=(k+1)T. Подставив соответствующие значения в уравнение (55), получим
. (56)
Таким образом, получена система разностных уравнений в матричной форме, определяющая значения переменных состояния на k+1 такте через значения вектора состояния и вектора входных воздействий на предыдущем шаге. Векторное уравнение (56) можно представить в виде
Дополняя его дискретным аналогом уравнения (54), получим окончательную систему разностных уравнений в виде
(57)
(58)
где Ф - собственная матрица импульсной системы, 
; H матрица входа,
; Е- единичная матрица соответствующей размерности. Матрицы С и D при переходе от уравнений (54) и (58) не изменяются.
Таким образом, получена система разностных уравнений, описывающая рассматриваемую импульсную систему.
3. Некоторые способы вычисления переходной матрицы.
Из выражений для матриц Ф и Н, входящих в уравнение (57) легко видеть, что основные сложности при переходе от системы (53), (54) к системе разностных уравнений (57), (58) заключаются в вычислении собственной матрицы , которая является переходной матрицей непрерывной части. Для ее нахождения используют как аналитические, так и численные методы.Наиболее часто аналитические методы связаны с решением однородного дифференциального уравнения
|
|
|
(59)
при произвольных начальных условиях 
. Применяя для решения уравнения преобразование Лапласа, получаем
,
где 
. Отсюда
и тогда
.
Из последнего соотношения следует, что
Существуют и другие аналитические методы нахождения матрицы [2]. Однако все аналитические методы отличаются сложностью и трудоемкостью, которые возрастают с ростом размерности вектора состояния системы.
Численные методы определения матрицы основаны на вычислении суммы матричного ряда
где 
- число удерживаемых членов бесконечного ряда.
Недостаток вычисления матрицы Ф по этому методу - плохая сходимость степенного разложения, которая вместе с учетом конечной разрядности ЭВМ может привести к существенным погрешностям в вычислениях (вплоть до неверного определения знака у элементов матрицы Ф).
Лучшей сходимостью обладают алгоритмы, основанные на использовании степенных рядов, полученных в результате разложения по полиномам Чебышева [2]. Наконец, элементы матрицы Ф могут быть получены в результате повторного n -кратного численного решения дифференциального уравнения (59). После численного интегрирования в интервале от 0 до Т уравнения (59) для 
, найденный вектор x(T) при t=T будет представлять собой первый столбец матрицы Ф. Аналогично, решив численно уравнение (59) при 
, получим второй столбец матрицы Ф, а в результате n-кратного интегрирования матрица Ф будет определена полностью. Таким же способом можно численно вычислить и матрицу Н. Для этого необходимо проинтегрировать m раз уравнение (53), положив x=0 и приравнивая к единице поочередно компоненты вектора входных воздействий u.
Лекция 13
|
|
|
