 |
ОСНОВНАЯ ЧАСТЬ. Конфликт третьего закона термодинамики с законом сохранения энергии
|
|
|
|
ОСНОВНАЯ ЧАСТЬ
Учитывая, что вакуум может взаимодействовать с физическими телами или окружающим нас реальным миром, можно сказать, что современные достижения в области физики вакуума и элементарных частиц, практически полностью меняют основы традиционного научного мышления – традиционные, фундаментальные законы сохранения массы и энергии. Как видим, по современным представлениям, масса и энергия могут порождаться из ничего (из вакуума) и наоборот они могут исчезнуть, скрыться в глубину невозмущенной материи.
В таких условиях, такие фундаментальные отрасли науки, как феноменологическая термодинамика и механика сплошной среды приобретают смысл системы ограниченных или упрощенных законов, которые с хорошей точностью отражают очень широкий спектр физических явлении, но никак не могут охватить все множество процессов, которые характерны для окружающего нас мира.
Следовательно, возникает вопрос, можно или нет усовершенствовать феноменологическую термодинамику с учетом современных достижении в области теории вакуума? Как можно изменить законы термодинамики с учетом такой реальности?
В данной работе делается попытка внесения некоторых изменении в уравнениях термодинамики, хотя, учитывая что, в виде энергии вакуума, мы имеем бесконечную, еще не до конца изученную субстанцию, конечно, приведенные суждения не имеют претензию на полное совершенство и правомерность предложенных результатов наверно будет доказана или отторгнута со временем.
При рассмотрении данного вопроса мы учитываем что:
1. С точки зрения строения атомов и молекул, подавляющая часть объема любого физического тела занята вакуумом (расстояние между ядром атома и его электронной оболочкой на несколько порядка больше чес размер самого ядра).
|
|
|
2. Вакуум, который находится внутри любого физического тела, по всей видимости, может рассматриваться как внутренний источник или резервуар энергии а энергия вакуума, или ее определенная часть, при определенных условиях, может принимать участие в термодинамических процессах, которые происходят внутри тела.
Для обоснования актуальности поставленного вопроса, следует отметить, что такой подход позволяет объяснить конфликты между классическими законами термодинамики. В частности, ниже мы покажем, что, если в окрестности абсолютного нуля, изохорная теплоемкость является функцией только температуры, как это показано в теориях Дебая и Эйштейна, то между первым законом (закон сохранения энергии) и третьим законом (закон Нернста) возникает явный конфликт, который исчезает, если учтем участие энергии вакуума (или энергии поля) в термодинамических процессах.
Конфликт третьего закона термодинамики с законом сохранения энергии
В первую очередь рассмотрим, как зависит классическая изохорная теплоемкость от термодинамических параметров состояния. Для этого, применяют закон сохранения энергии
, (1)
При этом, в общем случае, нормальное давление 
можно выразить как сумму функции холодного давления 
и термодинамического давления 
, которое исчезает при нулевой температуре
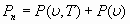. (2)
Путем деления уравнения (1) на температуру получается уравнение для приращения энтропии или выражение для полного дифференциала энтропии. Используя свойства полного дифференциала, нетрудно показать, что [1]:
, (3)
или
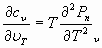. (4)
Интересно, что, для большого множества тел, в довольно широком интервале изменения параметров состояния, изохорная теплоемкость зависит только от температуры.
, (5)
Поэтому, для таких тел
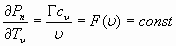. (6)
Последнее выражение показывает, что, при нагреве тела в замкнутом объеме, нормальное давление должно возрастать пропорционально температуры а произведение параметра Грюнайзена (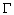 
) на изохорную теплоемкость должно являться постоянной величиной. К примеру, для реального газа Ван-Дер-Ваальса имеем:
|
|
|
. (7)
Следовательно, для реального одноатомного газа Ван-Дер-Ваальса изохорная теплоемкость зависит только от температуры.
Интересно, что теплоемкость твердого тела, как правило, также зависит только от температуры. Для описания термодинамических свойств кристаллов твердого тела, в 1912 году, П. Дебаем была предложена теория, описывающая колебания кристаллической решётки. Данная теория основана на условном представлении твёрдого тела как изотропной упругой среды, атомы которой совершают колебания в конечном диапазоне частот. Кристаллическая решётка, состоящая изN элементарных ячеек по v атомов в каждой, имеет 
колебательных степеней свободы. С механической точки зрения, такую систему можно описывать как совокупность независимых механических осцилляторов, каждый из которых соответствует отдельному нормальному колебанию системы. Вычисление термодинамических функции такой системы в общем виде невозможно, т. к. результат существенно зависит от конкретного распределения частот по спектру колебаний твёрдого тела. Однако в предельных случаях статистическая сумма и термодинамические функции кристаллической решётки могут быть вычислены.
В случае высоких температур возбуждены все колебательные степени свободы и на каждую приходится энергия kT (закон равнораспределения). В таком случае для теоретической теплоемкости твердых тел получается закон Дюлонга и Пти
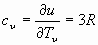. (8)
В предельном случае низких температур возбуждаются только колебания низких частот, которые представляют собой звуковые волны с линейным законом дисперсии. Соответственно, получается Дебая закон теплоёмкости:
, (9)
В частности, при малых Т верхний предел интегрирования стремится к бесконечности и получается формула:
. (10)
Здесь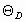 
- выражает температуру Дебая, выше которой возбуждены все моды кристалла, а ниже которой некоторые моды начинают " вымерзать".
|
|
|
. (11)
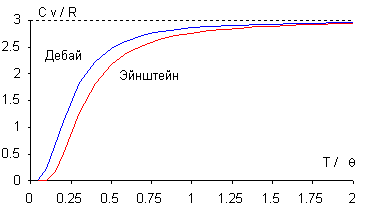
Теория Дебая хорошо передаёт температурную зависимость термодинамических функций, в частности теплоёмкости, для тел с простыми кристаллическими решётками, т. е. для большинства элементов и ряда простых соединений. К телам с более сложной структурой она менее применима из-за сложности спектра колебаний решётки. При рассмотрении решётки с многоатомным базисом (больше 1 атома в узле) существенны оптические колебания, частота которых меняется незначительно и, поэтому, здесь лучше применима теория теплоёмкости Эйнштейна, в которой всем колебаниям приписывается одна и та же частота. Формула Эйнштейна так же указывает на зависимость изохорной теплоемкости от температуры и она не отражает влияние других термодинамических параметров.
В общем случае, из-за участия в тепловых свойствах разнообразных движений, присущих твердым телам, температурная зависимость большинства характеристик очень сложна. Однако, основным фактором изменения теплоемкости считается температура.
|
|
|
