 |
Рис.3. диаграмма для определения внутренней энергии тела.
|
|
|
|
Рассмотрим на 
диаграмме произвольную точку 
. В данное состояние тело может оказаться разными путями. К примеру, тело можно сжимать адиабатически или изотермически (процесс 0-1 на рис. 3) а затем нагревать в условиях постоянного объема (линия 1-A). В процессе теплоизолированного изменения объема работа совершается нормальными поверхностными силами 
. В общем случае нормальное давление можно представить в виде суммы термодинамического давления 
и сил межмолекулярного, электростатического происхождения 
, которые являются функциями только межмолекулярных расстоянии 
(или удельного объема). Для определения нормальных сил можно использовать модель Эйнштейна по Мелвину-Хьюзу:
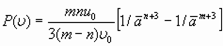, (24)
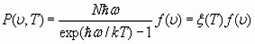, (25)
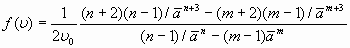, (26)
. (27)
Как видим из (25), при нулевой температуре 
. Соответственно, нормальное давление определяется из уравнения (24) и работа нормальных поверхностных сил (или приращение полной энергии в точке 1), при заданном значении удельного объема определяются однозначно как функции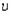 
.
, (28)
. (29).
или
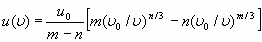. (30)
В процессе изохорного нагрева 1-A система получает тепло, которое определяется на основе реального (эмпирического) значения изохорной теплоемкости - 
, которая, в принципе, может отличаться от 
поэтому, в точке A суммарная энергия принимает вид.
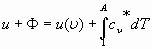, (31)
Дифференцирование (31) дает
, (32)
или
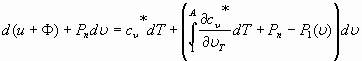(33)
Далее используем тождество, связывающее энтропию с параметрами состояния
. (34)
В таком случае получаем:
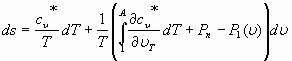. (35)
Учитывая, что энтропия является полным дифференциалом, из (35) следует:
. (36)
и для полного приращения энтропии получаем:
, (37)
С другой стороны, уравнение (34) можно представить в следующем виде:
, (38)
Поэтому, сравнивая (37) и (38) получаем
|
|
|
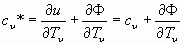, (39)
. (40)
Как уже отмечалось, при нулевой температуре приращение энтропии равно нулю, поэтому из (38) и (28) имеем
. (41)
И (40) можно представить как
, (42)
Путем дифференцирования (42) по времени, получается выражение для скорости материализации энергии вакуума
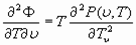, (43)
Или
, (44)
А путем простого преобразования (44) получается зависимость энергии вакуума от объема (от сжатия-расширения)
, (45)
где
. (46)
Интегрирование (45) по объему позволяет определить энергию вакуума
, (47)
А для реальной изохорной теплоемкости будем иметь:
. 
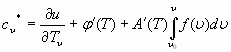, (48)
Для получения общего выражения энергии вакуума требуется знание уравнения состояния в общем виде, что практически невозможно. Вместе с тем, на основе (44), можно определить приращение энергии вакуума в каком-то конкретном процессе. В частном случае, если представляет интерес активизация вакуума в процессе нагрева пара, можно применить уравнение состояния Редлиха – Квонга [3]
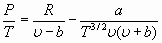, (49)
Соответственно, если пар, с начальными параметрами насыщения 
и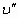 
изменяет свое состояние, то данный процесс должен привести к изменению виртуальной энергии вакуума на величину
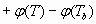, (50)
или, после дифференцирования
, (51)
и, изменение изохорной теплоемкости газа или пара, с учетом (39), можно искать из уравнения
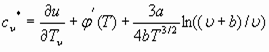, (52)
Первый член в правой части данного уравнения выражает теплоемкость жидкости до начала кипения. Как видим, разность между теплоемкостями воды и пара при одинаковой температуре обусловлена активизацией энергии вакуума в процессе кипения. Зная теплоемкость воды и пара, при определенной температуре, из (52) можно определить 
и, затем, функцию 
. Можно показать, что последняя функция зависит от скачкообразных изменении теплоемкости в фазовых переходах.
Основываясь на предложенную модель, из уравнения энергии, или на основе (38), получаем выражения для процессов плавления и парообразования
|
|
|
(53)
(54)
где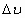 
- изменение удельного объема при плавлении. Холодная энергия 
определяется из (30), 
, 
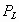- температура и давление плавления, 
, 
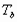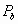- температура и давление кипения.
Из последних уравнении следует, что теплота фазовых превращении расходуется не только на увеличение потенциала межмолекулярных взаимодействии и совершение работы расширения, но и на изменение энергии вакуума.
|
|
|
