 |
Рис. 1. Изменение изохорной теплоемкости в зависимости от температуры.
|
|
|
|
Рис. 1. Изменение изохорной теплоемкости в зависимости от температуры.
Таким образом, если в интервале температур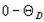 
, теплоемкость твердых тел теоретически зависит только от температуры, то после его нагрева в условиях постоянного удельного объема 
(объем, или функция расстояния между молекулами, при котором давление имеет нулевое значение) его внутренняя энергия будет являться функцией температуры.
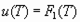. (12)
Если, после изохорного нагрева, будем менять объем тела (или расстояние между молекулами) от 
до 
, то его внутренняя энергия изменится в соответствии с потенциалом Ленарда-Джонса, Бакингема, или какого либо другого характера. Вместе с тем, как правило, принято, что такое изменение энергии зависит только от изменения межмолекулярного расстояния (или удельного объема). Соответственно, внутренняя энергия в таком процессе изменится на величину
, (13)
и, внутренняя энергия твердого тела будет иметь значение
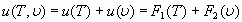, (14)
Таким образом, в крайнем случае, в интервале температур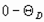 
, суммарная внутренняя энергия рассматривается как сумма функции температуры и функции удельного объема. Вместе с тем, ниже мы покажем, что такое рассмотрение внутренней энергии (или применение теории Дебая и Эйнштейна для определения изохорной теплоемкости) приводит к конфликту первого закона с третьим законом.
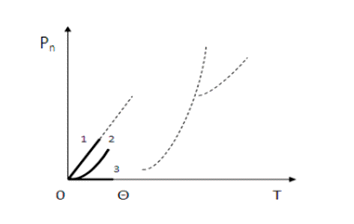
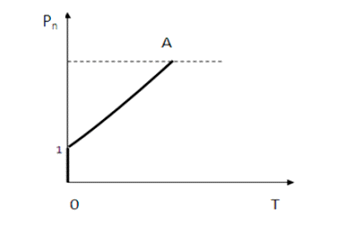
Рис. 2. Нагрев тела, изохорная теплоемкость которого зависит только от температуры. 1-с соблюдением первого закона. 2-с соблюдением третьего закона. 3-с соблюдением обеих законов.
В соответствии с (10) и (14) изохорная теплоемкость является функцией температуры (5) и твердые тела должны удовлетворять условие (6). Поэтому, если мы рассмотрим процесс нагрева тела в замкнутом объеме, то данный процесс, как минимум в данном интервале, в 
координатах должен выражаться прямой линией 1 ( Рис. 2. )
|
|
|
Покажем, что данный результат противоречит с третьим законом термодинамики.
Согласно данному закону “Приращение энтропии при абсолютном нуле температуры стремится к конечному пределу, не зависящему от того, в каком равновесном состоянии находится система”.
Иными словами, если температура равна абсолютному нулю, энтропия должна иметь одно и то же, (условно, нулевое) значение, независимо от других параметров состояния. Следовательно, изменения удельного объема и давления при постоянной, нулевой температуре не должны привести к изменениям энтропии. Изотермический процесс, при 
, одновременно является изоэнтропным. Для математического подтверждения сказанного можно использовать уравнение, которое получается из уравнения сохранения энергии с использованием уравнении Максвелла [1]
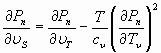, (15)
Из данного уравнения следует что при нулевой температуре
, (16)
Как видим, при нулевой температуре, закономерность изотермического изменения объема и давления не отличается от изоэнтропного (или адиабатического). Сказанное означает, что при 
, процесс изменения объема и давления, может происходит в условиях тепловой изоляции (т. е. без изменения энтропии) и:
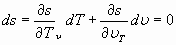, (17)
Прежде чем продолжим анализ данного вопроса, следует остановится на странность этого результата. Если мы имеем тело с нулевой температурой, процесс его изолированного сжатия или расширения должен менять только нетепловую составляющую его внутренней энергии т. е. потенциал межмолекулярных взаимодействии, не затрагивая температуру и тепловую составляющую внутренней энергии. Такую картину вполне можно представить при умеренных изменениях объема и давления. Но представьте себе, что адиабатическое сжатие происходит настолько сильно, что громадное тело принимает крошечные размеры а температура ничуть не повышается. Несмотря на то, что такой эксперимент никто не проводил, трудно представить, что при затратах огромной энергии на сжатие, температура тела останется опять равной нулю. Уже данный мысленный эксперимент позволяет думать, что, несмотря на всю строгость обоснования законов термодинамики, судить об их ограниченности вполне возможно.
|
|
|
А теперь покажем их очевидный конфликт. Из (17) следует:
. (18)
Путем преобразования исходного уравнения (1) методами математического анализа [1] легко можно заключить, что справедливы выражения
, 
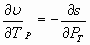. (19)
и, при нулевой температуре
, (20)
(Подробный вывод аналогичных соотношении можно смотреть и ниже)
Таким образом, согласно (6), линия изохорного нагрева должна быть прямой, а согласно (20) горизонтальной линией (линия 3 на рис. 2) и, в довольно широком диапазоне, изохорное повышение температуры тела не должно сопровождаться повышением давления, что, очевидно, не может наблюдаться в реальных условиях. Отмеченное означает, что уравнения (6) и (20), как следствия первого и третьего законов, не могут соблюдаться одновременно, что свидетельствует о наличии явного конфликта между данными законами. По всей видимости, реальный процесс изохорного нагрева должен выражаться линией 2, но такая зависимость отрицает принятую однозначную связь теплоемкости и температуры (9), (10) и требуется поставить под сомнением теории Дебая и Эйнштейна.
Как видим, возникает ощущение, что по мере приближения к абсолютному нулю, модель совокупности колеблющихся осцилляторов не совсем удачно отражает реальную картину процессов. Однако, такие сомнения могли бы иметь прочную основу, если бы внутри тела не существовал никакой другой источник (или резервуар) энергии. Но, если вакуум можно считать в качестве такого резервуара и его виртуальная энергия вполне может материализоваться, то ситуация резко меняется. Поэтому классические выражения для теплоемкости можно считать корректными, а наблюдаемые в окрестности критических температур разногласия, по всей видимости, можно объяснить тем, что в таких областях активизируются, материализуются энергетические резервуары нематериальной (квантовой и полевой) природы.
|
|
|
Учеными обнаружено, что, при низких температурах, сильное магнитное поле изменяет свойства веществ. Считают, что вблизи Т = 0 К, из-за уменьшения колебательной части теплоёмкости твердого тела, проявляются другие (не колебательные), низко расположенные уровни энергии твердого тела. Так, в металлах, при
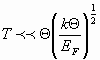, (21)
( 
— энергия Ферми) основной вклад в теплоёмкость вносят электроны проводимости (электронная часть теплоёмкости ~ Т), а в ферритах — спиновые волны (магнонная часть теплоёмкости ~ T, ). Квантовое " замораживание" большинства движений в твердых телах, вблизи 0 К позволяет измерить ядерную теплоёмкость и теплоёмкость, обусловленную локальными колебаниями квантового поля.
Известно что, характер изменения термодинамических параметров дополнительно усложняется фазовыми переходами, которые сопровождаются резким изменением многих величин, особенно, теплоёмкости.
Ниже мы покажем, что если изохорная теплоемкость является однозначной функцией температуры (внутренняя энергия выражается как сумма функции температуры и функции плотности), то энергия вакуума должна принимать участие в термодинамических процессах.
Допустим, что суммарная внутренняя энергия тела включает не только энергию теплового 
и электростатического (Ван-Дер-Ваальсового) происхождения 
, но и виртуальную энергию поля или вакуума, которая, (или определенная часть которой -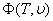 
) меняя свою величину в зависимости от состояния тела, способна приобрести сущность материальной энергии.
. (22)
Изменение такой суммарной внутренней энергии может происходить только за счет внешнего энергетического (теплового 
и механического 
) воздействия. Поэтому уравнение сохранения энергии принимает вид
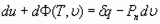. (23)
|
|
|
