 |
Для нашего примера эмпирическое корреляционное отношение 3 глава
|
|
|
|
Р и с. 2.2. Кумулята распределения 200 рабочих по размеру
заработной платы (графическое определение медианы)
Пользуясь кумулятой, можно определить значение признака у любой единицы ранжированного ряда.
Для симметричных распределений характерно совпадение значений средней арифметической, моды и медианы. Если М 0 > 
, то ряд будет иметь левостороннюю асимметрию (вытянутость), а если М 0 < 
, – правостороннюю асимметрию. В умеренно асимметричных рядах соотношение между указанными показателями выражается следующим образом:
| М 0 – | ≤ 3 ≤| Ме – |. (2.17)
В системе структурных показателей, определяющих особенности формы распределения, выступают варианты, занимающие определенное место (каждое четвертое, десятое, сотое и т.д.) в ранжированном вариационном ряду. Это квартили, децили, перцентели и др.
Квартили представляют собой значение признака, делящее ранжированную совокупность на четыре равновеликие части. Различают квартиль нижний (Q1), отделяющий ¼ часть совокупности с наименьшими значениями признака, и квартиль верхний (Q3), отсекающий ¼ часть с наибольшими значениями признака. Это означает, что 25% единиц совокупности будут меньше Q1; 25% единиц будут заключены между Q1 и Q2; 25% – между Q2 и Q3 и остальные 25% превзойдут Q3.
Вторая квартиль является медианой.
Квартили в дискретном вариационном ряду определяются аналогично вычислению медианы.
Для расчета квартилей по интервальному вариационному ряду используются формулы
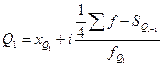; (2.18)
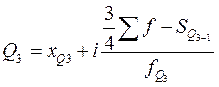, (2.19)
где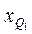 
– нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25%);
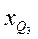– нижняя граница интервала, содержащего верхний квартиль (интервал определяется по накопленной частоте, первой превышающей 75%);
|
|
|
i – величина интервала;
– накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль;
– то же для верхнего квартиля;
– частота интервала, содержащего нижний квартиль;
– то же для верхнего квартиля.
Пример 2.15
Рассчитайте нижний и верхний квартили по данным, характеризующим коммерческие банки по срокам их функционирования (табл. 2.16).
Таблица 2.16
Распределение коммерческих банков по сроку функционирования
(на начало года)
| Группы банков по сроку функционирования, лет, x | Число банков, % к итогу, f | Накопленная частота, S |
| 1-2 2-3 3-4 4-5 5-6 6-7 7-8 Свыше 8 | ||
| Итого | 100,0 | - |
Решение
Определим номер Q для 1-го и 3-го квартилей:
;
.
Применяя способ расчета, аналогичный расчету медианы по ряду накопленных частот, определим, что
3<Q1<4, т.е. 
года;
5<Q1<6, т.е. 
года.
Итак, 25% банков имеют срок функционирования менее 3 лет, 25% банков – свыше 3 лет, а остальные имеют срок функционирования в пределах от 3 до 5,3 года.
Децили (d1) – это значения вариант, которые делят ранжированный ряд на десять равных частей: 1-й дециль (d1) делит совокупность в соотношении 1/10 к 9/10, 2-й дециль (d2) – в соотношении 2/10 к 8/10 и т.д.
Вычисляются децили по той же схеме, что и медиана, и квартили:
; (2.20)
; (2.21)
………………………….
. (2.22)
Пример 2.16
Продолжим пример с распределением коммерческих банков по сроку функционирования (см. табл. 2.16). Рассчитаем 1-й и 9-й децили.
Определим номер для 1-го и 9-го децилей:
,
.
По ряду накопленных частот определяем, что
2< d 1<3 т.е. 
года.
Это означает, что 10% коммерческих банков имеют срок функционирования менее 2 лет, а 90% банков имеют срок функционирования свыше 2 лет.
7< d 9<8 т.е. 
года.
Это означает, что 90% банков имеют срок функционирования меньше 7 лет, а 10% банков имеют срок функционирования свыше 7 лет.
Показатели дифференциации. В тех случаях, когда при изучении вариационного ряда возникает необходимость дать относительную характеристику степени вариации ряда и имеются уже предварительно вычисленные квартили и децили, то можно рассчитать коэффициент дифференциации (К д).
|
|
|
В зависимости от заданных ранговых показателей коэффициенты дифференциации рассчитываются по-разному.
1. Если заданы 3-я (Q 3) и 1-я (Q 1) квартили, то можно вычислить коэффициент дифференциации по формуле
. (2.23)
В большинстве случаев коэффициент вариации (V) составляет примерно 1,5 коэффициента дифференциации (К д), т.е.
V =1,5 K Д. (2.24)
Пример 2.17
По данным табл. 2.16, характеризующим коммерческие банки по сроку функционирования, имеем:
года, 
года, Q 1=3 года, Q 3=5,3 года.
Отсюда
раза, или 27,7%;
V =0,2771*1,5=0,416*100=41,6%≈42%,
что и требовалось доказать.
2. Если сопоставляются 9-я (d 9) и 1-я (d 1) децили, то децильный коэффициент дифференциации (КД) вычисляется по формуле
. (2.25)
Пример 2.18
По данным, представленным в табл. 2.16, d 1=2 года; d 9=7 лет; отсюда Кd =7/2=3,5 раза, т.е. минимальная величина срока функционирования 10% самых старых банков отличается от максимальной величины срока функционирования 10% самых молодых банков в 3,5 раза.
Рассмотренный выше показатель дифференциации не совсем точно измеряет уровень дифференциации, так как сопоставляется минимальная величина признака (25% или 10% самых крупных единиц совокупности) с максимальной величиной признака (25% или 10% самых мелких единиц совокупности).
3. Более точно уровень дифференциации можно измерить, сопоставив средние уровни, полученные из 10% наибольших и наименьших значений признака в совокупности. Такой показатель называется коэффициентом фондовой дифференциации (К ф):
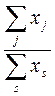, (2.26)
где 
– сумма значений признака 10% самых крупных единиц в совокупности;
n – число самых крупных и мелких единиц в совокупности;
– сумма значений признака 10% самых мелких единиц в совокупности.
Пример 2.19
Рассчитаем фондовый коэффициент. Имеются данные о размере капитала 20 коммерческих банков за год, млн руб.: 6,9; 9,3; 1,3; 6,0; 13,4; 3,7; 5,1; 2,9; 1,4; 1,6; 10,9; 7,2; 3,2; 8,9; 1,2; 8,2; 2,1; 8,1; 2,1; 11,5.
Так как 10% самых крупных и 10% самых мелких банков составляют одну и ту же величину (в нашем примере 1/10*20=2 ед.), то для расчета фондового коэффициента подставим в формулу (2.26) соответствующие значения и получим
|
|
|
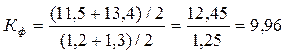раза.
Рассчитанный коэффициент показывает, что уровень дифференциации 20 коммерческих банков по размеру капитала достаточно высок; средний размер капитала 10% самых крупных банков в 9,96 раза превышает средний размер капитала 10% самых мелких банков.
2.2.2. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задача 2.14
Доходы пяти банков по операциям с ценными бумагами за отчетный период составили 0,4; 0,7; 0,8; 1,1; 1,2 ден. единиц.
Определите средний доход банка по данной операции.
Задача 2.15
Имеются данные страховых организаций области о числе заключенных договоров по личному добровольному страхованию (табл. 2.17).
Таблица 2.17
| № группы | Число договоров, тыс. х | Число страховых организаций f | Удельный вес страховых организаций, % d |
| I II III IV V | |||
| Итого |
Определите среднее число заключенных договоров в расчете на одну страховую организацию области.
Задача 2.16
По данным выборочного наблюдения имеется следующее распределение фермерских хозяйств района по размерам угодий (табл. 2.18).
Таблица 2.18
| № группы | Хозяйства по размерам угодий, га х | Число хозяйств f |
| I II III IV V | До 40 40-50 50-60 60-70 Свыше 70 | |
| Итого |
Определите средний размер угодья на одно фермерское хозяйство по району.
Задача 2.17
О показателях работы предприятий отрасли за отчетный период имеются следующие данные (табл. 2.19).
Таблица 2.19
| Показатель | № предприятия | ||||
| Объем продукции, тыс. шт. Стоимость реализованной продукции, тыс. руб. Прибыль, тыс. руб. | 9,0 | 9,8 | 8,5 | 8,6 | 9,1 |
Определите средние уровни каждого показателя по предприятиям отрасли.
Задача 2.18
Имеются следующие данные о продаже картофеля на рынках города (табл. 2.20).
Таблица 2.20
| № рынка | Средняя цена, руб. | Продано, тыс. кг. | Удельный вес продажи, % | ||
| Март | Май | Март | Май | ||
| 3,5 3,0 2,5 |
Определите средние цены картофеля по трем рынкам города в марте и мае, используя в качестве частот:
а) абсолютные данные о продаже товара,
|
|
|
б) удельные веса продажи товара.
Объясните, почему при неизменных ценах и общем объеме продажи средняя цена в мае изменилась.
Задача 2.19
Имеются группы предприятий, дифференцированные по темпам сокращения промышленного производства (табл. 2.21).
Таблица 2.21
| Сокращение производства, % | До 15 | 15-25 | 25-35 | 35-45 | свыше 45 |
| Число предприятий |
Определите средний процент сокращения промышленного производства по совокупности предприятий.
Задача 2.20
За отчетный период по пяти малым предприятиям отрасли имеются следующие данные (табл. 2.22).
Таблица 2.22
| Показатель | № предприятия | ||||
| Среднесписочная численность работников, чел. Средняя заработная плата, руб. |
Определите среднюю заработную плату работников предприятий отрасли.
Задача 2.21
Распределение предприятий региона по размеру прибыли характеризуется следующими данными (табл. 2.23).
Таблица 2.23
| Балансовая прибыль, млн руб. | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | Свыше 60 |
| Удельный вес предприятий, % |
Определите среднюю прибыль предприятия.
Задача 2.22
Имеются данные о финансовых показателях фирм, тыс. руб. (табл. 2.24).
Таблица 2.24
| № фирмы | Получено прибыли | Акционерный капитал | Рентабельность акционерного капитала, % | Удельный вес акционерного капитала, % |
| А | ||||
Определите средний процент рентабельности акционерного капитала фирм, используя показатели: а) гр. 1 и 2; б) гр. 2 и 3; в) гр. 1 и 3; г) гр. 3 и 4.
Задача 2.23
Имеются следующие данные об оплате труда работников малых предприятий (табл. 2.25).
Таблица 2.25
| № предприятия | Фонд заработной платы, руб. | Средне-списочная численность работников, чел. | Средне-месячная заработная плата, руб. | Удельный вес работников, % |
| А | ||||
| 270 000 240 000 |
Определите среднюю заработную плату работников предприятия, используя показатели: а) гр. 1 и 2; б) гр. 2 и 3; в) гр. 1 и 3; г) гр. 3 и 4.
Задача 2.24
По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города (табл. 2.26).
Таблица 2.26
| Размер вклада, руб. | До 400 | 400-600 | 600-800 | 800-1000 | свыше 1000 |
| Число вкладчиков |
Определите средний размер вклада.
Задача 2.25
По трем группам рабочих имеются следующие данные (табл. 2.27).
Таблица 2.27
| Число рабочих, n | Средняя заработная плата, руб. |
Рассчитайте среднюю заработную плату для всей совокупности рабочих.
Задача 2.26
Рассчитайте среднюю урожайность зерновых для всей группы хозяйств по следующим данным (табл. 2.28).
|
|
|
Таблица 2.28
| Урожайность зерновых, ц/га | Валовой сбор зерна, ц |
| 18 000 | |
| 30 000 | |
| 60 000 | |
| 44 000 | |
| 30 000 |
Задача 2.27
Определите среднюю выработку одного рабочего бригады по имеющимся данным (табл. 2.29).
Таблица 2.29
| Номер рабочего | |||||
| Произведено продукции за смену, шт. |
Задача 2.28
Имеется следующее распределение 60 рабочих по тарифному разряду (табл. 2.30).
Таблица 2.30
| Тарифный разряд | |||||
| Число рабочих |
Определите средний тарифный разряд рабочих.
Задача 2.29
Рабочие бригады имеют следующий стаж работы на предприятии (табл. 2.31).
Таблица 2.31
| Табельный номер рабочего | ||||||
| Стаж работы |
Определите средний стаж работы рабочих бригады.
Задача 2.30
Имеются данные о численности промышленно-производственного персонала (ППП) на предприятиях (табл. 2.32).
Таблица 2.32
| Численность ППП | Число предприятий |
| 291-602 | |
| 602-913 | |
| 913-1224 | |
| 1224-1535 |
Определите среднюю численность ППП, моду и медиану.
Задача 2.31
По данным задачи 2.26 определите 1-й и 3-й квартили предложенного ряда.
Задача 2.32
Распределение магазинов по размеру товарооборота характеризуется следующими данными (табл. 2.33).
Таблица 2.33
| Группа магазинов по размеру товарооборота, тыс. руб. | Число магазинов | Группы магазинов по размеру товарооборота, тыс. руб. | Число магазинов |
| До 200 | 500-600 | ||
| 200-300 | 600-700 | ||
| 300-400 | 700-800 | ||
| 400-500 | Свыше 800 |
Определите моду, медиану, квартили, децили и коэффициент дифференциации.
Задача 2.33
Имеются данные о размере 10 вкладов в банк в течение месяца в условных денежных единицах:
5,0; 7,4; 2,8; 10,1; 3,2; 4,5; 8,5; 3,0; 8,1; 11,5.
Рассчитайте фондовый коэффициент дифференциации.
Раздел 3. Показатели вариации
3.1. МЕТОДИЧЕСКИЕ УКАЗАНИЯ
И РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
Для измерения степени колеблемости отдельных значений признака от средней исчисляются основные обобщающие показатели вариации.
Размах вариации является наиболее простым измерителем вариации признака и определяется как разность между наибольшим и наименьшим значениями признака:
R = xmax – xmin. (3.1)
Среднее линейное отклонение представляет собой среднюю величину из отклонений вариантов признака от средней с учетом различия всех единиц совокупности:
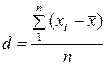– простое (для дискретного ряда значений признака), (3.2)
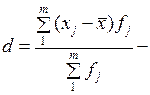взвешенное (для интервального ряда). (3.3)
Дисперсия 
– это средний квадрат отклонений, определяемый как средняя из отклонений, возведенных в квадрат.
– простая (для дискретного ряда); (3.4)
– взвешенная (для интервального ряда). (3.5)
Среднее квадратическое отклонение:
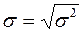. (3.6)
Коэффициент вариации – относительное среднее квадратическое отклонение, определяющее колеблемость признака:
(3.7)
Если 
>40%, это говорит о большой колеблемости признака.
Здесь:
xmax – максимальное значение признака;
xmin – минимальное значение признака;
n – число вариантов в дискретном ряду;
m – число интервалов в интервальном ряду;
xi – i -тое значение варьирующего признака (варианта);
xj – значение варьирующего признака в середине j -того интервала;
fj – частота.
По величине коэффициента вариации можно судить о степени вариации признаков, а следовательно, и об однородности состава совокупности. Чем больше его величина, тем больше разброс значений признака вокруг средней, тем менее однородна совокупность по составу.
Пример 3.1
Имеются выборочные данные о стаже работников коммерческих банков (табл. 3.1).
Определите:
1) средний стаж работников;
2) дисперсию;
3) среднее квадратическое отклонение;
4) коэффициент вариации.
Таблица 3.1
| Стаж, лет | Среднесписочная численность работников, чел. f | Середина интервала xi | xif | 
| 
| 
|
| До 3 | -3 | |||||
| 3 – 5 | -1 | |||||
| 5 – 7 | ||||||
| 7 – 9 | ||||||
| Свыше 9 | ||||||
| Итого | - | - | - |
Решение
1. Средний стаж работников по формуле (2.10)
тыс. руб.
2. Дисперсия по формуле (3.4)
.
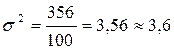3. Среднее квадратическое отклонение по формуле (3.6)
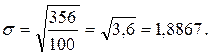
4. Коэффициент вариации по формуле (3.7)
.
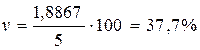Статистическую совокупность можно считать однородной по рассматриваемому признаку, если коэффициент вариации не превышает 33% [17].
Статистическое изучение вариации многих социально-экономических явлений проводится и при помощи дисперсии альтернативного признака. Обозначим наличие данного признака через 1, отсутствие – 0, долю вариантов, обладающих данным признаком, – p, а не обладающих им – q.
Дисперсия альтернативного признака 
, (3.8)
где 
; (3.9)
n – число наблюдений;
m – число единиц совокупности, обладающее данным признаком,
q = 1 – p. (3.10)
Пример 3.2
Определим дисперсию альтернативного признака по следующим данным: налоговой инспекцией одного из районов города проверено 172 коммерческих киоска и в 146 обнаружены финансовые нарушения. Тогда
п = 172, т = 146; 
; q = 1 – 0,85 = 0,15;
.
Наряду с изучением вариации признака по всей совокупности в целом часто бывает необходимо проследить количественные изменения признака по группам, на которые разделяется совокупность, а также между группами. Такое изучение вариации достигается посредством вычисления и анализа различных видов дисперсии.
Если данные представлены в виде аналитической группировки, то можно вычислить дисперсию общую, межгрупповую и внутригрупповую.
Общая дисперсия () измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию:
. (3.11)
Межгрупповая дисперсия (
) характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки. Она рассчитывается по формуле
(3.12)
где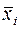 
и ni – соответственно групповые средние и численности по отдельным группам.
Внутригрупповая дисперсия 
отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она исчисляется следующим образом:
(3.13)
Средняя из внутригрупповых дисперсий 
:
. (3.14)
Существует закон, связывающий три вида дисперсии. Общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсии:
. (3.15)
Данное соотношение называют правилом сложения дисперсий. Согласно этому правилу общая дисперсия, возникающая под действием всех факторов, равна сумме дисперсии, появляющейся под влиянием всех прочих факторов, и дисперсии, возникающей за счет группировочного признака.
Зная любые два вида дисперсий, можно определить или проверить правильность расчета третьего вида.
Пример 3.3
Определим групповые дисперсии, среднюю из групповых дисперсий, межгрупповую дисперсию, общую дисперсию по данным табл. 3.2.
Таблица 3.2
Производительность труда двух бригад рабочих-токарей
| 1-я бригада | 2-я бригада | ||||||
| № п/п | Изготовлено деталей за час, шт. xi | xi – 
| (xi – ) 2
| № п/п | Изготовлено деталей за час, шт. xi | xi –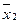 
| (xi – 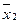) 2
|
| -2 -1 | -3 -2 -1 | ||||||
|
|
|
