 |
Для нашего примера эмпирическое корреляционное отношение 4 глава
|
|
|
|
Решение. Для расчета групповых дисперсий вычислим средние по каждой группе:
шт.; 
шт.
Промежуточные расчеты дисперсий по группам представлены в табл. 3.2. Подставив полученные значения в формулу (3.4), получим:
Средняя из групповых дисперсий
.
Затем рассчитаем межгрупповую дисперсию. Для этого предварительно определим общую среднюю как среднюю взвешенную из групповых средних:
шт.
Теперь определим межгрупповую дисперсию
.
Таким образом, общая дисперсия по правилу сложения дисперсий:
.
Проверим полученный результат, вычислив общую дисперсию обычным способом:
.
На основании правила сложения дисперсий можно определить показатель тесноты связи между группировочным (факторным) и результативным признаками. Он называется эмпирическим корреляционным отношением, обозначается 
(«эта») и рассчитывается по формуле
. (3.16)
Для нашего примера эмпирическое корреляционное отношение
.
Величина 0,86 характеризует существенную связь между группировочным и результативным признаками.
Величина 
называется коэффициентом детерминации и показывает долю межгрупповой дисперсии в общей дисперсии.
Наряду с вариацией количественных признаков может наблюдаться и вариация качественных признаков. Такое изучение вариации достигается, как и для долей количественных признаков, посредством вычисления и анализа следующих видов дисперсий.
Внутригрупповая дисперсия доли определяется по формуле
. (3.17)
Средняя из внутригрупповых дисперсий рассчитывается как
. (3.18)
Формула межгрупповой дисперсии имеет следующий вид:
, (3.19)
где ni – численность единиц в отдельных группах;
– доля изучаемого признака во всей совокупности, которая определяется по формуле
|
|
|
. (3.20)
Общая дисперсия имеет вид
. (3.21)
Три вида дисперсии связаны между собой следующим образом:
. (3.22)
Пример 3.4
Определим групповые дисперсии, среднюю из групповых, межгрупповую и общую дисперсии по данным табл. 3.3.
Таблица 3.3
Численность и удельный вес одной из категорий
крупного рогатого скота фермерских хозяйств района
| Хозяйство | Удельный вес дойных коров, % pi | Всего коров ni |
| Итого |
Решение
Определим долю дойных коров в целом по трем хозяйствам:
;
.
Общая дисперсия доли дойных коров:
.
Внутригрупповые дисперсии:
; 
; 
.
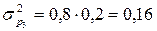Средняя из внутригрупповых дисперсий:
.
Межгрупповая дисперсия:
.
Используя правило сложения дисперсий, получаем: 0,1025+0,0031=0,1056. Пример решен правильно.
Пример 3.5
По данным выборочного обследования заработной платы работников бюджетной сферы получены следующие показатели (табл. 3.4).
Таблица 3.4
| Отрасль | Средняя заработная плата, руб. xi | Численность работников, чел. fj | Дисперсия заработной платы σ i2 |
| Здравоохранение | |||
| Образование |
Определите:
1) среднюю заработную плату по двум отраслям;
2) дисперсии заработной платы:
а) среднюю из групповых дисперсий (отраслевых),
б) межгрупповую (межотраслевую),
в) общую;
3) коэффициент детерминации;
4) эмпирическое корреляционное отношение.
Решение
1. Средняя заработная плата работников по двум отраслям рассчитывается по формуле (2.10):
руб.
2. Дисперсии заработной платы:
а) средняя из групповых дисперсий по (3.14)
;
б) межгрупповая дисперсия согласно (3.12)
.
в) общая дисперсия, полученная на основании правила сложения дисперсий (3.15):
.
3. Коэффициент детерминации равен величине
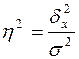; (3.23)
т.е. 
, или 44,24%.
Он показывает, что оплата труда на 44,24% зависит от отраслевой принадлежности работников и на 55,76% – от внутриотраслевых причин.
По формуле (3.16) эмпирическое корреляционное отношение 
,
|
|
|
что свидетельствует о существенном влиянии на дифференциацию заработной платы отраслевых особенностей.
3.2. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задача 3.1
По распределению 60 рабочих по тарифному разряду имеются следующие данные (табл. 3.5).
Таблица 3.5
| Тарифный разряд (x) | |||||
| Число рабочих (f) |
Определите:
1) средний тарифный разряд рабочих;
2) среднее линейное отклонение;
3) дисперсию;
4) среднее квадратическое отклонение;
5) коэффициент вариации.
Задача 3.2
По результатам экзаменационной сессии 1 и 2 курсов одного из вузов имеются следующие данные: на 1 курсе сдали сессию без двоек 85% студентов, на 2 курсе – 90%.
Определите на каждом курсе дисперсию доли студентов, успешно сдавших сессию.
Задача 3.3
Акционерные общества области по среднесписочной численности работающих на 1 января 2004 г. распределились следующим образом (табл. 3.6).
Таблица 3.6
| Группы АО по численности работающих | до 400 | 400-600 | 600-800 | 800-1000 | 1000-1200 | 1200-1400 | 1400-1600 | 1600-1800 |
| Количество АО |
Рассчитайте:
1) среднее линейное отклонение;
2) дисперсию;
3) среднее квадратическое отклонение;
4) коэффициент вариации.
Задача 3.4
Имеются данные о распределении семей сотрудников предприятия по количеству детей (табл. 3.7).
Таблица 3.7
| Число детей в семье | Число семей сотрудников по подразделениям | ||
| первое | второе | третье | |
| - |
Вычислите:
1) внутригрупповые дисперсии;
2) среднюю из внутригрупповых дисперсий;
3) межгрупповую дисперсию;
4) общую дисперсию.
Проверьте правильность проведенных расчетов с помощью правила сложения дисперсий.
Задача 3.5
Распределение стоимости продукции, предназначенной для экспорта по цехам предприятия, представлено следующими данными (табл. 3.8).
Таблица 3.8
| Цех | Стоимость всей произведенной продукции (тыс. руб.) | В том числе стоимость экспортной продукции (тыс. руб.) |
| Итого |
Вычислите:
1) среднюю из внутригрупповых, межгрупповую и общую доли экспортной продукции;
2) коэффициент детерминации и эмпирическое корреляционное соотношение.
Задача 3.6
По данным обследования коммерческих банков города, 70% общего числа клиентов составили юридические лица со средним размером кредита 120 тыс. руб. и коэффициентом вариации 25%, а 20% – физические лица со средним размером ссуды 20 тыс. руб. при среднем квадратическом отклонении 6 тыс. руб.
|
|
|
Используя правила сложения дисперсий, определите тесноту связи между размером кредита и типом клиента, исчислив эмпирическое корреляционное отношение.
Раздел 4. Выборочное наблюдение
4.1. МЕТОДИЧЕСКИЕ УКАЗАНИЯ
И РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
Целью выборочного наблюдения является определение характеристик генеральной совокупности – генеральной средней (
о) и генеральной доли (р). Характеристики выборочной совокупности – выборочная средняя (
) и выборочная доля (
) отличаются от генеральных характеристик на величину ошибки выборки (
). Поэтому для определения характеристик генеральной совокупности необходимо вычислять ошибку выборки, или ошибку репрезентативности, которая определяется по формулам, разработанным в теории вероятностей для каждого вида выборки и способа отбора.
Собственно случайная и механическая выборки. При случайном повторном отборе предельная ошибка выборки для средней () и для доли () рассчитывается по формулам
; (4.1)
(4.2)
где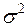 
– дисперсия выборочной совокупности;
n – численность выборки;
t – коэффициент доверия, который определяется по таблице значений интегральной функции Лапласа при заданной вероятности (Pдов.) (табл. П1).
При бесповторном случайном и механическом отборе предельная ошибка выборки вычисляется по формулам
; (4.3)
, (4.4)
где N – численность генеральной совокупности.
Пример 4.1
Для определения зольности угля в месторождении в порядке случайной выборки было обследовано 100 проб угля. В результате обследования установлено, что средняя зольность угля в выборке составляет 16%, среднее квадратическое отклонение – 5%. В десяти пробах зольность угля составила более 20%. С вероятностью 0,954 определите пределы, в которых будут находиться средняя зольность угля в месторождении и доля угля с зольностью более 20%.
Решение
|
|
|
Средняя зольность угля будет находиться в пределах
Для определения границ генеральной средней вычислим предельную ошибку выборки для средней по формуле (4.1):
. (4.5)
С вероятностью 0,954 можно утверждать, что средняя зольность угля в месторождении будет находиться в пределах 16% 
1%, или 15% 
17%.
Доля угля с зольностью более 20% будет находиться в пределах
.
Выборочная доля определяется по формуле
, (4.6)
где m – доля единиц, обладающих признаком
Ошибку выборки для доли (
) вычислим по формуле (4.2):
или ±6%.
С вероятностью 0,954 можно утверждать, что доля угля с зольностью более 20% в месторождении будет находиться в пределах 
, или 
.
Пример 4.2
Для определения среднего срока пользования краткосрочным кредитом в банке была произведена 5%-ная механическая выборка, в которую попало 100 счетов. В результате обследования установлено, что средний срок пользования краткосрочным кредитом – 30 дней при среднем квадратическом отклонении 9 дней. В пяти счетах срок пользования кредитом превышал 60 дней. С вероятностью 0,954 определите пределы, в которых будут находиться срок пользования краткосрочным кредитом в генеральной совокупности и доля счетов со сроком пользования краткосрочным кредитом более 60 дней.
Решение
Средний срок пользования кредитом в банке находится в пределах
.
Так как выборка механическая, то ошибка выборки определяется по формуле (2.3):
дня.
С вероятностью 0,954 можно утверждать, что срок пользования краткосрочным кредитом в банке находится в пределах 
=30 дней 
2 дня, или
28 дней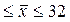 
дня.
Доля кредитов со сроком пользования более 60 дней находится в пределах
.
Выборочная доля составит
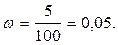
Ошибку выборки для доли определим по формуле (4.4):
или 4,2%.
С вероятностью 0,954 можно утверждать, что доля кредитов в банке со сроком пользования более 60 дней будет находиться в пределах 
или 
Типическая выборка. При типическом (районированном) отборе генеральная совокупность разбивается на однородные типические группы, районы. Отбор единиц наблюдения в выборочную совокупность производится различными методами. Рассмотрим типическую выборку с пропорциональным отбором внутри типических групп.
Объем выборки из типической группы при отборе, пропорциональном численности типических групп, определяется по формуле
(4.7)
где ni – объем выборки из типической группы;
Ni – объем типической группы.
Предельная ошибка выборочной средней и доли при бесповторном случайном и механическом способе отбора внутри типических групп рассчитывается по формулам
; (4.8)
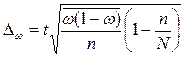, (4.9)
где 
– дисперсия выборочной совокупности.
Пример 4.3
Для определения среднего возраста мужчин, вступающих в брак, в районе была произведена 5%-ная типическая выборка с отбором единиц пропорционально численности типических групп. Внутри групп применялся механический отбор. Данные сведены в табл. 4.1.
|
|
|
Таблица 4.1
| Социальная группа | Число мужчин | Средний возраст | Среднее квадратическое отклонение | Доля мужчин, вступающих во второй брак, % |
| Рабочие | ||||
| Служащие |
С вероятностью 0,954 определите пределы, в которых будет находиться средний возраст мужчин, вступающих в брак, и долю мужчин, вступающих в брак во второй раз.
Решение
Средний возраст вступления мужчин в брак находится в пределах
.
Средний возраст вступления мужчин в брак в выборочной совокупности определим по формуле средней взвешенной
(4.10)
= 
года.
Средняя выборочная дисперсия определяется по формуле
средней
; (4.11)
= 
Предельную ошибку выборки вычислим по формуле (4.8):
года.
С вероятностью 0,954 можно утверждать, что средний возраст мужчин, вступающих в брак, будет находиться в пределах 
года 
года, или
24 года 
года.
Доля мужчин, вступающих в брак во второй раз, будет находиться в пределах
.
Выборочную долю определим по формуле средней
или 14%.
Среднюю выборочную дисперсию альтернативного признака вычисляем по формуле
(4.12)
Ошибку выборки для доли определим по формуле (4.9):
или 6%.
С вероятностью 0,954 можно утверждать, что доля мужчин, вступающих в брак во второй раз, будет находиться в пределах 
, или 
.
Серийная выборка. При серийном способе отбора генеральную совокупность делят на одинаковые по объему группы – серии. В выборочную совокупность отбираются серии. Внутри серий производится сплошное наблюдение единиц, попавших в серию.
При бесповторном отборе серий предельные ошибки выборочной средней и доли определяются по формуле
, (4.13)
где 
– межсерийная дисперсия;
R – число серий в генеральной совокупности;
r – число отобранных серий.
Пример 4.4
В цехе предприятия 10 бригад рабочих. С целью изучения их производительности труда была осуществлена 20%-ная серийная выборка, в которую попали 2 бригады. В результате обследования установлено, что средняя выработка рабочих в бригадах составила 4,6 и 3 т. С вероятностью 0,997 определите пределы, в которых будет находиться средняя выработка рабочих цеха.
Решение
Средняя выработка рабочих цеха будет находиться в пределах
.
Выборочную среднюю серийной выборки определим по формуле (2.1):
т.
Дисперсию серийной выборки определим из выражения
, (4.14)
где 
– выборочная средняя серии;
– выборочная средняя серийной выборки.
Значение дисперсии составляет величину
.
Рассчитаем предельную ошибку выборки для средней по формуле (4.13):
т.
С вероятностью 0,997 можно утверждать, что средняя выработка рабочих цеха находится в пределах 
т 
т, или 
т.
Пример 4.5
На складе готовой продукции цеха находятся 200 ящиков деталей по 40 штук в каждом ящике. Для проверки качества готовой продукции была произведена 10%-ная серийная выборка. В результате выборки установлено, что доля бракованных деталей составляет 15%. Дисперсия серийной выборки равна 0,0049.
С вероятностью 0,997 определите пределы, в которых находится доля бракованной продукции в партии ящиков.
Решение
Доля бракованных деталей будет находиться в пределах
.
Определим предельную ошибку выборки для доли по формуле (4.13):
или 4,4%.
С вероятностью 0,997 можно утверждать, что доля бракованных деталей в партии находится в пределах 10,6% 
19,6%.
Пример 4.6
В области, состоящей из 20 районов, проводилось выборочное обследование урожайности на основе отбора серий (районов). Выборочные средние по районам составили соответственно 14,5 ц/га; 16; 15,5; 15 и 14 ц/га. С вероятностью 0,954 найдите пределы урожайности во всей области.
Решение
Рассчитаем общую среднюю:
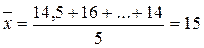ц/га.
Межгрупповая (межсерийная) дисперсия
.
Определим теперь предельную ошибку серийной бесповторной выборки (t = 2, Рдов = 0,954) по формуле (4.13):
.
Следовательно, урожайность в области (с вероятностью 0,954) будет находиться в пределах
15-1,7≤ 
≤15+1,7,
или
13,3 ц/га≤ 
≤16,7 ц/га.
В практике проектирования выборочного наблюдения возникает потребность в нахождении численности выборки, которая необходима для обеспечения определенной точности расчета генеральных характеристик – средней и доли. При этом предельная ошибка выборки, вероятность ее появления и вариация признака предварительно известны.
При случайном повторном отборе численность выборки определяется из выражения
. (4.15)
При случайном бесповторном и механическом отборе численность выборки вычисляется по формуле
. (4.16)
Для типической выборки
. (4.17)
Для серийной выборки
. (4.18)
Пример 4.7
В районе проживает 2000 семей. Предполагается провести их выборочное обследование методом случайного бесповторного отбора для нахождения среднего размера семьи. Определите необходимую численность выборки при условии, что с вероятностью 0,954 ошибка выборки не превысит одного человека при среднем квадратическом отклонении, составляющем три человека (
=3).
Решение
При бесповторном случайном отборе численность выборки по формуле (4.16) составит 
семей.
Численность выборки: не менее 36 семей.
Пример 4.8
В городе А проживает 10 000 семей. С помощью механической выборки предполагается определить долю семей с тремя детьми и более. Какова должна быть численность выборки, чтобы с вероятностью 0,954 ошибка выборки не превышала 0,02, если на основе предыдущих обследований известно, что дисперсия равна 0,2?
Решение
Определим необходимую численность выборки по формуле (4.16):
.
Численность выборки: не менее 1667.
В статистике часто приходится сравнивать результаты двух (или более) выборок. На основании сравнения двух выборочных средних (или долей) делается вывод о случайности или существенности их расхождения.
Для этого абсолютная разность показателей выборочных средних 
сопоставляется со средней ошибкой разности 
:
. (4.19)
Найденное t расч. сравнивается с t табл. по t – распределению Стьюдента (таблица П2) для числа степеней свободы v = n 1+ n 2-2 и заданного уровня значимости a. (здесь n 1 и n 2 – объемы сравниваемых выборок).
|
|
|
