Для нашего примера эмпирическое корреляционное отношение 7 глава

для цепных индексов – ; ; … . (6.28)

Если известны цепные индексы, то путем их последовательного перемножения можно получить базисные индексы.

Пример 6.10

Рост цен на молоко в магазине характеризуется следующими данными (табл. 6.6).

Таблица 6.6

Месяц 2005 г.	Январь	Февраль	Март
Цена, % к предыдущему периоду	100,8	103,5	98,7

 

Определите общее изменение цен за квартал.

Решение

Цепные индексы цен: i _я= =1,008;

i _ф= 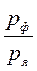=1,035;

i_м = = 0,987.

Общее изменение цен определяются по формуле (6.28):

I_p = =1,008*1,035*0,987=1,029.

Следовательно, за 1-й квартал 2005 г. цены на молоко выросли на 2,9%.

6.2. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

Задача 6.1

Реализация плодово-ягодной продукции в области отражена в табл. 6.7.

Таблица 6.7

Наименование товара	Июль	Август	Расчетные графы, руб.
Цена за 1 кг, руб. Р0	Продано Т q0	Цена за 1 кг, руб. Р1	Продано Т q1	p0q0	p1q1	p0q1
Черешня Персики Виноград
Итого	x	x	x	x

 

Рассчитайте индекс товарооборота.

Задача 6.2

Рассчитайте индекс сезонности и постройте график на основе данных табл. 6.8.

Таблица 6.8

Месяц	Реализация
2004 г.	2005 г.	2006 г.
А
Январь
Февраль
Март
Апрель
Май
Июнь
Июль
Август
Сентябрь
Октябрь
Ноябрь
Декабрь
Итого

 

Задача 6.3

Трудоемкость и выпуск продукции на предприятии представлены в табл. 6.9.

Таблица 6.9

Вид продукции	Затраты времени на 1 изделие, чел.-ч	Произведено шт.	Расчетные графы, чел.-ч
Январь t0	Февраль t1	Январь q0	Февраль q1	t0 q1	t1 q1
Изделие А Изделие Б Изделие В	1,0 1,2 0,9	0,9 1,0 0,8			450,0 388,8 676,8	405,0 324,0 601,6
Итого					1515,6	1330,6

 

Рассчитайте сводный индекс производительности труда по трудоемкости.

Задача 6.4

По имеющимся данным табл. 6.10 вычислите индекс производительности труда.

Таблица 6.10

Вид продукции	Сентябрь	Октябрь	Отпускная цена, руб. p1	Расчетные графы, руб.
Произведено, шт. q0	Трудовые затраты, чел.-ч T0	Произведено, шт. q1	Трудовые затраты, чел.-ч T1	q0 p1	q1 q1 p1
Изделие А Изделие Б Изделие В
Итого

Задача 6.5

Реализация товара в натуральном и стоимостном выражения х отражена в табл. 6.11.

Таблица 6.11

Товар	Реализация в базисном периоде, руб. q0p0	Изменение физического объема реализации в текущем периоде по сравнению с базисным, %	Расчетные графы
	iq	iq q0p0
Мандарины Грейпфруты		-6,4 -8,2	0,936 0,918

Окончание табл. 6.11

 

Товар	Реализация в базисном периоде, руб. q0p0	Изменение физического объема реализации в текущем периоде по сравнению с базисным, %	Расчетные графы
	iq	iq q0p0
Апельсины		+1,3	1,013
Итого		х	х

 

Рассчитайте средний арифметический индекс реализации товара.

 

Задача 6.6

Вычислите индекс цен переменного состава (изменение цен от реализации товара А в двух регионах) по данным табл. 6.12.

Таблица 6.12

Регион	Июнь	Июль	Расчетные графы, руб.
Цена, руб. p0	Продажа, шт. q0	Цена, руб. p1	Продажа, шт. q1	p0 q0	p1 q1	p0 q1
Итого	х		х

Задача 6.7

Данные по товарообороту предприятия приведены в табл. 6.13.

Таблица 6.13

Товар	Продажа товара, тыс. кг	Средняя цена, кг, руб.
1995 г.	1996 г.	1995 г.	1996 г.
Морковь	15,0	16,2
Яблоки	50,0	51,0

 

Вычислите:

1) индивидуальные индексы цен и проданного товара;

2) общий индекс товарооборота;

3) общий индекс физического объема товарооборота;

4) общий индекс цен и сумму экономии или перерасхода от изменения цен;

5) прирост товарооборота за счет изменения цен и количества продаж товаров.

Задача 6.8

Денежные доходы увеличились в среднем на 15 %, а индекс потребительских цен составил 1,2. Найдите индекс реального дохода.

Задача 6.9

Предприятие производит продукцию нескольких наименований. Объем выпуска в действующих ценах за год вырос в 5 раз. Индекс физического объема продукции за этот же период составил 1,25. Как изменилась средняя цена продукции предприятия?

Задача 6.10

Предприятие выпускает фотоаппараты нескольких типов. Средняя цена фотоаппарата выросла за год на 100%. Индекс цен фиксированного состава равен 1,25. Как изменилась структура продукции? Как изменение структуры охарактеризовать количественно?

Задача 6.11

В отчетном периоде товарооборот в фактических ценах по сравнению с базисным вырос на 12%, а цены снизились на 3%. Как увеличился объем реализуемой продукции в отчетном периоде?

Задача 6.12

В отчетном периоде товарооборот в фактических ценах вырос на 7%, а физический объем реализуемой продукции увеличился на 10%. Как изменились цены в отчетном периоде по сравнению с базисным?

Задача 6.13

За некоторый период изменились цены двух потребительских товаров А и Б. Индекс цен товара А составил 1,5, а товара Б – 0,8. Цены остальных товаров не изменились. Найдите индекс потребительских цен, если известно, что в бюджете домашнего хозяйства расходы на товар А составили 15%, а на товар В – 12%.

Задача 6.14

Продажа товара в магазинах ассоциации представлена в табл. 6.14 в условных ценах.

Таблица 6.14

Магазин	Базисный период	Отчетный период
Количество товара	Цена за единицу продукции	Количество товара	Цена за единицу продукции
А
Б

 

Определите индексы цен:

1) переменного состава,

2) постоянного состава,

3) индекс структурных сдвигов.

Задача 6.15

Имеются следующие данные о выпуске продукции (табл. 6.15).

Таблица 6.15

Вид продукции	Произведено продукции в отчетном году	Себестоимость единицы продукции
Базисный год	Отчетный год
А
Б		2,8	2,5

 

Определите:

1) индивидуальный и общий индекс продукции;

2) сумму экономии (перерасхода) от изменения себестоимости продукции.

Задача 6.16

О продаже и ценах на продукты на одном из рынков города имеются следующие данные (табл. 6.16).

Таблица 6.16

Продукт	Единица измерения	Продано, тыс. ед.	Цена единицы, руб.
В базисном периоде q	В отчетном периоде q	В базисном периоде q	В отчетном периоде q
А	Л				2,5
Б	Кг				1,5
В	Кг	1,5

Определите:

1) общее изменение физического объема продаж;

2) общее изменение цен на указанные продукты;

3) абсолютную экономию населения от снижения цен.

Задача 6.17

Определите среднее снижение цен на швейные изделия в отчетном периоде по сравнению с базисным по следующим данным (табл. 6.17).

 

Таблица 6.17

Наименование швейных изделий	Снижение цен в отчетном периоде по сравнению с базисным, %	Продано в отчетном периоде, млн руб.
Хлопчатобумажные	-20
Капроновые	-15

Задача 6.18

О выпуске продукции мебельной фабрики имеются следующие данные (табл. 6.18).

Таблица 6.18

Наименование изделий	Изменение выпуска в мае по сравнению с апрелем, %	Выпуск продукции в апреле, млн руб., q0p0
Столы	+12
Диваны	+10
Стулья	+15

 

Определите увеличение выпуска всей продукции в мае по сравнению с апрелем (в %), т.е. рассчитайте общий индекс физического объема.

Задача 6.19

О динамике потребительских цен в РФ за 2004 г. имеются следующие данные (табл. 6.19).

Таблица 6.19

Группа товаров	Индекс потребительских цен (2004 г. по отношению к 2003 г.) в разах, i	Структура потребительских расходов в 2003 г. (по данным обследований семейных бюджетов), %
Продовольственные товары	3,1	49,4
Непродовольственные товары	2,9	43,1
Платные услуги	7,6	7,5

 

Рассчитайте сводный (общий) индекс потребительских цен.

Задача 6.20

Об изменении численности рабочих на заводе имеются следующие данные, % к предыдущему году (табл. 6.20).

Таблица 6.20

+5	+4	+7	+5	+6

 

Определите, на сколько процентов увеличилось число рабочих на заводе за 5 лет, т.е. в 1995 г. по сравнению с 1990 г.

Задача 6.21

О производстве и себестоимости продукта А по двум фабрикам за два периода имеются следующие данные (табл. 6.21).

Таблица 6.21

 

Фабрика	Произведено, тыс. ед.	Себестоимость единицы продукта, руб.
В базисном периоде q	В отчетном периоде q	В базисном периоде z	В отчетном периоде z
Всего			-	-

 

Определите:

1) изменение себестоимости продукта А по каждой фабрике;

2) изменение себестоимости в целом по обеим фабрикам с помощью индексов переменного и фиксированного составов;

3) индекс структуры.

Задача 6.22

Об урожайности и посевных площадях озимых зерновых культур в 1991 и 1995 гг. по РФ имеются следующие данные (табл. 6.22).

Определите:

1) общий индекс урожайности озимых зерновых культур:

а) переменного состава;

б) фиксированного состава;

2) индекс структурных сдвигов.

Таблица 6.22

Культура	Урожайность, ц/га	Посевная площадь, млн га	Валовой сбор, млн ц
Пшеница	28,1	16,9	9,2	8,2	258,52	138,58
Рожь	16,4	12,6	6,5	3,2	106,60	40,32
Ячмень	35,1	28,3	0,78	0,47	27,38	13,30
Всего	-	-	16,48	11,87	392,50	192,20

Задача 6.23

1. Чему будет равен индекс издержек на производство, если себестоимость увеличилась на 10%, а количество продукции снизилось на 8%?

2. Чему будет равен индекс физического объема продукции, если численность рабочих возросла на 12%, а производительность труда – на 7%?

Задача 6.24

Валовая добавленная стоимость базисного периода в сельском хозяйстве – 200 млн руб.; численность работников сельского хозяйства – 50 тыс. человек. В отчетном периоде численность работников снизилась на 2 тыс. человек, а их производительность труда выросла на 3 тыс. руб. Определите влияние факторов на рост валовой добавленной стоимости сельского хозяйства.

Задача 6.25

За изучаемый период общая сумма затрат на производство продукции увеличилась на 9,3%, а объем производства – на 13,4%. Определите изменение себестоимости единицы продукции.

Раздел 7. Статистические показатели связи

7.1. МЕТОДИЧЕСКИЕ УКАЗАНИЯ
И РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ

При статистическом исследовании корреляционных связей основной задачей является определение на основе регрессионного анализа их формы (математической модели связи) и тесноты связи.

Математическими моделями связи могут быть уравнения регрессии:

линейное – y = a₀ + a₁; (7.1)

степенное – y = a₀ x^a1; (7.2)

квадратичное – y = a₀ + a₁ x + a₂ x² и др. (7.3)

Для линейной модели её параметры определяются:

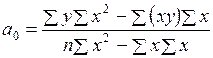; (7.4)

. (7.5)

Здесь параметр a₁ показывает изменение результативного признака (у) при изменении факторного признака (х) на единицу.

Теснота связи определяется коэффициентом корреляции r. При линейной форме связи он рассчитывается по формуле

. (7.6)

Показатели тесноты связи, исчисленные по данным сравнительно небольшой статистической совокупности, могут искажаться действием случайных причин. Это вызывает необходимость проверки их существенности.

Для оценки значимости коэффициента корреляции r применяется t- критерий Стьюдента. При этом фактическое значение критерия t_r:

(7.7)

Вычисленное по формуле (7.7) значение t_r сравнивается с критическим t_кр, которое берется из таблицы значений t Стьюдента с учетом заданного уровня значимости α и числа степеней свободы k.

Если t_r > t_кр, то величина коэффициента корреляции признается существенной.

Для получения выводов о практической значимости синтезированных моделей показателям тесноты связи дается качественная оценка. Это осуществляется на основе шкалы Чеддока, приведенной в табл. 7.1.

 

Таблица 7.1

Шкала Чеддока

Показатели тесноты связи	Характеристика силы связи
0,1 – 0,3	слабая
0,3 – 0,5	умеренная
0,5 – 0,7	заметная
0,7 – 0,9	высокая
0,9 – 0,99	весьма высокая

 

Чем сильнее связь, тем сильнее влияние изучаемого фактора на результативный признак у. При слабой связи вариация результативного признака определяется неучтенными факторами.

Часто исследуемые признаки имеют разные единицы измерения. Тогда для оценки влияния факторного признака на результативный применяются коэффициент эластичности (Э):

, (7.8)

где – первая производная уравнения регрессии.

Средний коэффициент эластичности определяется для линейного уравнения по формуле

. (7.9)

Он показывает, на сколько процентов изменяется результативный признак при изменении факторного признака на 1%.

Пример 7.1

Имеются выборочные данные по 10 однородным предприятиям (табл. 7.2).

Таблица 7.2

№ предприятия
Электровооруженность труда на 1 рабочего, кВт-ч
Выпуск готовой продукции на одного рабочего, т

 

Постройте однофакторную регрессионную модель и определите тесноту связи.

Решение

Примем, что факторным признаком (х) является электровооруженность труда, а результативным (у) – выпуск готовой продукции. Будем считать, что между ними существует линейная связь y = a₀ + a₁ x. Для вычисления параметров модели по формулам (7.4) и (7.5) представим в табл. 7.3 исходные данные и необходимые дополнительные расчетные значения.

Таблица 7.3

Расчет сумм для вычисления параметров уравнения прямой

Исходные данные	Расчетные значения
№ предприятия	х	у	ху	х2	у2

Окончание табл. 7.3

 

Исходные данные	Расчетные значения
№ предприятия	х	у	ху	х2	у2
…	…	…	…	…	…
Итого
В среднем	5,0	6,0	34,3	30,4	40,0

 

;

.

Линейная модель будет иметь вид

у = 2,02 + 0,796 х. (7.10)

Параметр а ₁ показывает, что с увеличением электровооруженности труда одного работника на 1 кВт-ч выпуск готовой продукции возрастет на 0,796 т.

Рассчитаем коэффициент корреляции по формуле (7.6):

Значение r показывает, что между энерговооруженностью труда и выпуском продукции существует сильная связь.

Средний коэффициент эластичности по формуле (7.9)

,

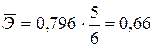т.е. с увеличением электровооруженности труда на 1% выпуск продукции возрастет на 0,66%.

Произведем оценку значимости коэффициента корреляции t по формуле (7.7):

.

С учетом принятых в экономико-статистических исследованиях величин значимости α =0,05 (Р_дов =0,95) и числа степеней свободы 10–2=8 табличное значение t_кр= 2,3.

Сравнивая t_расч. и t_кр , имеем, что t_расч > t_кр., поэтому коэффициент корреляции признается существенным, а синтезированная математическая модель (7.1) может быть использована для практических целей.

Определить, случайно или неслучайно предлагаемое в задачах распределения, т.е. сделать вывод о наличии или отсутствии зависимости между признаками, положенными в основу группировки, можно по критерию Пирсона ().

,

- эмпирические частоты в таблицах;

- теоретические частоты.

Пример 7.2

Имеются данные о распределении 600 студентов-вечерников по двум признакам: характеру работы и результатам сдачи экзаменов по специальным дисциплинам:

 

Характер работы	Сдавшие сессию без двоек	Получившие неудовлетворительные оценки	Всего студентов
Работающие по профилю
Работающие не по профилю специальности

 

Теоретические частоты рассчитываются по каждой строке:

; ;

,

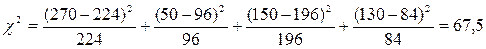Число степеней свободы (табл. Пирсона):

,

где , - число строк и столбцов.

По таблице Пирсона (прилож.П3) определяем табличное (пороговое) значение , допустимое при случайных расхождениях между эмпирическими () и теоретическими () частотами.

Примем или . При числе степеней свободы и по таблице Пирсона (см. Прилож.1) определяем =3,84.

Так как , делаем вывод, что распределение неслучайно, т.е. существует зависимость между характером работы студентов и результатами сдачи ими экзаменов по специальным дисциплинам.

При исследовании степени тесноты связи между качественными признаками, каждый из которых представлен в виде альтернативных признаков, возможно использование так называемых «тетрахорических показателей». Тогда расчетная таблица (табл. 7.4) состоит из четырех ячеек (обозначаемых буквами a, b, c, d). Каждая из клеток соответствует известной альтернативе того или другого признака.

Таблица 7.4

	Да	Нет
Да	a	b
Нет	c	d

 

Для такого рода таблиц построен ряд показателей: коэффициент ассоциации и коэффициент контингенции.

Коэффициент ассоциации К_а определяется по формуле

. (7.11)

Коэффициент контингенции К_к рассчитывается из выражения

. (7.12)

Связь считается подтвержденной, если К_а > 0,5 или К_к > 0,3.

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: