 |
Для нашего примера эмпирическое корреляционное отношение 5 глава
|
|
|
|
При n > 20 t табл обычно принимается равным 3.
Для n > 20 средняя ошибка разности определяется по формуле
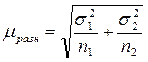. (4.20)
Для n < 20
. (4.21)
Здесь 
и 
– дисперсии сравниваемых выборок.
Если t расч.< t табл., расхождение можно считать случайным.
Пример 4.9
Предположим, на предприятии из коллектива рабочих выборочно обследовано 25 мужчин и 25 женщин. Среднемесячная заработная плата мужчин оказалась равна 2830 руб. при среднем квадратическом отклонении 20 руб., а у женщин – 2780 руб. при среднем квадратическом отклонении 30 руб. Определите, можно ли считать расхождение между заработной платой мужчин и женщин случайным.
Решение
А. Находим абсолютную разность средних:
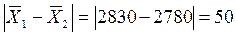руб.
Б. Средняя ошибка разности
.
В. Находим t:
.
Поскольку в данной задаче в каждой выборке n > 20, t расч сравниваем с 3. Так как t расч>3, то расхождение между средней заработной платой мужчин и женщин нельзя считать случайным.
4.2. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задача 4.1
При проверке веса импортируемого груза на таможне методом случайной повторной выборки было отобрано 200 изделий. В результате был установлен средний вес изделия, равный 30 г, при среднем квадратическом отклонении 4 г. С вероятностью 0,997 определите интервалы, в которых находится средний вес изделия в генеральной совокупности.
Задача 4.2
В городе проживает 250 тыс. семей. Для определения среднего числа детей в семье была организована 2%-ная случайная бесповторная выборка семей. По ее результатам получено следующее распределение семей по количеству детей (табл. 4.2).
Таблица 4.2
| Число детей в семье | ||||||
| Количество семей |
С вероятностью 0,954 найдите пределы, в которых будет находиться среднее число детей в генеральной совокупности.
|
|
|
Задача 4.3
Средняя продолжительность горения, установленная путем испытания 10 случайно отобранных электрических лампочек, оказалась равной 1280 ч при среднем квадратическом отклонении 18 ч.
С какой вероятностью можно утверждать, что допущенная при этом предельная ошибка выборки (т.е. расхождение между выборочной и генеральной средней) не превысит 12 ч?
Задача 4.4
На городской телефонной станции в порядке собственно случайной выборки проведено 100 наблюдений и установлено, что средняя продолжительность одного телефонного разговора составляет 10 мин при среднем квадратическом отклонении 5 мин.
1. С вероятностью 0,997 определите доверительные пределы для генеральной средней.
2. Можно ли считать данную выборку репрезентативной?
3. С какой вероятностью можно утверждать, что при определении средней продолжительности одного телефонного разговора допущена ошибка, не превышающая 1 мин?
Задача 4.5
На основе выборочного обследования 600 рабочих (n = 600) одной из отраслей промышленности установлено, что удельный вес численности женщин составил 0,4 (w = 0,4).
С какой вероятностью можно утверждать, что при определении доли женщин, занятых в этой отрасли, допущена ошибка (D), не превышающая 5% (0,05)?
Задача 4.6
Из партии готовой продукции в порядке механической выборки проверено 50 лампочек на продолжительность горения. Последняя оказалась равна 840 ч при среднем квадратическом отклонении 60 ч.
Определите:
1) среднюю ошибку (µ) выборочной средней продолжительности горения лампочки;
2) доверительные пределы продолжительности горения лампочки в генеральной совокупности с вероятностью 0,95.
Задача 4.7
Из партии готовой продукции в порядке механической бесповторной выборки проверено 400 изделий и установлено, что 80% из них соответствует первому сорту.
С вероятностью 0,9545 определите долю (процент) продукции первого сорта во всей партии.
|
|
|
Задачу решите в двух вариантах:
1) численность изделий в партии готовой продукции неизвестна;
2) в партии готовой продукции 2000 изделий.
Задача 4.8
В порядке случайной выборки обследован дневной надой молока 50 коров. Результаты обследования приведены в табл. 4.3.
Определите:
1) по выборочным данным средний надой молока от одной коровы;
2) среднюю ошибку выборки;
3) вероятность того, что при определении выборочного среднего надоя молока допущена ошибка, не превышающая 1 кг.
Таблица 4.3
| Дневная удойность, кг | Количество коров |
| 10-14 | |
| 14-18 | |
| 18-22 | |
| Свыше 22 | |
| Итого |
Задача 4.9
При случайном способе отбора из партии было взято 100 проб продукта А. В результате исследования установлено, что влажность продукта А в выборке составляет 9% при среднем квадратическом отклонении 1,5%. С вероятностью 0,954 определите пределы, в которых находится средняя влажность продукта А в партии.
Задача 4.10
Для изучения общественного мнения населения области о проведении определенных мероприятий методом случайного отбора было опрошено 600 человек. Из числа опрошенных 360 человек одобрили мероприятия.
С вероятностью 0,997 определите пределы, в которых находится доля лиц, одобривших мероприятия.
Задача 4.11
Для определения среднего возраста рабочих предприятия была произведена выборка рабочих методом случайного бесповторного отбора. В результате обследования получены следующие данные (табл. 4.4).
Таблица 4.4
| Возраст рабочих, лет | 20-30 | 30-40 | 40-50 | 50-60 |
| Число рабочих, чел. |
С вероятностью 0,997 определите:
1) пределы, в которых находится средний возраст рабочих предприятия;
2) пределы, в которых находится доля рабочих предприятия в возрасте старше 50 лет.
Задача 4.12
Из партии готовой продукции методом случайного отбора отобрано 250 изделий, из которых пять оказались бракованными. Определите с вероятностью 0,954 возможные пределы процента брака во всей партии. Объем выборки составляет 10% всего объема готовой продукции.
Задача 4.13
В выборах мэра примут участие около 1 млн избирателей. Кандидат М будет выбран, если за него проголосуют более 50% избирателей. Накануне выборов проведен опрос случайно отобранных 1000 избирателей: 540 из них сказали, что будут голосовать за М. Укажите, можно ли при уровне доверительной вероятности 0,954 утверждать, что М победит на выборах.
|
|
|
Задача 4.14
На одном из рынков города дважды за день проведено выборочное обследование цен на картофель. При первом обследовании было опрошено 10 продавцов, при втором – 15. Средняя цена картофеля в первой выборке оказалась равной 5 руб. при среднем квадратическом отклонении 0,6 руб., а во второй выборке – соответственно 5,5 и 0,8 руб. (т.е. n 1 = 10 чел., x 1 = 5 руб., σ1 = 0,6 руб. и n 2 = 15 чел., x 2 = 5,5 руб., σ2 = 0,8 руб.).
Определите, случайны или нет расхождения между x 1 и x 2.
Задача 4.15
Исследуемая партия состоит из 5 тыс. деталей. Предполагается, что партия деталей содержит 8% бракованных. Определите необходимый объем выборки, чтобы с вероятностью 0,997 установить долю брака с погрешностью не более 2%.
Задача 4.16
В городе А проживает 10 000 семей. С помощью механической выборки предполагается определите долю семей с тремя детьми и более. Какова должна быть численность выборки, чтобы с вероятностью 0,954 ошибка выборки не превышала 0,02, если на основе предыдущих обследований известно, что дисперсия равна 0,2?
Задача 4.17
В районе проживает 1000 семей. Предполагается провести их выборочное обследование методом случайного бесповторного отбора для нахождения среднего размера семьи. Определите необходимую численность выборки при условии, что с вероятностью 0,997 ошибка выборки не превысит одного человека при среднем квадратическом отклонении в три человека.
Задача 4.18
Сколько рабочих завода нужно обследовать в порядке случайной выборки для определения средней заработной платы, чтобы с вероятностью Р, равной 0,954, можно было гарантировать ошибку не более 50 руб.? Предполагаемое среднее квадратическое отклонение заработной платы σ = 200 руб.
Задача 4.19
Намечается выборочное обследование покупателей в одном из крупных универмагов города в целях определения доли покупателей из других городов. Каким должен быть объем выборки, чтобы с вероятностью 0,9545 можно было гарантировать точность результата до 5%? На основе предыдущих исследований дисперсию доли можно принять равной 0,4 при среднем потоке покупателей 5000 чел.
|
|
|
Задача 4.20
В 100 туристических агентствах города предполагается провести обследование среднемесячного количества реализованных путевок методом механического отбора. Какова должна быть численность выборки, чтобы с вероятностью 0,683 ошибка не превышала 3 путевок, если по данным пробного обследования дисперсия составляет 225?
Задача 4.21
С целью определения доли сотрудников коммерческих банков области в возрасте старше 40 лет предполагается организовать типическую выборку пропорционально численности сотрудников мужского и женского пола с механическим отбором внутри групп. Общее число сотрудников банков составляет 12 тыс. человек, в том числе 7 тыс. мужчин и 5 тыс. женщин.
На основе предыдущих обследований известно, что средняя из внутригрупповых дисперсий составляет 1600. Определите необходимый объем выборки при вероятности 0,997 и ошибке 5%.
Задача 4.22
В акционерном обществе 200 бригад. Планируется проведение выборочного обследования с целью определения удельного веса рабочих, имеющих профессиональные заболевания. Известно, что межсерийная дисперсия доли равна 225. С вероятностью 0,954 рассчитайте необходимое количество бригад для обслуживания рабочих, если ошибка выборки не должна превышать 5%.
Раздел 5. Статистические показатели динамики
5.1. МЕТОДИЧЕСКИЕ УКАЗАНИЯ
И РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
Числовые значения того или иного статистического показателя, составляющие ряд динамики, называют уровнями ряда и обозначают через y.
При анализе рядов динамики необходимо проследить за направлением и размером изменений уровней во времени. С этой целью рассчитывают следующие показатели.
1. Абсолютные приросты уровней (разность между двумя уровнями):
цепные Dуц = уi – уi-1; (5.1)
и базисные Dуб = уi –у0. (5.2)
2. Темпы роста (изменения) ТР – относительные показатели, рассчитываемые как отношение двух уровней ряда. Темпы роста могут быть цепными, если каждый уровень ряда сопоставляется с предыдущим:
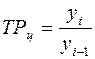, (5.3)
и базисными, когда каждый уровень ряда сопоставляется с уровнем одного какого-то периода (часто это начальный – базисный – уровень ряда):
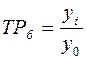. (5.4)
Темпы роста как относительные величины могут выражаться в виде коэффициентов, т.е. простого кратного отношения (база сравнения принимается за единицу), и в процентах (база сравнения принимается за 100 единиц).
3. Темпы прироста (снижения) уровней ТПр – относительные показатели, показывающие, на сколько процентов данный уровень (y) больше (или меньше) другого, принимаемого за базу сравнения.
|
|
|
Темп прироста можно рассчитать двумя способами:
1) путем вычитания 100% из темпа роста:
ТПр =ТР -100%;(5.5)
2) как процентное отношение абсолютного прироста к тому уровню, по сравнению с которым рассчитан абсолютный прирост:
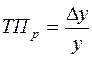. (5.6)
Методы расчета среднего уровня ряда динамики зависят от его вида и способов получения статистических данных.
В интервальном ряду с равностоящими во времени уровнями расчет производится по формуле средней арифметической простой
, (5.7)
где п – число уровней ряда.
Для интервального ряда с разными временными интервалами средний уровень вычисляется по формуле средней взвешенной
, (5.8)
где ti – время, в течение которого уровень y считается неизменным.
Для моментного ряда, содержащего n уровней с равными промежутками между датами (моментами), средний уровень определяется по формуле
. (5.9)
Эта средняя известна в статистике как средняя хронологическая простая.
Для неравностоящих уровней моментного ряда средняя рассчитывается по формуле средней хронологической взвешеннной:
. (5.10)
Средний абсолютный прирост определяется как
(5.11)
или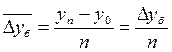 
, (5.12)
где п – число периодов.
Средний темп роста рассчитывается из выражений
, (5.13)
где п – число темпов роста, а П – знак произведения,
или 
. (5.14)
Средний темп прироста вычисляется по формуле
. (5.15)
Абсолютное значение одного процента прироста (А1%) определяется из выражения
(5.16)
или | А1%| может быть исчислен как одна сотая часть предыдущего уровня.
Среднее абсолютное значение одного процента прироста за несколько (п) лет рассчитывается по формуле
. (5.17)
Пример 5.1
Пусть имеются следующие данные о производстве зерна в одном из хозяйств за 5 лет (табл. 5.1).
Таблица 5.1
| Год | |||||
| Производство зерна, тыс. ц. уi |
Рассчитайте:
1) средний уровень за 5 лет;
2) ежегодные абсолютные приросты;
3) ежегодные темпы роста;
4) среднегодовой темп роста за 4 года – с 2003 по 2006 г.;
5) темп прироста (цепной) за 2006 г.;
6) абсолютное значение одного процента прироста для 2006 г.
Решение
1. Так как это интервальный ряд, то средний уровень ряда (среднегодовое производство зерна) определим как среднюю арифметическую простую:
тыс. ц.
2. Ежегодные абсолютные приросты находим как цепную разность между двумя уровнями:
для 2003 г. Δ у1 = 54 – 50 = 4 тыс. ц;
для 2004 г. Δ у2 = 62 – 54 = 8 тыс. ц;
для 2005 г. Δ у3 = 70 – 62 = 8 тыс. ц;
для 2006 г. Δ у4 = 80 – 70 = 10 тыс. ц.
3. Ежегодные темпы роста (цепные) находим как отношение уровня каждого года к предыдущему:
для 2003 г. ТР1 = 54 / 50 = 1,08 = 108%;
для 2004 г. ТР2 = 62 / 54 = 1,148 = 114,8%;
для 2005 г. ТР3 = 70 / 62 = 1,129 = 112,9%;
для 2006 г. ТР4 = 80 / 70 = 1,143 = 114,3%.
4. Среднегодовой темп роста можно рассчитать по формуле (5.13) как среднюю геометрическую из годовых темпов роста
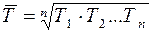
либо по формуле (5.14)
.
По первой формуле
.
По второй формуле
,
т.е. среднегодовой темп роста за 4 года (с 2003 по 2006 г.) равен 112,5%.
5. Темп прироста определяем по формуле (5.5):
ТПр = 114,3%-100%=14,3%.
6.Абсолютное значение одного процента прироста для 2006 г. определяется как одна сотая предыдущего уровня:
А1%=70 тыс. ц / 100=0,7 тыс. ц.=700 ц
или по формуле (5.16):
А1%=10 тыс. ц / 14,3%=700 ц.
Пример 5.2
Определите время, в течение которого ряд с бόльшим средним показателем динамики, но меньшим начальным уровнем, догонит другой ряд с меньшим средним показателем динамики, но с бόльшим начальным уровнем.
Преобразуем формулу (5.14), обозначив 
через 
:
.
Тогда 
.
Необходимо определить, когда 
.
Решение
.
Прологарифмируем:
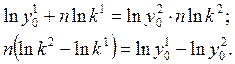
Отсюда
.
Есл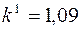и 
, 
и 
, 
,
то 
.
Следовательно, через 11 лет уровень второго ряда сравняется с уровнем первого ряда.
Пример 5.3
Имеются данные о производстве продукции за 2003-2005 гг., млн руб. (табл. 5.2).
Таблица 5.2
| Годы | 2003 г. | 2004 г. | 2005 г. |
| Произведено продукции |
Определите среднегодовое производство продукции.
Решение
Среднегодовое производство продукции за 2003-2005 гг. будет определяться по формуле (5.7):
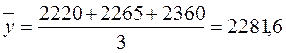млн руб.
Пример 5.4
Имеются следующие данные об остатках сырья и материалов на складе предприятия, млн руб.:
на 1/I – 400; на 1/II – 455; на 1/IV – 460.
Определите среднемесячный остаток сырья и материалов на складе предприятия за I квартал.
Решение
По условию задачи имеем моментный ряд динамики с равными интервалами, поэтому средний уровень ряда будет исчислен по формуле средней хронологической простой (5.9):
млн руб.
Пример 5.5
Имеются следующие данные о товарных запасах розничного торгового предприятия за 2004 г. (табл. 5.3).
Таблица 5.3
| 1 января | 1 мая | 1 августа | 1 января 2005 г. |
| 61,1 | 57,5 | 51,3 | 74,7 |
Определите средний уровень товарных запасов.
Решение
Число месяцев между приведенными датами 4, 3, 5.
Средний уровень товарных запасов за год для моментного ряда динамики с неравными интервалами вычислим по формуле средней хронологической взвешенной (5.10):
.
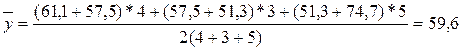Важным направлением в исследовании закономерностей динамики социально-экономических процессов является изучение общей тенденции развития (тренда).
Наиболее распространенными методами выделения тренда являются метод скользящей средней и аналитический метод.
Метод скользящей средней заключается в том, что вычисляется средняя величина из определенного количества уровней (например, четырех) с отбрасыванием при вычислении каждой новой скользящей средней одного уровня слева и присоединением одного уровня справа:
; 
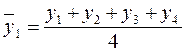и т.д.
Скользящая средняя дает более или менее плавное изменение уровней ряда.
Пример 5.6
Имеются данные о потреблении овощей по области в 1997-2005 гг. на одного человека в месяц, кг (у) (табл. 5.4).
Таблица 5.4
| 1997 г. | 1998 г. | 1999 г. | 2000 г. | 2001 г. | 2002 г. | 2003 г. | 2004 г. | 2005 г. |
| 10,0 | 10,7 | 12,0 | 10,3 | 12,9 | 16,3 | 15,6 | 17,8 |
Выявим основную тенденцию потребления овощей методом скользящей средней. Рассчитаем трехлетние скользящие средние:
кг;
и т.д.
Получим ряд (табл. 5.5).
Таблица 5.5
| 1998 г. | 1999 г. | 2000 г. | 2001 г. | 2002 г. | 2003 г. | 2004 г. |
| 10,9 | 11,0 | 11,8 | 13,2 | 15,9 | 16,6 | 17,1 |
Таким образом, выявилась явная тенденция к росту потребления овощей.
Получить обобщенную статистическую оценку тенденции развития явления (тренда) можно методом аналитического выравнивания. В этом случае ряд динамики выражается математической зависимостью уровней ряда y от времени t:
y=f (t).
Рекомендуется при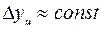 
(равномерное развитие) использовать модели типа
. (5.18)
При равноускоренном (равнозамедленном) развитии с постоянными темпами прироста 
используется парабола второго порядка
. (5.19)
Для развития с переменным ускорением (замедлением) используется парабола третьего порядка
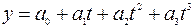. (5.20)
При стабильных темпах роста 
развитие идет по экспоненте и отображается показательной функцией
. (5.21)
Для определения параметров математических моделей применяется способ отсчета времени от условного начала, при этом 
.
При этом для прямолинейной функции:
; (5.22)
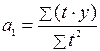; (5.23)
для показательной функции:
;
; (5.24)
; (5.25)
для параболы второго порядка:
;
; (5.26)
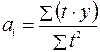; (5.27)
. (5.28)
В случае, если основные признаки (характер динамики развития) типовых моделей не выражаются явно, необходимо просчитать несколько моделей и выбрать из них адекватную. Адекватность определяется по значению стандартизированной ошибки аппроксимации
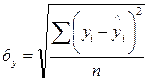, (5.29)
где 
– значение уровня i- того года (данные в задании),
, – значение уровня i- того года, полученное по математической модели.
Суммирование производится по заданным исходным данным по n годам. Адекватной считается та модель, для которой 
минимальна.
Подробнее расчеты по построению математических моделей тренда рассмотрены в [17].
5.2. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задача 5.1
О производстве картофеля в хозяйствах населения РФ за 2001-2006 гг. имеются следующие данные (5.6).
Таблица 5.6
| Год | ||||||
| Производство картофеля, млн т | 24,8 | 29,9 | 31,1 | 29,8 | 35,9 | 34,9 |
Определите:
1) абсолютные приросты производства картофеля по годам (цепные);
2) цепные и базисные коэффициенты роста;
3) среднегодовой уровень производства картофеля за 2001-2006 гг.;
4) среднегодовой коэффициент роста производства картофеля в хозяйствах населения за 2002-2006 гг.
Задача 5.2
Об остатках наличных денег у населения РФ в первой половине 2004 г. имеются следующие данные (табл. 5.7).
Таблица 5.7
| Месяц | Январь | Февраль | Март | Апрель | Май | Июнь | Июль |
| Остаток денег на начало месяца, трлн руб. | 75,8 | 70,5 | 74,5 | 77,1 | 84,7 | 88,4 | 100,5 |
Рассчитайте:
1) средний остаток наличных денег у населения за январь-июнь;
2) среднемесячный темп роста наличных денег у населения за 6 месяцев 2004 г.
Задача 5.3
О мировых ценах на кофе в Бразилии имеются следующие данные (за 1 кг) (табл. 5.8).
Таблица 5.8
| Год | |||||||
| Цена, $ | 1,3 | 1,27 | 0,95 | 1,1 | 2,55 | 2,73 | 2,21 |
|
|
|
