Для нашего примера эмпирическое корреляционное отношение 8 глава

Пример 7.3

Оцените наличие связи между работниками торговли, распределенными по полу и содержанию работы. Результаты исследования сведены в статистическую таблицу (табл. 7.5).

Таблица 7.5

Распределение работников торговли по полу
и оценке содержания работы

Работа	Мужчины	Женщины	Всего
Интересная	300 (а)	201 (b)	501 (a+b)
Неинтересная	130 (c)	252 (d)	381 (c+d)
Итого	430 (a+c)	453 (b+d)	883 (a+b+c+d)

 

В приведенном примере величина К _а будет равна 0,486.

Величина коэффициента в нашем примере соответствует среднему размеру связи, несмотря на различие мнений о своей работе мужчин и женщин.

Пример 7.4

Исследовалась социально-демографическая характеристика случайных потребителей наркотиков в зависимости от их семейного положения в одном из регионов РФ (тыс. чел.). Результаты обследования характеризуются следующими данными (табл. 7.6).

Таблица 7.6

Группы потребителей наркотиков	Семейное положение	Всего
замужем (женат)	не замужем (не женат)
Потреблял Не потреблял	10,0 2,5	14,5 4,5	24,5 7,0
Итого	12,5	19,0	31,5

Рассчитайте коэффициент ассоциации и контингенции.

 

Решение

.

 

Вывод. Так как К_а < 0,5 и К_к < 0,3, то потребление наркотиков случайными потребителями не зависит от их семейного положения.

Для определения тесноты связи как между количественными, так и между качественными признаками при условии, что значения этих признаков могут быть упорядочены или проранжированы по степени убывания или возрастания признака, может быть использован коэффициент Спирмена (коэффициент ранговой корреляции) Р, который рассчитывается по следующей формуле:

, (7.13)

где – квадраты разности рангов связанных величин х и у,

;

N – число наблюдений (число пар рангов).

Ранг – это порядковый номер значений признака, расположенных в порядке возрастания или убывания их величин.

Пример 7.5

Рассмотрим наличие связи между обеспеченностью товарной продукцией ряда предприятий и накладными расходами по реализации (табл. 7.7).

Таблица 7.7

Обеспеченность товарной продукцией, млн руб. х	Накладные расходы по реализации, тыс. руб. у	Ранжирование	Сравнение рангов	Разность рангов
x	ранг	y	ранг
12,0 18,8 11,0 29,0 17,5 23,4 35,6 15,4 26,1 20,7		11,0 12,0 15,4 17,5 18,8 20,7 23,4 26,1 29,0 35,0						-1 -1 -1 -1 -5
Итого

 

По данным табл. 7.7 получим следующие значения коэффициента Спирмена:

Пользуясь определением тесноты связи по шкале Чеддока, можно сказать, что полученная связь заметная.

Для определения тесноты связи между произвольным числом ранжированных признаков применяется множественный коэффициент ранговой корреляции W (или коэффициент конкордации), который вычисляется по формуле

(7.14)

где m – количество факторов;

n – число наблюдений;

S – отклонение суммы квадратов рангов от средней квадратов рангов.

Пример 7.6

Определите тесноту связи между уставным капиталом, числом выставленных акций и числом занятых на предприятиях, выставивших акции на чековые аукционы в 2004 г. (табл. 7.8).

Таблица 7.8

Расчет коэффициента конкордации (данные условия)

N предприятия	Уставный капитал, усл. ед. Х	Число выставленных акций У	Число занятых на предприятии Z				Сумма рангов	Квадраты сумм
	2 954 1 605 4 102 2 350 2 625 1 795 2 813 1 751 1 700 2 264
-	-	-	-	-	-	-		2 863

 

Коэффициент конкордации говорит о том, что связь между заданными параметрами слабая.

Среди непараметрических методов оценки тесноты связи определенный интерес представляет коэффициент Фехнера. Он определяется на основе соотношения знаков отклонений значений исследуемых признаков x и y от их средних значений.

Коэффициент Фехнера рассчитывается по формуле

, (7.15)

где а – число совпадений отклонений и по знаку;

b – число несовпадений отклонений и по знаку;

(а+ b) – общее количество значений признака.

Чем ближе величина коэффициента Фехнера к единице, тем теснее связь между изучаемыми признаками.

Пример 7.7

У восьми учащихся школы зафиксировано следующее количество баллов, полученных за самостоятельные работы: по математике – X и гуманитарным дисциплинам – Y (табл. 7.9).

Определите, существует ли между ними корреляция, через коэффициент Фехнера.

Таблица 7.9

Ст-т	X		Y		а	b
А		+		+
Б		-		+
В		-		-
Г		-		-
Д		+		-
Е		+		-
Ж		-		-
З		+		+
Среднее	70,1		59,8

 

.

Когда каждый из качественных признаков состоит более чем из двух групп, то для определения тесноты связи возможно применение коэффициентов взаимной сопряженности Пирсона и Чупрова, которые вычисляются по формулам

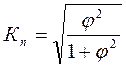; (7.16)

, (7.17)

где – показатель взаимной сопряженности, определяется по формуле

(7.18)

К ₁ – число значений (групп) первого признака;

К ₂ – число значений (групп) второго признака.

Чем ближе К _п и К _ч к 1, тем связь теснее.

Пример 7.8

Исследовалась зависимость между оценкой уровня жизни респондентов Москвы и типом предприятия, на котором они работают. Данные, характеризующие опрос, приведены в табл. 7.10. Необходимо определить коэффициенты взаимной сопряженности Пирсона и Чупрова.

Таблица 7.10

Тип предприятия	Оценка уровня жизни респондентов	Итого
Вполне удовлетворен	Скорее удовлетворен	Скорее не удовлетворен	Совсем не удовлетворен
Государственное
Акционерное общество
Арендованное
Частное
Итого

 

Решение

По формуле (7.18)

;

;

= .

Вывод. Оценка уровня жизни респондентов не зависит от типа предприятия, на котором они работают.

В статистике существуют модификация коэффициента Пирсона, например через расчет -критерия. Коэффициент сопряженности (К_п) вычисляется по формуле

, (7.19)

где . (7.20)

7.2. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

Задача 7.1

Имеются данные по группе однородных предприятий (табл. 7.11).

Таблица 7.11

№ предприятия
Основные фонды (ден. ед.)
Продукция (ден. ед.)	9,9	10,8	11,5	12,0	12,4

 

1. Постройте управление линейной корреляционной зависимости продукции от основных фондов.

2. Вычислите коэффициент эластичности.

3. Вычислите линейный коэффициент корреляции.

4. Сделайте выводы.

Задача 7.2

По пяти однородным предприятиям имеются следующие данные (табл. 7.12).

Таблица 7.12

№ предприятия
Количество рабочих с профессиональной подготовкой, %
Количество бракованной продукции, %

 

Постройте однофакторную линейную модель зависимости между выпуском бракованной продукции и профессиональной подготовкой рабочих.

Вычислите коэффициент эластичности и показатель тесноты корреляционной связи.

Задача 7.3

О росте 8 пар братьев и сестер имеются следующие данные (табл. 7.13).

Таблица 7.13

Рост брата, см	Рост сестры, см

 

Определите тесноту зависимости между ростом братьев и сестер на основе коэффициента Фехнера.

Задача 7.4

По 8 сахарным заводам о стоимости основных производственных фондов, х (млн руб.) и суточной переработке сахарной свеклы, у (тыс. т.) имеются следующие данные (табл. 7.14).

Таблица 7.14

х	у
2,0	8,9
2,3	10,0
2,4	9,9
2,9	10,3
2,9	10,0
3,7	13,0
3,7	12,8
4,1	13,1

 

1. Найдите уравнение регрессии у и х и определите значимость его параметров (с помощью t -критерия).

2. Измерьте тесноту зависимости между х и у с помощью:

а) корреляционного отношения;

б) линейного коэффициента корреляции.

Задача 7.5

Имеются данные по 10 хозяйствам о количестве внесенных минеральных удобрений под зерновыми, х (кг/га) и об урожайности зерновых, у (ц/га) (табл. 7.15).

Таблица 7.15

х	у
	13,5
	14,0
	14,0
	14,3
	14,0
	15,0
	18,2
	15,0
	17,0
	20,0

 

Измерьте тесноту связи между х и у с помощью линейного коэффициента корреляции.

Задача 7.6

Совокупность разбита по определенному признаку x на 3 группы, численность которых: n ₁ = 10, n ₂ = 20, n ₃ = 20.

Групповые средние исследуемого показателя Х равны следующим величинам: х ₁ =5, х ₂ = 8, х ₃ = 15.

Определите величину эмпирического корреляционного отношения, если общая дисперсия показателя Х равна 18,5.

Задача 7.7

Были опрошены 400 работников коммерческих структур и 400 работников бюджетных организаций, которых просили ответить на вопрос, довольны ли они своей заработной платой. Их ответы распределились следующим образом (табл. 7.16).

Таблица 7.16

Работающие	Довольные Заработной платой	Недовольные Заработной платой	Итого
В коммерческих структурах
В бюджетных организациях
Итого работников

 

1. С помощью критерия Пирсона определите, случайно или не случайно данное распределение.

2. Рассчитайте коэффициенты ассоциации и контингенции.

Задача 7.8

О распределении 200 молочных ферм области по производительности труда и себестоимости молока имеются следующие данные (табл. 7.17).

Таблица 7.17

Себестоимость	Производительность
Высокая	Средняя	Низкая	Итого
Высокая
Средняя
Низкая
Итого

 

1. С помощью критерия Пирсона проверьте, случайно ли данное распределение, т.е. существует ли зависимость между производительностью труда и себестоимостью молока.

2. Измерьте тесноту зависимости между указанными показателями с помощью коэффициентов взаимной сопряженности Пирсона и Чупрова.

Задача 7.9

По Северо-Западному району РФ за 2004 г. имеются следующие данные (табл. 7.18).

Таблица 7.18

Область	Урожайность зерновых, ц/га	Надой молока на одну корову, кг	Урожайность картофеля, ц/га
Ленинградская	16,3
Новгородская	10,4
Псковская	10,6
Вологодская	10,8

 

С помощью коэффициента конкордации определите, согласуется ли «рейтинг» областей по всем показателям.

Задача 7.10

О распределении 20 заводов по объему выпуска и о прибыли отдельных предприятий имеются следующие условные данные (табл. 7.19).

Таблица 7.19

Объем выпуска, тыс. ед.	Число заводов	Прибыль по отдельным заводам, млн руб.
До 10		1,2,3
11-20		2,3,4,5,6
21-30		4,5,6,7,7,8,8
31-40		7,9,11
41-50		12,13

 

С помощью эмпирического корреляционного отношения измерьте тесноту зависимости прибыли от объема выпуска.

Задача 7.11

Оценка студентами профессиональных качеств преподавателей по дисциплине «Статистика» представлена в табл. 7.20.

Таблица 7.20

Оценка Кри- терии оценки преподавателей	Высокая	Средняя	Низкая	Затруднялись ответить	Итого
Знание предмета
Умение обучать
Восприимчивость к новому
Способность к саморазвитию
Итого

 

Рассчитайте коэффициент Пирсона и сделайте выводы.

Задача 7.12

Получены следующие результаты анкетного обследования рабочих, имеющих вторичную занятость (табл. 7.21).

Таблица 7.21

Дополнительно заняты	Количество ответов
Мужчин	Женщин	Всего
На одной работе
На двух работах
На трех работах		-
Всего

 

Измерьте тесноту зависимости между признаками, положенными в основу группировки, с помощью коэффициентов взаимной сопряженности:

а) Пирсона; б) Чупрова.

Задача 7.13

По восьми предприятиям об энерговооруженности труда (х) и производительности труда (у) имеются следующие условные данные (табл. 7.22).

Таблица 7.22

Потребление электроэнергии на одного рабочего, кВт-ч, х	Выработка на одного рабочего, тыс. руб., у
	2,3
	3,8
	4,0
	3,9
	4,5
	5,4
	5,1
	6,0

 

Измерьте тесноту зависимости между х и у, используя:

1) коэффициент Фехнера;

2) линейный коэффициент корреляции.

Задача 7.14

О стаже работы (х) 10 рабочих одной специальности и выработке ими продукции за смену (у) имеются следующие данные (табл. 7.23).

Таблица 7.23

Номер рабочего	Производственный стаж, лет, х	Выработка продукции за смену, шт., у

 

Измерьте тесноту зависимости между х и у с помощью коэффициентов Фехнера и линейного коэффициента корреляции.

Задача 7.15

О проблеме совмещения учебы с работой были опрошены 100 студентов дневного отделения. Имеются следующие результаты опроса (табл. 7.24).

Таблица 7.24

Студенты	Численность студентов в возрасте	Итого
До 20 лет	Старше 20 лет
Неработающие
Сочетающие работу с учебой
Итого

 

Рассчитайте коэффициенты ассоциации и контингенции и сделайте выводы о тесноте зависимости между признаками, положенными в основу группировки.

ТЕСТОВЫЕ ЗАДАНИЯ
ДЛЯ ПРОВЕРКИ ЗНАНИЙ СТУДЕНТОВ

1. Статистическое наблюдение и группировка

1. Группировка, в которой изучается структура совокупности, называется:

а) структурной

б) типологической

в) аналитической

г) многомерной

2. Группировочный признак может быть:

а) и количественным, и качественным

б) количественным

в) качественным

г) корреляционным

3. Величина интервала определяется:

а) разностью верхней и нижней границ интервала

б) верхней границей интервала

в) нижней границей интервала

г) полусуммой нижней и верхней границ интервала

4. Вторичная группировка осуществляется методом:

а) укрупнения интервалов и долевой перегруппировки

б) уменьшения интервалов

в) и уменьшения, и укрупнения интервалов

г) долевой перегруппировки

5. Сводка статистических данных по форме организации обработки данных может быть:

а) централизованной и децентрализованной

б) сплошной

в) простой

г) выборочной

6. Статистические таблицы используются для:

а) компактного наглядного представления и анализа статистиче-
ских данных

б) изложения результатов наблюдения

в) подсчёта итогов

г) записей

7. Назовите основные элементы статистической таблицы:

а) подлежащее и сказуемое

б) графы и строки

в) заглавие

г) цифры

д) названия граф и строк

8. Подлежащее таблицы – это:

а) объект статистического наблюдения

б) совокупность явлений

в) перечень единиц

г) любые показатели

д) цифровые данные

9. Сказуемое статистической таблицы – это:

а) показатели, характеризующие изучаемый объект

б) характеристики единиц

в) цифры

г) значения строк

д) цифры в графах

10. Макет статистической таблицы – это:

а) таблица без цифр, имеющая общий заголовок, заглавия граф
и строк

б) план разработки материалов

в) программа наблюдения

г) сводка статистических данных

11. Вид статистической таблицы определяется:

а) по подлежащему таблицы

б) по сказуемому таблицы

в) по подлежащему и сказуемому таблицы

г) по графам

д) по строкам

12. Укажите отличительную черту простых таблиц:

а) не имеют в подлежащем группировки, а содержат перечень
либо единиц совокупности, либо единиц времени, либо
территорий

б) имеют группировку в подлежащем по одному признаку

в) имеют группировку в сказуемом по одному признаку

г) имеют группировку в подлежащем по двум признакам

д) содержат в сказуемом несколько группировок

13. Группировка, в которой происходит разбиение однородной совокупности на группы, называется:

а) типологической

б) структурной

в) аналитической

г) многомерной

14. По видам группировочных признаков выделяют:

а) качественный признак

б) количественный признак

в) факторный признак

г) результативный признак

15. Наименьшее значение признака в интервале называется:

а) кумулятивной частотой

б) нижней границей интервала

в) верхней границей интервала

г) шагом интервала

16. Статистическая таблица представляет собой:

а) инструкцию по заполнению форм отчетности

б) форму наиболее рационального изложения результатов статистического наблюдения

в) сведения, расположенные по строкам и графам

г) план проведения наблюдения

17. Подлежащие в статистической таблице расположено:

а) слева на строках

б) справа в колонках, графах, столбцах

в) в заглавии статистической таблицы

г) в итоговых строках и графах

18. Группировка, построенная по двум признакам, называется:

а) рядом распределения

б) простой группировкой

в) комбинационной группировкой

г) статистической таблицей

19. Сводка статистических материалов включает следующие этапы:

а) контроль первичных (фактических) данных

б) группировку

в) подсчет итогов

г) план

20. При разбиении однородной совокупности на группы получается... группировка:

2. Статистическая совокупность и ее характеристика

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: