Для нашего примера эмпирическое корреляционное отношение 6 глава

1. Рассчитайте основные аналитические показатели ряда динамики (абсолютные приросты, темпы роста и др.).

2. Определите уравнение тренда мировых цен на кофе.

Задача 5.4

Производство шерсти в фермерских хозяйствах РФ характеризуется следующими данными (табл. 5.9).

Таблица 5.9

Год
Произведено тыс. т	1,4	2,9	3,3	4,2	3,6

 

1. Определите среднегодовой темп роста производства шерсти за 2000-2005 гг.

2. Проведите аналитическое выравнивание уровней ряда и на основе уравнения тренда спрогнозируйте производство шерсти в 2007 г.

Задача 5.5

О динамике валового внутреннего продукта (ВВП) РФ имеются следующие данные (в сопоставимых ценах) (табл. 5.10).

Таблица 5.10

Год
ВВП, % к предыдущему году		85,5	91,3	87,3	95,9	96,6	100,9	95,4

 

1.Определите процент изменения ВВП в 2005 г. по сравнению с 1997 г.

2. Рассчитайте среднегодовой темп изменения ВВП за 1998-2005 гг.

Раздел 6. Экономические индексы

6.1. МЕТОДИЧЕСКИЕ УКАЗАНИЯ
И РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ

6.1.1. ОБЩАЯ ТЕОРИЯ ИНДЕКСОВ

Индекс в статистике – это обобщающий показатель сравнения двух совокупностей, состоящих из элементов, непосредственно не поддающихся суммированию.

Переход от натурально-вещественной формы выражения товарных масс к стоимостной является основой индексного метода. Именно денежное выражение стоимости отдельных товаров устраняет их несуммарность.

Индивидуальные индексы характеризуют изменения отдельных единиц статистической совокупности.

Общие индексы выражают сводные (обобщающие) результаты совместного изменения всех единиц, образующих статистическую совокупность.

Индивидуальные индексы принято обозначать i, а общие – I.

Основным элементом индексного отношения является индексируемая величина. Под индексируемой величиной понимается значение признака статистической совокупности, изменение которой является объектом изучения. Так, при изучении изменения цен индексируемой величиной является цена единицы товара р. При изучении изменения физического объема товарной массы в качестве индексируемой величины выступают данные о количестве товаров в натуральных измерителях q.

Индивидуальный индекс физического объема реализации товаров i_q определяется по формуле

(6.1)

где q₁ и q₀ – количество производства или продажи отдельной товарной разновидности в текущем и базисном периодах соответственно. Индекс показывает, во сколько раз возрос (уменьшился) выпуск какого-либо одного товара в отчетном периоде по сравнению с базисным.

Для определения индивидуальных индексов цен i_p применяется формула

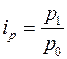, (6.2)

где p₁ и p₀ – цены за единицу товара в текущем и базисном периодах.

Общие индексы характеризуют изменения совокупности в целом и могут исчисляться как по агрегатной, так и по средней форме (среднего арифметического или среднего гармонического индекса). Выбор формы общих индексов зависит от характера исходных данных.

6.1.2. АГРЕГАТНЫЕ ИНДЕКСЫ

Агрегатный индекс – основная форма экономического индекса.

Индекс стоимости продукции, или товарооборота (I_pq), представляет собой отношение стоимости продукции в текущем периоде (Σp₁q₁) к стоимости продукции в базисном периоде (Σp₀q₀) и определяется по формуле

. (6.3)

Такой индекс показывает, во сколько раз возросла, если I >1 (уменьшилась, если I <1) стоимость продукции (товарооборота) отчетного периода по сравнению с базисным.

Разность числителя и знаменателя (Σp₁q₁ – Σp₀q₀) показывает, на сколько рублей увеличилась (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным.

Индекс физического объема продукции (I_q) – это индекс количественного показателя. В этом индексе индексируемой величиной будет количество продукции в натуральном выражении, а весом (соизмерителем) – цена.

Формула индекса примет следующий вид:

. (6.4)

Индекс цен (I_p) – это индекс качественного показателя.

Индекс цен определяется по формуле

. (6.5)

Немецкие ученые Г. Пааше и Э. Ласпейрес предложили разные формулы для расчета этих индексов в зависимости от используемых соизмерителей.

Для индексов Пааше соизмерителями являются параметры текущего периода, для индексов Ласпейреса – параметры базисного периода.

Пример 6.1

Рассмотрим применение индексного метода для изучения динамики сложных статистических совокупностей по данным табл. 6.1 о ценах и реализации товаров за два периода.

Таблица 6.1

Товар	Единица измерения	I период	II период	Индивидуальные индексы
Цена за ед. измерения, руб. (р0)	Количество (q0)	Цена за ед. измерения, руб. (р1)	Количество (q1)	Цен	Физического объема
А	т					1,25	1,27
Б	м					1,0	1,25
В	шт.					0,67	1,5

 

При определении по данным табл. 6.1 статистических индексов первый период принимается за базисный, в котором цена единицы товара обозначается р₀, а количество – q₀.

Второй период принимается за текущий (или отчетный), в котором цена единицы товара обозначается р₁, а количество – q₁.

Индивидуальные (однотоварные) индексы табл. 6.1 показывают, что в текущем периоде по сравнению с базисным цена товара А повысилась на 25%, на товар Б осталась без изменений, а на товар В снизилась на 33%. Количество реализации товара А возросло на 27%, товара Б – на 25%, а товара В – на 50%.

Применим формулу Пааше для расчета агрегатного индекса цен по данным табл. 6.1:

или 113,9%, т.е. по данному ассортименту товаров цены повысились в среднем на 13,9%.

Разность числителя и знаменателя индекса цен показывает абсолютный прирост товарооборота за счет изменения цен:

руб.

Следовательно, повышение цен на 13,9% обусловило увеличение объема товарооборота в текущем периоде на 40000 руб. Величина этого показателя с противоположным знаком (-40000 руб.) характеризует перерасход денежных средств населением при покупке товаров по повышенным ценам.

Для определения индекса физического объема товарооборота применим формулу Ласпейреса

(6.6)

Поскольку в числителе формулы (6.6) содержится сумма стоимости реализации товаров в текущем периоде по неизменным (базисным) ценам, а в знаменателе – сумма фактической стоимости товаров, реализованных в базисном периоде в тех же неизменных (базисных) ценах, то данный индекс является агрегатным индексом товарооборота в сопоставимых (базисных) ценах.

Используем формулу (6.6) для расчета агрегатного индекса физического объема реализации товаров по данным табл. 6.1.

Числитель индексного отношения

руб.

Знаменатель индексного отношения

руб.

Подставляя полученные суммы в формулу (6.6), получаем

или 127,8%,

т.е. по данному ассортименту товаров в целом прирост физического объема реализации в текущем периоде составил в среднем 27,8%.

Разность числителя и знаменателя индексного отношения (6.6) представляет собой показатель, характеризующий прирост суммы товарооборота в текущем периоде по сравнению с базисным периодом в сопоставимых (базисных) ценах:

(6.7)

Применяя формулу (6.7) к данным табл. 6.1, вычислим сумму прироста товарооборота:

руб.,

т.е. в результате изменения физического объема реализации товара в текущем периоде получен прирост объема товарооборота в сопоставимых ценах на 62,5 тыс. руб.

Отношение значений и дает общий индекс товарооборота в текущих ценах:

, (6.8)

где – сумма фактического товарооборота текущего периода;

– сумма фактического товарооборота базисного периода.

Этот индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции (товарооборота) отчетного периода по сравнению с базисным.

Величина объема товарооборота равняется произведению количества проданных товаров на цены. Следовательно, индекс физического объема I_q, умноженный на индекс цен I_p, дает индекс товарооборота в фактических ценах I_qp:

I_pq= I_p×I_q. (6.9)

Наличие связи между этими индексами (6.9) дает возможность по известным двум находить третий индекс.

При использовании формулы (6.9) надо иметь в виду, что взаимосвязь образуется лишь при условии, когда соизмерители в индексах физического объема и цен используется на разных уровнях, т.е. один из индексов рассчитывается по формуле Ласпейреса, другой – по формуле Пааше.

Пример 6.2

Если в отчетном периоде товарооборот в фактических ценах возрос по сравнению с базисным периодом на 12%, а цены на реализованные товары снижены в среднем на 3%, то можно определить изменение объема продажи:

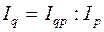. (6.10)

На основе исходной информации имеем: I_qp =1,12; I_p =0,97. Подставляя эти данные в формулу (6.10), определим индекс физического объема продажи товаров: I_q =1,12:0,97=1,154, или 115,4%, т.е. объем продажи увеличился в текущем периоде на 15,4%.

На основе формулы (6.9) можно по известным индексам товарооборота I_qp и объема продаж I_q определить индекс цен I_p:

. (6.11)

Пример 6.3

Если в отчетном периоде товарооборот вырос на 7%, а физический объем реализованной товарной массы увеличен на 10%, то для определения по этим данным изменения цен используется формула (6.11):

I_p =1,07:1,1=0,97,

т.е. цены в отчетном периоде снизились на 3%.

Другие индексы также тесно связаны меду собой. Так, индекс издержек производства – это произведение индекса себестоимости продукции на индекс физического объема продукции:

(6.12)

или

(6.13)

Пример 6.4

Если себестоимость увеличилась на 10%, а количество продукции снизилось на 8%, то индекс издержек производства будет равен величине

1,10 × 0,92 = 1,012, или 101,2%.

6.1.3. СРЕДНЕВЗВЕШЕННЫЕ ИНДЕКСЫ

В статистике применяется и другая форма индексов – средневзвешенные индексы. Их используют тогда, когда имеющаяся в распоряжении информация не позволяет рассчитать общий агрегатный индекс.

Средний индекс – это индекс, вычисленный как средняя величина индивидуальных индексов.

Средний арифметический индекс физического объема продукции рассчитывается по формуле

(6.14)

Весами в этой формуле является стоимость продукции базисного периода.

Средний гармонический индекс цен определяется из выражения

. (6.15)

Пример 6.5

Определите среднее снижение цен на товары в отчетном периоде по сравнению с базисным по следующим данным (табл. 6.2).

Таблица 6.2

Товар	Снижение цен в отчетном периоде по сравнению с базисным, %	Товарооборот в текущем периоде
А	-3
Б	-8

 

Решение

Воспользуемся формулой (6.15) для среднего гармонического индекса цен.

Индивидуальные индексы цен товаров А и Б будут иметь следующий вид:

i_рА = 100% – 3% = 97% = 0,97;

i_рВ =100% – 8% = 92% = 0,92.

Тогда

Следовательно, снижение цен по магазину в целом составило 5,26%.

6.1.4. ИНДЕКСЫ СТРУКТУРЫ

В практике часто приходится определять изменение средней величины индексируемого показателя, которое обусловлено взаимодействием двух факторов: изменением значения самого индексируемого показателя и изменением структуры явления. Так как на изменение среднего значения показателя оказывают воздействие два фактора, возникает задача определения степени влияния каждого из них на динамику средней.

Эта задача решается путем построения системы взаимосвязанных индексов среднего уровня, в которую входят три индекса: переменного состава, постоянного состава и структурных сдвигов.

Под изменением структуры явления понимается изменение доли отдельных групп единиц совокупности в общей их численности.

Индекс переменного состава – индекс, который выражает отношение средних уровней изучаемого явления, относящихся к разным периодам, и показывает изменение индексируемой величины с учетом изменения ее структуры.

Индекс постоянного (фиксированного) состава – индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо периода, и показывающий изменение только индексируемой величины.

Индекс структурных сдвигов – индекс, характеризующий влияние изменения структуры изучаемого явления на динамику среднего уровня этого явления.

Индекс цен переменного состава определяется из выражения

. (6.16)

Индекс цен фиксированного (постоянного) состава рассчитывается по формуле

. (6.17)

Индекс структурных сдвигов вычисляется как

. (6.18)

Система взаимосвязи индексов при анализе динамики средней цены имеет следующий вид:

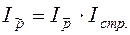. (6.19)

Здесь

– средняя цена единицы объема в базисном периоде;

– средняя цена единицы объема в отчетном периоде;

– расчетная средняя цена продажи единицы объема в текущем периоде по ценам базисного периода.

Пример 6.6

Определите изменения цен и структуру продажи по данным, представленным в табл. 6.3.

Таблица 6.3

Продажа товара в магазинах торговой ассоциации

Магазин	Базисный период	Текущий период	Расчетные графы
	Удельный вес реализации, %
Цена 1 кг, руб. p0	Кол-во кг q0	Цена 1 кг, руб. p1	Кол-во кг q1	ip	базисный	отчетный
					0,96	20,0	40,0
					0,97	40,0	30,0
					0,95	40,0	30,0
Σ

 

При анализе изменений лишь уровней цен (графа 2 и 4) исчисленные индексы i_p (графа 6) показывают, что в текущем периоде были снижены цены: в магазине №1 – на 4% (100 – 96%), в магазине №2 – на 3% (100 – 97%) и в магазине №3 – на 5% (100 – 95%).

Однако рассчитаны эти индексы безотносительно к объемам реализации.

Для определения изменения цен с учетом количества реализуемой продукции исчисляется индекс цен переменного состава

;

.

Таким образом, средняя цена реализации данного продукта в трех магазинах в целом выросла в текущем периоде на 2%. Рост цен равен = 0,8 руб. Население при покупке каждого кг данного продукта переплачивало по 0,8 рублей.

За счет действия каких факторов произошло это повышение (40,8 – 40)? Для ответа на этот вопрос надо рассмотреть данные о структуре реализации товара по магазинам. Вычисленные (в графе 7 и 8) удельные веса реализации показывают: с 20% до 40% вырос удельный вес продажи в первом магазине (более дорогом); а удельные веса продажи в магазинах 2 и 3 снизились. Как это повлияло на среднюю цену? Определим индекс влияния структурных сдвигов на изменение средней цены (за счет перераспределения массы проданных товаров).

, p₀ =40 руб.;

;

.

Из расчета следует, что структурные сдвиги в реализации объема данной продукции по отдельным магазинам вызвали повышение средней цены в текущем периоде на 6,25%. В абсолютном выражении это вызвало переплату населением при приобретении каждого килограмма продукции 2,5 рубля (42,5 – 40,0). Но в связи с тем, что в текущем периоде в каждом магазине имело место снижение цен, это также оказало влияние на уровень средней цены.

Индекс цен постоянного состава (за счет изменения только цен):

.

Он показывает, что в отчетном периоде цены в магазинах снизились в среднем на 4%. Это позволило населению при покупке каждого килограмма данной продукции сэкономить

руб.

Таким образом, рост цены продажи данного товара на 2% обусловлен, с одной стороны, ее увеличением на 6,25% за счет структурных сдвигов в объеме реализации, с другой стороны, – снижением в среднем на 4% цен в магазинах. В абсолютном выражении рост в текущем периоде средней цены одного килограмма на 0,8 рубля вызван увеличением цены на 2,5 рубля за счет структурных сдвигов и снижением в среднем на 1,7 рубля цен в магазинах (2,5 – 1,7 = 0,8). Рассмотренные индексы находятся в функциональной зависимости.

. (6.20)

. (6.21)

Для практического применения эта формула удобна тем, что на ее основе по любым двум известным индексам можно определить неизвестный индекс.

Пример 6.7

Если в текущем периоде по сравнению с базисным индекс цен переменного состава равен 1,025, а индекс цен постоянного состава равен 0,96, то это означает, что в ассортименте реализованных товаров произошли заметные структурные сдвиги:

,

т.е. структурные сдвиги составили 6,25%.

6.1.5. ТЕРРИТОРИАЛЬНЫЕ ИНДЕКСЫ

В статистической практике часто возникает потребность в сопоставлении уровней экономического явления в пространстве: по странам, экономическим районам, областям, т.е. в исчислении территориальных индексов. Тогда приходится решать вопрос, какие веса использовались при их исчислении. Например, если стоит задача сравнить цены в двух регионах – А и Б, то можно построить два индекса:

(6.22)

и

, (6.23)

где – индекс, в котором в качестве базы сравнения применяются данные по региону А;

– индекс, использующий в качестве базы сравнения данные по региону Б.

В методе стандартных весов значения индексируемой величины взвешиваются не по весам какого-то одного региона, а по весам области, экономического района, республики, в которых находятся сравниваемые регионы. Если в районе только два региона - А и Б, то индекс может вычисляться так:

. (6.24)

6.1.6. ИНДЕКСЫ СЕЗОННОСТИ

Для изучения сезонных колебаний показателей экономического развития используются индексы сезонности. Значительному колебанию в течение года подвержены денежное обращение, товарооборот, сельскохозяйственное производство и т.д. Это вызывает неравномерность использования трудовых ресурсов, напряженность в работе транспорта, хранилищ, потребления энергоресурсов и т.д. Для расчета индексов сезонности надо иметь помесячные данные минимум за три года.

Для каждого месяца рассчитывается средний уровень показателя , затем среднемесячный уровень . По этим данным определяется индекс сезонности I_с как процентное отношение средних для каждого месяца к общему среднемесячному уровню:

(6.25)

Пример 6.8

Имеются данные по реализации картофеля по месяцам на рынках города (тонн) за 3 года (табл. 6.4).

Таблица 6.4

Месяц Год	I	II	III	IV	V	VI	VII	VIII	IX	X	XI	XII
Средняя
Индекс сезонности	26.3	27.6	28.7	96.9	129.1	178.5	110.0	41.0	243.3	201.0	69.7	47.9

 

Определите индексы сезонности.

Решение

Для каждого месяца определяем среднее значение реализации картофеля по формуле средней арифметической:

январь: ;

февраль:

и т.д.

Расчетные данные сведены в таблицу.

Среднемесячное значение: = =261 т.

Тогда индексы сезонности для каждого месяца будут равны следующим величинам:

январь: I_S1 = =0,263, или 26,3%;

февраль: I_S2 = =0,276, или 27,6%

и т.д.

Расчет индексов сезонности показывает, что наименьший спрос приходится на январь-февраль, наибольший – на сентябрь-октябрь.

6.1.7. ИНДЕКСЫ ДОЛИ

Для определения доли расходов по i -тому товару в общем объеме потребительских расходов формулу Ласпейреса преобразуют к следующему виду:

, (6.26)

где i _p – индивидуальный индекс цен;

d_i = – доля расходов по i -тому товару.

Пример 6.9

Определите долю товаров А и В в общем объеме товарооборота магазина по имеющимся данным (табл. 6.5).

Таблица 6.5

Товар	Индекс цен 2005 г. в % к 2004 г.	Доля продаж данного товара в 2004 г., %
А	1,69	?
В	1,54	?
Ip	1,6

 

(Магазин реализует только два вида товаров.)

Решение

Индивидуальные индексы цен товаров А и В: i _pa=1,69; i _pв=1,54. Долю продажи товара А примем за d, тогда доля продажи товаров В составит величину (1- d).

По формуле (6.26):

1,6=1,69* d +1,54*(1- d).

Отсюда d =0,4=40%.

Таким образом, доля продажи товара А составила 40%, а товара В – 60% в общем объеме товарооборота магазина.

6.1.8. СИСТЕМА ИНДЕКСОВ

Базисные и цепные индексы можно свести в систему, которая определяет связь между ними.

Например, система индексов цен может быть построена так:

для базисных индексов – ; ; … , (6.27)

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: