 |
Характеристики портфеля ценных бумаг
|
|
|
|
Для уменьшения риска инвестор покупает на рынке не одну высокодоходную, но ненадежную ценную бумагу, а несколько ценных бумаг различного типа.
При этом инвестор следует пословице: «Никогда не клади все яйца в одну корзину». Дадим теоретическое обоснование данного принципа.
Все последующие рассуждения справедливы для стационарно развивающейся экономики, либо для промежутков времени ее стационарного развития. В нестационарном случае, например, в случае катастрофического кризисного развития экономики данные ниже математические модели не применимы.
Портфелем ценных бумаг инвестора называется совокупность некоторого количества ценных бумаг различного типа – векселей, акций нескольких корпораций, контрактов, опционов и т. д.
Предположение о стационарности позволяет описывать рынок ценных бумаг случайными величинами. В частности, значение эффективности Ri операции с i-ой ценной бумагой можно считать случайной величиной.
Пусть портфель инвестора содержит n ценных бумаг с эффективностями R1, R2, ¼, Rn. Предположим, что известны некоторые характеристики эффективностей:
1. Математическое ожидание случайной величины Ri, т. е. средняя ожидаемая эффективность i-ой бумаги.
mi=E(Ri)
2. Дисперсия (вариация) случайной величины Ri, оценивающая степень отклонения случайной величины Ri от ее математического ожидания:
 .
.
Дисперсия оценивает надежность ценной бумаги и является мерой финансового риска покупки i-ой ценной бумаги.
Среднеквадратическое (стандартное) отклонение s2 имеет ту же размерность, что и mi и Ri и равно:
 .
.
3. Ковариация двух случайных величин Ri и Rj равна:
 .
.
Она определяет связь между случайными величинами Ri и Rj, т. е. дает количественную оценку связи эффективности i-ой и j-ой ценной бумаги.
|
|
|
Ковариация двух случайных величин  имеет размерность равную произведению размерностей
имеет размерность равную произведению размерностей 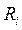 и
и  . Если разделить ковариацию
. Если разделить ковариацию  на среднеквадратические отклонения случайных величин
на среднеквадратические отклонения случайных величин 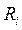 и
и  , то получится безразмерная величина - коэффициент корреляции.
, то получится безразмерная величина - коэффициент корреляции.
Коэффициент корреляции kij случайных величин Ri и Rj выражается через ковариацию следующим образом:
 или
или  .
.
Коэффициент корреляции является безразмерной величиной и изменяется в пределах от –1 до 1: 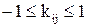 .
.
При kij=0 статистической связи между эффективностями i-ой и j-ой ценной бумагой нет.
При kij=1 эффективности i-ой и j-ой ценной бумаги коррелированны. Величина Rj линейно зависит от Ri, точнее:
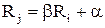 ,
,
где a, b – некоторые числа, причем b>0.
В этом случае Ri и Rj изменяются синхронно: росту Ri соответствует рост Rj, уменьшению Ri соответствует уменьшение Rj.
При  эффективности Ri и Rj антикоррелированы. Они линейно связаны, т. е.:
эффективности Ri и Rj антикоррелированы. Они линейно связаны, т. е.:
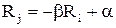 ,
,
где a, b – некоторые числа, причем b>0.
Обратим внимание на то, что при корреляции коэффициент при Ri в линейной связи положителен, а при антикорреляции этот коэффициент отрицателен.
Тогда Ri и Rj изменяются асинхронно или находятся в противофазе, т. е. увеличению Ri соответствует уменьшение Rj и, наоборот, уменьшению Ri соответствует увеличение Rj.
Описанных исходных данных достаточно для оценки рискованности портфеля.
Приведем конкретные примеры некоррелированных (независимых), коррелированных и антикоррелированных ценных бумаг (см. рис 6.1.-6.6.).

На рис 6.1. представлено облако измерений эффективностей R1, R2 двух независимых ценных бумаг. Центр масс этого облака имеет координаты (m1, m2), где m1=12,28 - математическое ожидание эффективности первой ценной бумаги, m2=14,95 - математическое ожидание эффективности второй ценной бумаги. Средний доход второй ценной бумаги m2 больше чем первой m1 (m1 < m2). Разброс статистических данных вдоль оси OX определяется дисперсией s12=2,75, вдоль оси OY дисперсией s22=17,31. Вдоль оси OY разброс больше, чем вдоль оси OY (s22>s12). Это означает, что вторая бумага будет более рискованной, но вторая ценная бумага будет и более доходной. Форма облака измерений характеризуется коэффициентом корреляции. Кругообразной форме облака измерений соответствует коэффициент корреляции близкий к нулю. В нашем случае коэффициент корреляции равен k12=-0,3211 и облако измерений близко к кругообразной форме.
|
|
|

На рис 6.2. представлено облако измерений эффективностей R1, R2 двух коррелированных ценных бумаг. Для данного облака измерений коэффициент корреляции равен k12=0,9947. Он близок к единице и облако измерений вырождается в отрезок возрастающей прямой  .
.

На рис 6.3. представлено облако измерений эффективностей R1, R2 двух антикоррелированных ценных бумаг. Для R1 и R2 коэффициент корреляции равен k12=-0,9969. Он близок к -1 и облако измерений вырождается в отрезок убывающей прямой 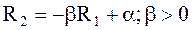 .
.
На рис 6.4.-6.6. представлены временные ряды эффективностей R1, R2 двух ценных бумаг.
Если коэффициент корреляции близок к нулю, то временные ряды эффективностей R1, R2 двух ценных бумаг ведут себя независимо друг от друга (см. рис. 6.4.).

Если коэффициент корреляции близок к 1, то временной ряд R2 получается из ряда R1 (в соответствии с формулой 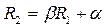 ) в результате сдвига графика R1 по оси OY на
) в результате сдвига графика R1 по оси OY на  и изменении масштаба по оси OY: при
и изменении масштаба по оси OY: при  растяжения графика вдоль OY, при
растяжения графика вдоль OY, при  сжатия графика вдоль OY (см. рис. 6.5.).
сжатия графика вдоль OY (см. рис. 6.5.).

Если коэффициент корреляции близок к -1, то временной ряд R2 получается из ряда R1 (в соответствии с формулой  ) в результате сдвига по оси OY на
) в результате сдвига по оси OY на  , зеркального отражения относительно оси ОХ и изменении масштаба по оси OY: при
, зеркального отражения относительно оси ОХ и изменении масштаба по оси OY: при  растяжения графика вдоль OY, при
растяжения графика вдоль OY, при  сжатия графика вдоль OY (см. рис. 6.6.).
сжатия графика вдоль OY (см. рис. 6.6.).

Всякой ценной бумаге может быть поставлена в соответствие пара чисел (s, m), где s оценивает риск, m – эффективность ценной бумаги.
Удобно рассматривать пары чисел (si, mi), соответствующие различным ценным бумагам, как точки на плоскости «риск – эффективность» (см. рис. 6.7).
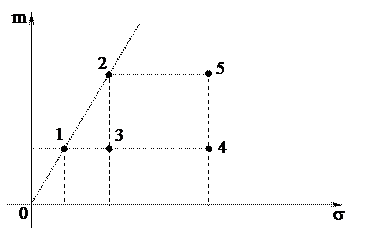
Рис. 6.7.
Сравнивая ценные бумаги 1, 3, 4, очевидно следует выбрать бумагу 1, так как для нее при одной и той же эффективности риск меньше. Сравнивая 2 и 3 (или 4 и 5), очевидно следует выбрать 2 (или 5), так как при одном и том же риске эффективность больше.
|
|
|
Без дополнительной информации невозможно сделать выбор только между 1 и 2 лежащими на одной прямой, проходящей через начало координат. Действительно, в этом случае увеличение риска приводит к пропорциональному увеличению эффективности.
|
|
|


