 |
И рискованных вложениях (J. tobin)
|
|
|
|
Ценные бумаги, входящие в портфель инвестора, можно разделить условно на две группы. В первую группу войдут ценные бумаги, имеющие малый риск и умеренную доходность. Во вторую группу войдут ценные бумаги, имеющие большую доходность и соответственно больший риск. Бумаги, имеющие малую доходность и больший риск, очевидно, не следует включать в портфель.
К безрисковым ценным бумагам условно можно отнести государственные ценные бумаги. В частности, на рынке США это вексель казначейства (US Treasury Bill), расписки казначейства (US Treasury Notes), бона казначейства (US Treasury bonds). В условиях 1990-х годов в России вряд ли какую-нибудь ценную бумагу можно считать безрисковой. Для этого периода следует использовать модель Г. Марковица (H. Markowitz), изложенную выше в п. 7. Учитывая тенденции к стабилизации экономики России в начале XXI века, следует рассчитывать на актуальность использования при оптимизации портфеля инвестора модели Тобина Д. (J. Tobin). Модели Г. Марковица (H. Markowitz) и Тобина Д. (J. Tobin) справедливы для стационарного рынка, в кризисных ситуациях они имеют ограниченный круг применения.
Тобин Д. рассмотрел следующую предельную ситуацию, когда инвестор выделяет x0 денег на приобретение ценных бумаг с ожидаемой эффективностью r0 и нулевым риском. Остальные 1-х0 денег инвестор тратит на рискованные ценные бумаги с ожидаемой эффективностью mi большей, чем эффективность безрисковых бумаг r0, т.е. mi> r0 (i=1, 2,…, n).
Математическая постановка задачи следующая.
Требуется найти распределение средств инвестора х0, х1, х2,…, хn между безрисковыми и рискованными бумагами 1, 2, …, n такое, что выполняются следующие линейные ограничения:
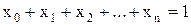(уравнение баланса) (8.1)
|
|
|
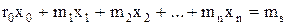(фиксация ожидаемой суммарной эффективности от портфеля акций на уровне ms) (8.2)
и минимизируется средний риск равный
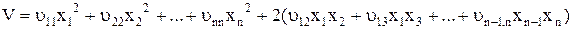(8.3)
В матричном виде условие задачи запишется для линейных ограничений:
1. Уравнение баланса
, (8.1')
где
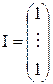‑ вектор столбец из 1;
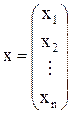‑ вектор столбец неизвестных;
I* ‑ транспонированный столбец или строка из 1.
2. Суммарная эффективность портфеля ms:
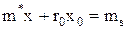, (8.2')
где
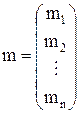‑ вектор столбец из эффективностей 1, 2, … n-ой ценной бумаги.
Минимизируемый риск равен квадратичной форме:
Ф(х)=х*Vх, (8.3)
где
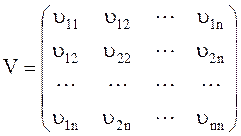‑ ковариационная симметричная матрица n´n.
Минимизируемая функция риска (8.3) или (8.3') включает только переменные х1, х2, хn и не включает переменной х0. Ограничения (8.1), (8.2) или (8.1'), (8.2') включает все переменные х0, х1, х2, хn. Удобно в ограничениях (8.1), (8.2) или (8.1'), (8.2') сразу избавится от переменной х0. Умножая ограничение (8.1') на число r0 и вычитая его из ограничения (8.2'), получим вместо двух ограничений одно ограничение содержащее только переменные х1, х2,… хn.
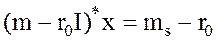(8.4)
Таким образом, задача оптимизации сводится к минимизации функции риска (8.3), (8.3') при одном ограничении (8.4).
Воспользуемся функцией Лагранжа для решения задачи
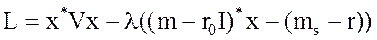, (8.5)
где
l – множитель Лагранжа.
Минимум достигается в критической точке, в которой частные производные обращаются в ноль, т.е.
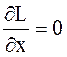
Первая частная производная дает n условий. Таким образом, получается n уравнений для определения n неизвестных хi.
После вычислений соответствующих производных получим уравнения:
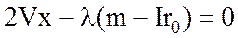(8.6)
Тогда, используя обратную матрицу V–1 для определения х, получим:
. (8.7)
Подставляя х из (8.7) в (8.4), получаем для множителя Лагранжа λ выражение:
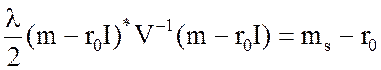
или, окончательно,
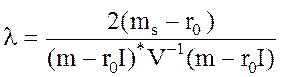. (8.8)
Тогда, избавляясь в (8.7) от множителя Лагранжа λ, получим явное выражение для х:
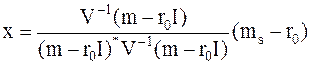. (8.9)
В формуле (8.9) в числителе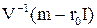 
– вектор столбец, в знаменателе 
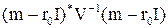– скаляр.
Формула (8.9) определяет количество средств Х, вкладываемых в рискованные бумаги. Количество средств, вкладываемых в безрискованные бумаги Х0 определяется по известным Х из уравнения баланса в виде
|
|
|
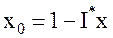(8.10)
или Х0 = 1 - Х1 - Х2 - …- Хn (8.11)
Важно, что величина ms входит в решение для х в виде скалярного множителя ms–r0. Таким образом, доля средств х, выделяемых на рискованные бумаги линейно зависит от ms–r0.
Структура рискованных вложений, определяемая отношением вложения хk в k-ую ценную рискованную бумагу к суммарному вложению в рискованные бумаги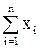 
, задается вектором:
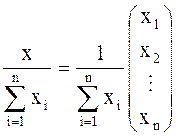(8.12)
и не зависит от суммарной доходности ms.
Действительно, учитывая, что из (8.9)
, (8.13)
получаем для структуры вложений из (8.12) и (8.13):
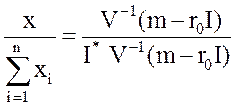. (8.14)
Оценим теперь суммарный риск для оптимального решения, т.е. найдем дисперсию оптимального портфеля ценных бумаг. Подставляя (8.9) в (8.3') получим для оценки суммарного риска дисперсию равную
(8.15)
Окончательно:
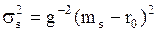, (8.16)
где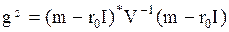 
‑ положительное число в силу знакоположительности матрицы ковариаций V и обратной к ней матрицы V-1. Отсюда следует, что среднеквадратическое отклонение риска σs линейно связано с ожидаемой эффективностью оптимального портфеля ms. Точнее из (8.16) имеем:
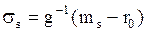, (8.17)
или
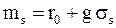. (8.18)
Таким образом, ожидаемая эффективность ms пропорциональна среднеквадратическому отклонению риска σs.
Пусть кроме линейных ограничений (8.1) и (8.2) имеются ограничения в виде неравенств 
, что соответствует запрету на получение денег в долг для покупки ценных бумаг.
Тогда, задача построения оптимального портфеля ценных бумаг, аналогично п. 7, может быть решена численными методами с использованием универсальных математических программных средств, Excel, Mathcad, Matlab, Maple или специальных программных средств, применяющих метод проекции градиента (Розена) и имеющихся в СЗАГС.
|
|
|
