 |
Вероятностные характеристики платежей
|
|
|
|
В разделе 2 получены связи между начальным капиталом S(0)=S0 и конечным капиталом S(t)=St, процентной ставке r и длительности сделки t формулы (2.2), (2.10), (2.12).
При длительности сделки в один год имеем:
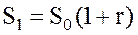(3.33)
При длительности сделки в t лет начисляются сложные проценты по формуле:
(3.34)
или непрерывные проценты по формуле:
(3.35)
В приведенных формулах величины начального капитала S0, конечного капитала St, процентной ставки r и длительности сделки t являются некоторыми числами, т. е. детерминированными величинами. Однако, в экономике очень часто возникает неопределенность. В этом случае экономические законы можно в ряде случаев успешно описывать не детерминированными, а случайными величинами. В частности, процентная ставка далеко не всегда может быть задана каким-то одним конкретным числом. Однако предполагается, что известны некоторые вероятностные характеристики ставки процента. Тогда, процентная ставка r может быть принята за случайную величину с известной функцией распределения. Таким образом, возникают две проблемы:
при известной функции распределения процентной ставки r:
· найти статистические свойства конечного капитала St при условии, что известен начальный капитал S0,
· найти статистические свойства начального капитала S0 при условии, что известен конечный капитал St.
Прежде чем приступать к решению проблем, опишем статистические свойства процентной ставки r. Приведем необходимые сведения из теории случайных величин.
Функцией распределения F(x) процентной ставки r называется вероятность того что случайная процентная ставка r принимает значения меньше x, т. е. F(x)=P(r<x), где P(*) – вероятность события *.
Функцией распределения F(x) обладает свойствами:
|
|
|
1. F(x) изменяется в пределах от 0 до 1, т.е. 
, причем 
и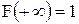 
;
2. F(x) монотонно возрастает;
3. Вероятность попадания случайной величины (процентной ставки r) на отрезок [ a, b ] равна:
Плотностью функции распределения называется производная от функции распределения.
Плотность функции распределения обладает свойствами:
1. 
так как 
возрастающая функция;
2. 
;
3. Вероятность попадания случайной величины на отрезок 
равна:
;
4. 
.
Применим приведенные сведения для оценки вероятностных характеристик накопленного вклада. Рассмотрим примеры.
Пример 51.
Процентная ставка r меняется ежемесячно и является случайной величиной с известной функцией распределения F(r). Вклад в банке равен $10000. Найти оценку вероятности того, что через год на счете будет больше $12000. Рассмотреть случай, когда процентная ставка r распределена по нормальному закону с математическим ожиданием 25 % = 0,25 и среднеквадратическим отклонением 10 %=0,1.
Решение.
Используем формулу (3.33), где S0 = $10 тыс., S1 = $12 тыс. и ставка r имеет известное распределение F(r).
Найдем вероятность того, что через год конечный капитал S1 превзойдет $12 тыс. Из формулы (3.33), используя преобразования неравенств, получим:
Таким образом, вероятность того, что конечный капитал превзойдет $12 тыс. при начальном капитале $10 тыс. равносильно вероятности того, что процентная ставка r превзойдет 20 % = 0,2.
Пусть теперь процентная ставка r распределена по нормальному закону с математическим ожиданием a =25 %=0,25 и среднеквадратическим отклонением σ = 10 % = 0,1. Для расчета вероятности используем нормированную нормальную функцию распределения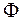 
с математическим ожиданием 0 и дисперсией 1 и заданную интегралом Лапласа:
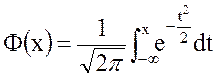
Для перехода к нормированной нормальной функции распределения центрируем случайную величину по формуле 
. Тогда, используя таблицы для вычисления интеграла Лапласа, найдем вероятность того, что через год конечный капитал S1 превзойдет $12 тыс.
|
|
|
Для вычисления интеграла Лапласа можно использовать функцию НОРМСТРАСП() из Excel.
Обобщим пример 51. Предположим, что начисление процентов происходит по схеме сложных процентов.
Пример 52.
Процентная ставка r меняется ежемесячно и является случайной величиной с известной функцией распределения F(r). Вклад в банке равен $10000. Найти оценку вероятности того, что через t=2, 3, 5 лет на счете будет больше $12000. Начисление процентов происходит по схеме сложных процентов. Рассмотреть случай, когда процентная ставка r распределена по нормальному закону с математическим ожиданием 25 % = 0,25 и среднеквадратическим отклонением 10 %=0,1.
Решение.
Используем формулу (3.34), где S0 = $10000, S1 = $12000 и ставка r имеет известное распределение F(r).
Найдем вероятность того, что через t лет конечный капитал S1 превзойдет $12 тыс. Из формулы (3.34), используя преобразования неравенств, получим:
При длительности сделки t=2, 3, 5 лет имеем соответственно:
Окончательно, используя для вычисления функции Лапласа таблицы или функцию НОРМСТРАСП() из Excel, найдем вероятность того, что конечный капитал S1 превзойдет $12 тыс. за 2, 3, 5лет соответственно:
Таким образом, вероятность того, что конечный капитал превзойдет $12 тыс. при начальном капитале $10 тыс. за 2, 3, 5 лет соответственно равна 0,938899; 0,969549; 0,98336.
Обобщим примеры 51, 52. Предположим, что начисление процентов происходит по схеме непрерывных процентов.
Пример 53.
Процентная ставка r меняется ежемесячно и является случайной величиной с известной функцией распределения F(r). Вклад в банке равен $10000. Найти оценку вероятности того, что через t=2, 3, 5 лет на счете будет больше $12000. Начисление процентов происходит по схеме непрерывных процентов. Рассмотреть случай, когда процентная ставка r распределена по нормальному закону с математическим ожиданием 25 % = 0,25 и среднеквадратическим отклонением 10 %=0,1.
Решение.
Используем формулу (3.35), где S0 = $10000, S1 = $12000 и ставка r имеет известное распределение F(r).
Найдем вероятность того, что через t лет конечный капитал S1 превзойдет $12 тыс. Из формулы (3.35), используя преобразования неравенств, получим:
При длительности сделки t=2, 3, 5 лет имеем соответственно:
|
|
|
Окончательно, используя для вычисления функции Лапласа таблицы или функцию НОРМСТРАСП() из Excel, найдем вероятность того, что конечный капитал St превзойдет $12 тыс. за 2, 3, 5лет соответственно:
Таким образом, вероятность того, что конечный капитал превзойдет $12 тыс. при начальном капитале $10 тыс. за 2, 3, 5лет соответственно равна 0,9439; 0,97077; 0,98363.
Сравнивая вероятности из примера 52 и 53, видим, что вероятность накопления капитала по непрерывным процентам больше.
Наиболее полное представление о случайной величине даёт функция распределения или плотность функции распределения. Во многих экономических приложениях можно ограничиться численными характеристиками случайной величины. Наиболее важными из них являются математическое ожидание и дисперсия. Они являются мерой среднего ожидаемого значения случайной величины и мерой разброса, рассеивания случайной величины.
Математическое ожидание определяет среднее ожидаемое значение случайной величины и равно:
,
где r - значение случайной величины,
f(r) dr – вероятность значения r случайной величины.
Свойства математического ожидания:
1. E(C) = C, где С – постоянная величина,
2. E(x + y) = E(x) + E(y), (3.36)
3. E(k x) = k E(x), где k – постоянный коэффициент.
Дисперсия определяет величину отклонения случайной величины от её математического ожидания и равна взвешенной сумме квадратов разности между значением случайной величины и её математическим ожиданием:
, (3.37)
где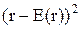 
- квадрат отклонения,
f(r) dr – вероятность такого отклонения.
Свойства дисперсии:
1. D(C) = 0, где С – постоянная величина.
2. D(k x) = k2 D(x), где k – постоянный коэффициент.
3. D(k x+b) = k2 D(x), где k – постоянный коэффициент,b - число.
Дисперсию удобно вычислять по теореме:
Дисперсия случайной величины x равна математическому ожиданию квадрата случайной величины минус квадрат математического ожидания, то есть:
(3.38)
Найдем статистические характеристики конечного капитала St при условии, что известен начальный капитал S0, и функция распределения процентной ставки r. Оценим математическое ожидание и дисперсию конечного капитала St для случая, когда начисляются простые проценты за год и сложные и непрерывные проценты за t лет.
|
|
|
Для математического ожидания в соответствии с (3.33), (3.34), (3.35) и (3.36) имеем:
E(S1) = E(S0 (1+r)) =S0 (1+ E(r));
E(St) = E(S0 (1+r)t) =S0 E((1 + r)t);
E(St) = E(S0 er t) =S0 E(er t).
Таким образом, задача сводится к вычислению математического ожидания E(r), E((1 + r)t) и E(er t).
В общем виде они равны соответственно:
(3.39)
Произведем вычисление до конца для случая равномерного распределения процентной ставки в пределах от a до b. В этом случае плотность функции распределения f(r) будет равна:
f(r)
при a< r< b
0, при r< a 1/(b-a)
0, при r> b
a b r
. рис.3.12.
График этой функции представлен на рис. 3.12.
Тогда, для интегралов (3.39) имеем:
(3.40)
Окончательно для математического ожидания конечного капитала St соответственно имеем:
1. простые проценты
(3.41)
2. сложные проценты
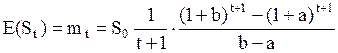(3.42)
3. непрерывные проценты
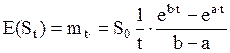(3.43)
Оценим дисперсию конечного капитала St для случая, когда начисляются простые проценты за год, сложные и непрерывные проценты за t лет.
В соответствии с (3.33), (3.34), (3.35) и (3.37) для дисперсий имеем:
D(S1) = S02 D(r),
D(St) = S02 D((1+r)t), (3.44)
D(St) = S02 D(er t).
Для вычисления дисперсии по формуле (3.38) нужно вычислить математические ожидания от квадратов случайной величины. При равномерном распределении имеем из (3.40) соответственно:
Отсюда для дисперсии получим соответственно:
(3.45)
Окончательно, в соответствии с (3.44), для дисперсии конечного капитала St соответственно имеем:
(3.46)
Совокупность формул (3.41), (3.42), (3.43) и (3.46) дают оценки математического ожидания и дисперсию конечного капитала St для случая, когда начисляются простые проценты за год, сложные и непрерывные проценты за t лет.
Найдем статистические характеристики начального капитала S0 при условии, что известен конечный капитал St, и функция распределения процентной ставки r. Оценим математическое ожидание и дисперсию начального капитала S0 для случая, когда начисляются простые проценты за год и непрерывные проценты за t лет.
Рассмотрим сначала случай, когда начисляются простые проценты за год. Из (3.33) находим начальный капитал:
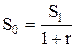(3.47)
Тогда математическое ожидание равно:
(3.48)
Окончательно для математического ожидания начального вклада получим:
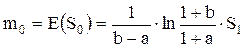
(3.49)
Дисперсия начального вклада из (3.44), (3.46) равна:
Воспользуемся теоремой (3.38) для вычисления дисперсии случайной величины 
. Дисперсия случайной величины равна математическому ожиданию квадрата случайной величины минус квадрат математического ожидания. Вычислим сначала в общем виде:
|
|
|
Для равномерного распределения получим:
Окончательно для дисперсии начального капитала S0 в случае равномерного распределения процентной ставки r от a до b имеем:
(3.50)
Рассмотрим теперь случай, когда непрерывные проценты начисляются t лет. Из (3.35) находим начальный капитал:
(3.51)
Тогда математическое ожидание аналогично (3.40) и (3.43) равно:
(3.52)
Аналогично (3.45) и (3.46) для дисперсии начального капитала S0 в случае равномерного распределения процентной ставки r от a до b имеем:
(3.53)
Таким образом, в данном разделе построены статистические характеристики начального и будущего капитал при известной функции распределения процентной ставки.
Задача 13.
Найти статистические характеристики начального капитала S0 при условии, что известен конечный капитал St, и функция распределения процентной ставки r. Оценить математическое ожидание и дисперсию начального капитала S0 для случая, когда начисляются сложные проценты за t лет. Рассмотреть случай равномерного распределения процентной ставки в пределах от a до b.
Ответы:
|
|
|
