Расчет Н нормы рентабельности (индекса доходности) инвестиционного проекта

	процентная ставка r=	10,00%
Даты	Значения (млн. руб.)	инвестиции C-	доходы C+	дисконт. сумма доходов	Н
01.01.2008	-100	100,0
01.01.2009	-150	150,0
01.01.2010				0,00	0,000
01.01.2011				45,07	0,191
01.01.2012				86,04	0,364
01.01.2013				123,27	0,522
01.01.2014				157,12	0,665
01.01.2015				187,90	0,795
01.01.2016				215,87	0,913
01.01.2017				241,30	1,021
01.01.2018				264,41	1,119
01.01.2019				285,43	1,208
01.01.2020				304,53	1,289

 

На рис 4.5 и в шестом столбце таблицы представлена зависимость нормы рентабельности H(t) от времени t при процентной ставке r=10 %. В момент времени 01.01.2017 она составляет Н=1,021. Это значение превышает единицу то, есть на 1 руб. инвестиций получено 1,021 руб. дохода, что соответствует времени окупаемости инвестиционного проекта.

 

Пример56. Оценка риска инвестиционного проекта.

 

Инвестиционный проект задан двусторонним потоком платежей. Соответствующий поток приведен в двух первых столбцах таблицы 4.3. Процентная ставка является случайной величиной, распределенной по нормальному закону с математическим ожиданием a = 10 % и среднеквадратическим отклонением σ = 3 %. Найти вероятность окупаемости инвестиционного проекта на момент времени t.

Решение.

Процентная ставка распределена по нормальному закону. Функция распределения нормально распределенной случайной величины с математическим

 

ожиданием a и среднеквадратическим отклонением σ имеет вид:

,

где для расчета вероятности P(r < x) используется нормированная нормальная функцию распределения 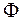с математическим ожиданием 0 и дисперсией 1 и заданная интегралом Лапласа:

.

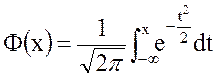Для перехода к нормированной нормальной функции распределения центрируем случайную величину по формуле . Для вычисления функции Лапласа можно использовать таблицы или функцию НОРМСТРАСП() из Excel.

Согласно п. 4.2 чистое современное значение NPV зависит от процентной ставки r и времени t, то есть NPV = NPV(r, t). Фиксируем время t. Если процентная ставка r является случайной величиной, то и современное значение NPV будет случайной величиной. Окупаемость проекта наступает, когда современное значение NPV становится больше нуля, т. е. окупаемости проекта соответствует событие NPV(r, t)>0. Найдем вероятность этого события:

,

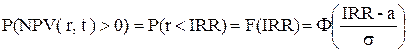где IRR – эффективная ставка проекта на момент t. Согласно п. 4.3 она является решением уравнения NPV(t, IRR) = 0.

Тогда, используя для вычисления интеграла Лапласа функцию НОРМСТРАСП() и функцию ЧИСТВНДОХ() для вычисления эффективной ставки IRR, найдем вероятность того, что инвестиционный проект окупится к моменту t. Результаты расчетов приведены в таблице 4.3 и проиллюстрированы рис 4.6.

 

Таблица 4.3.

Зависимость вероятности окупаемости от длительности проекта

Даты	Суммы	Эффективная ставка IRR	Вероятность окупаемости
01.01.2008	-100
01.01.2009	-150
01.01.2010
01.01.2011		-45,78%	0,000000
01.01.2012		-22,34%	0,000000
01.01.2013		-9,15%	0,000000
01.01.2014		-1,04%	0,000117
01.01.2015		4,26%	0,027946
01.01.2016		7,89%	0,240954
01.01.2017		10,46%	0,560307
01.01.2018		12,32%	0,780335
01.01.2019		13,71%	0,891625
01.01.2020		14,75%	0,943478
01.01.2021		15,56%	0,968051
01.01.2022		16,18%	0,980370

 

 

 

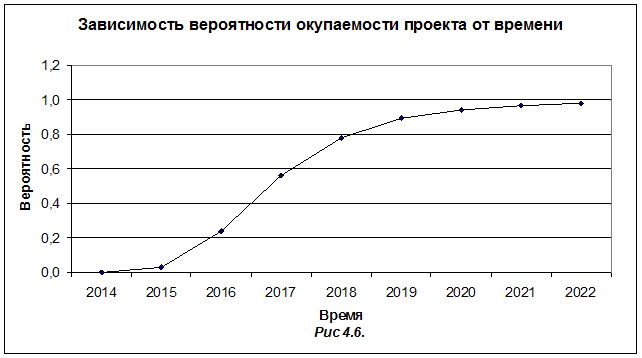
Таким образом, если процентная ставка является случайной величиной, распределенной по нормальному закону с математическим ожиданием a = 10 % и среднеквадратическим отклонением σ = 3 %, то вероятность окупаемости проекта на 2017 год равна 0,56 на 2018 и 2019 годы она возрастет и будет равна соответственно 0,78; 0,89.

 

 

 

МОДЕЛИРОВАНИЕ РИСКОВ НА РЫНКЕ ЦЕННЫХ БУМАГ

Финансовый риск

Профессия финансиста столь же рискованна, как и профессия подводника, летчика или космонавта. Всякая финансовая операция связана с возможным либо обогащением, либо разорением. Введем понятие финансового риска и построим его количественные характеристики.

Финансовая операция (сделка) называется рискованной, если ее эффективность недетерминирована, т. е. не известна в момент заключения сделки.

В этом случае эффективность финансовой сделки является случайной величиной и зависит от случайных обстоятельств.

Другими словами рискованную финансовую сделку нельзя характеризовать каким-либо одним значением эффективности.

Рискованной сделке соответствует целый ансамбль возможных значений эффективности, реализующихся с той или иной вероятностью.

Если удается получить некоторые вероятностные характеристики эффективности сделки, то может быть поставлена задача ограничения или минимизации риска при заданном уровне доходности сделки.

Практически любая финансовая сделка является рискованной, лишь некоторые финансовые операции с некоторой степенью условности можно считать безрисковыми. Например, государственные процентные бумаги экономически развитых стран.

Построим некоторые количественные характеристики риска. Чтобы разговор не был слишком абстрактным, рассмотрим финансовые операции с акциями, эффективность которых может характеризоваться величиной:

, (5.1)

где

С₀ – цена покупки акции в момент 0;

С₁ – цена продажи в момент 1;

d – дивиденды, полученные за время от начального момента 0 до конечного момента 1.

Заметим, что аналогичный критерий эффективности может быть построен для других ценных бумаг, например, для облигаций. Тогда, С₀ – цена покупки облигации, С₁ – цена продажи облигации, d – доход от купонов.

Эффективность R, как уже отмечалось выше, является случайной величиной. Самой полной информацией о случайной величине была бы плотность функции распределения этой величины. Для дальнейших исследований достаточно более скромной информации о случайной величине. Будем считать, что известны некоторые вероятностные характеристики (например, из анализа прошлого фондового рынка), позволяющие построить математическое ожидание m эффективности:

m=E(R), (5.2)

где E() обозначает математическое ожидание, т. е. осреднение по всему ансамблю возможных значений.

Степень отклонения случайной эффективности R от ее математического ожидания m характеризуется дисперсией (вариацией), равной:

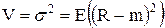, (5.3)

где

– вариация или дисперсия;

– среднеквадратическое отклонение.

Дисперсия или вариация всегда больше нуля. Размерность математического ожидания совпадает с размерностью случайной величины. Размерность дисперсии случайной величины равна квадрату размерность самой случайной величины. Размерность среднеквадратического отклонения случайной величины совпадает с размерностью случайной величины.

Величина дисперсии (вариации) является количественной оценкой степени рискованности сделки, чем больше дисперсия, тем более рискованной является финансовая сделка. В предельном случае для безрисковых операций дисперсия равна нулю.

 

Неравенство Чебышева

Для оценки рискованности операции и выбора средств ограничения риска может быть полезна теорема Чебышева для случайных величин. В простейшем случае она связывает меру отклонения случайной величины R от ее математического ожидания m с ее дисперсией s². Точнее она формулируется так.

Теорема Чебышева

Вероятность того, что случайная величина R отклонится от своего математического ожидания m больше, чем заданное значение d, не превосходит ее дисперсии s², деленной на d², т. е.:

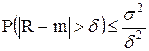, (5.4)

где Р(*) обозначает вероятность события *.

Воспользуемся теоремой Чебышева для решения следующей задачи.

Пример 57.

Господин А делает заем под процент r и под залог недвижимости. На полученные взаймы деньги господин А покупает акции. Какова вероятность того, что господин А не сможет вернуть долг и лишится недвижимости?

Решение.

Будем считать, что эффективность R покупаемых господином А акций характеризуется математическим ожиданием доходности m и дисперсией s². Отметим, что сделка имеет смысл, если m>r. Однако вероятность разорения все равно остается. Событие, которое приводит к разорению инвестора, состоит в следующем:

R<r, (5.5)

т. е. эффективность вложения в акции R меньше r процентной ставки займа. Здесь R – случайная величина, а r – детерминированная величина. Из (5.5) следует . Тогда, для вероятности имеем:

.

Далее воспользуемся неравенством Чебышева (5.4):

.

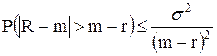Окончательно, для вероятности разорения инвестора имеем неравенство:

.

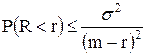Таким образом, вероятность разориться не превосходит величины . Если инвестор хочет, чтобы шанс разориться не превышал , то достаточно выполнения условия: или , т. е. ожидаемая эффективность вложения в акции должна быть больше процентной ставки займа плюс три среднеквадратических отклонения 3s. При этом вероятность разорения будет менее .

Хеджирование

Хеджирование (hedging) – любая схема, позволяющая исключить или ограничить риск финансовых операций, связанных с ценными бумагами.

Для иллюстрации хеджирования рассмотрим следующий модельный пример.

Инвестор-кредитор А собирается вложить сумму С в дело под r процентов. Ожидаемый доход равен R=Cr. Однако операция инвестору представляется рискованной, и он решает приобрести страховой полис, гарантирующий выплату определенной суммы в случае провала сделки.

Для этого сумму С инвестор разделяет на две части: Cx он вкладывает в сделку и, C(1-x) он тратит на страховку, где х, 1-х – доля суммы, потраченная на финансовую сделку и страховой полис соответственно. Возможны два варианта развития событий.

Вариант 1.

Сделка оказалась удачной. В результате получен доход:

.

Вариант 2.

Сделка не удалась. Инвестор получает страховую выплату в размере , где q – отношение страхового возмещения к цене полиса. Тогда полученный доход равен:

.

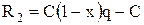Очевидно, логично выбрать х так, чтобы доход в обоих случаях был одинаков R₁=R₂. Решив линейное уравнение, получим:

.

При этом доход будет равен:

.

Таким образом, данная схема хеджирования исключает неопределенность, при этом эффективность сделки снижается с r до .

Рассмотрим численный пример. Пусть r=20 % = 0,2, а q = 50. Тогда доля средств, отпускаемых на сделку, будет равна: .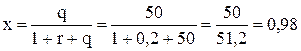

Доля средств на страховку будет равна 1–х=0,02. Эффективность уменьшается с r=20 % до .

Таким образом, за счет небольшого уменьшения эффективности с 20 % до 17 % удастся уменьшить финансовый риск сделки.

ПОРТФЕЛЬ ЦЕННЫХ БУМАГ

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: