Прямой статистический метод

Для построения портфеля ценных бумаг требуются оценки математических ожиданий эффективности ценных бумаг и ковариационная матрица эффективностей ценных бумаг.

Если множество ценных бумаг не велико. Например, из множества ценных бумаг выбрано порядка 10÷30 ценных бумаг, то возможен прямой расчет ожидаемой доходности и ковариационной матрицы.

Напомним некоторые особенности статистических оценок параметров. Не вдаваясь в тонкости математической статистики, отметим, что точность оценок тем выше, чем больше имеется исходных статистических данных, и тем ниже, чем больше число оцениваемых величин. Таким образом, точность статистических оценок зависит от соотношения объема статистических данных и количества оцениваемых параметров. Точнее объем статистических данных должен быть больше количества оцениваемых параметров. В противном случае, когда число оцениваемых параметров сравнимо с объемом статистических данных статистическим оценкам нельзя доверять.

Рассчитаем число оцениваемых параметров и объем выборки. Пусть в портфель включено n ценных бумаг. Тогда требуется оценить n математических ожиданий m₁, m₂, … m_n, и моментов второго порядка симметричной ковариационной матрицы v_{i j} (i = 1, 2, … n; j = 1, 2, … n). Общее число оцениваемых параметров равно:

Определим объем выборки. Предположим, что для каждой ценной бумаги ежеквартально можно найти эффективность R (см. (5.1)). Период времени, за который можно использовать статистические данные о курсовой стоимости и дивидендах акций не более 25 лет. Дело в том, что экономические условия и даже сам список ведущих компаний за период более 25 лет слишком сильно изменяются, чтобы столь устаревшие данные считать представляющими ту же генеральную совокупность.

При этом длительность ежеквартальных временных рядов R эффективности акций, имеющих смысл для статистической обработки, t = 4·25 = 100. Таким образом, объем выборки для оценок эффективностей n ценных бумаг равен:

M = n·t = 100·n

Для статистической оценки параметров требуется выполнения хотя бы самого слабого ограничения: длина выборки M должна быть больше числа оцениваемых параметров N (M>N). В результате решения неравенства M>N получим, что это возможно при числе ценных бумаг меньше 193. Чтобы получить более достоверные оценки, длина выборки M должна быть в два раза больше числа оцениваемых параметров N (M>2 N). Отсюда, число оцениваемых бумаг должно быть меньше 93.

Таким образом, прямой статистический подход используется для вычисления оценочной доходности ценных бумаг и ковариаций между «самими главными» акциями. При определении индекса Доу-Джонса используется информация о 30 акциях. При этом нужно оценить 30 математических ожиданий и 465-элементов ковариационной матрицы. Итого получается 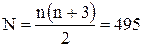-оцениваемых параметров.

Соответствующий объем выборки для оценок n=30 ценных бумаг равен M=n·t=100·n = 3000. Тогда, объем выборки M =3000, что вполне достаточно для оценки N=495 параметров.

В общем случае, число ведущих компаний, акций которых котируются на биржах США и составляют основную, по общей стоимости, часть рынка обычно оценивают в n = 500. Такое число учитывается в Standard and Poor’s Index. Для этого случая число оцениваемых параметров равно , а длина выборки существенно меньше M=n·t=100·n = 5 10⁴.

Очевидно, что оценить N=1,2575·10 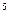параметров по выборке объемом M=5·10 прямым статистическим методом невозможно.

Однако финансовый аналитик обязан давать рекомендации по возможно большему числу компаний, ценные бумаги которых котируются на фондовом рынке.

 

Метод ведущих факторов

В экономической жизни все взаимосвязано, но есть факторы, которые влияют сразу на все показатели. Таких факторов может быть несколько. Например, цены на энергоносители, недвижимость, кредиты и т. д. Рассмотрим один из таких ведущих факторов, не определяя пока его природу.

Пусть R - эффективность i-ой ценной бумаги, F-ведущий фактор фондового рынка. Будем считать, что эффективность всех вложений зависит от него. Простейшая зависимость линейна (см. рис. 9.1.). Примем гипотезу:

+ε_i, (9.1)

где ε_i - случайные погрешности линейного представления эффективности i-ой ценной бумаги R через ведущий фактор F. Предполагается, что математические ожидания погрешностей равно нулю E(ε_i) = 0. и погрешности ε_i и ε_j попарно взаимно некорелированы E(ε_i · ε_j) = 0 и некорелированы с ведущим фактором E(ε_i · F) = 0.

Рис.9.1.

 

Определить постоянные значения и можно по синхронным измерениям эффективностей R₁, R₂, … R_n, и ведущего фактора F методом наименьших квадратов, т. е. построить линейную парную регрессию (см. приложение).

Тогда, из (9.1) при известных , , известном математическом ожидании m_F и дисперсии ведущего фактора F и известной дисперсии погрешности 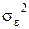могут быть получены оценки для математических ожиданий эффективностей ценных бумаг:

(9.2)

Вычитая из (9.1) формулу (9.2) получим:

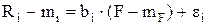
Следовательно, дисперсия эффективности ценной бумаги будет равна:

(9.3)

Для ковариаций соответственно получим:

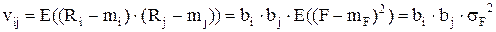(9.4)

Таким образом, полученные математические ожидания эффективностей ценных бумаг (9.2) и элементы ковариационной матрицы (9.3) и (9.4) могут быть использованы для построения оптимальных портфелей ценных бумаг.

ЗАКЛЮЧЕНИЕ

 

В заключении отметим, что в СЗАГС разработаны и используются в учебном процессе специализированные программы для финансовых расчетов и оценок финансовых рисков. Кроме того, в СЗАГС имеются методики, позволяющие решать указанные выше задачи универсальными программными математическими средствами Matcad, Matlab и Maple.

ПРИЛОЖЕНИЕ

⇐ Предыдущая9101112131415161718Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: