 |
Линейная регрессия. Парная линейная регрессия
|
|
|
|
Пусть имеются две случайные величины X и Y. Можно ли считать их линейно связанными, т. е. можно ли Y считать линейной функцией от X? Каковы коэффициенты в этой линейной функции?
Сначала будем считать, что математические ожидания x и y равны нулю, ◦т. е.:
(П.14)
Это не очень большое ограничение, так как в случае отличия от нуля математических ожиданий 
и 
, всегда можно перейти к центрированным случайным величинам 
, 
. Для них математическое ожидание будет равно нулю.
Найдем коэффициент m, обеспечивающий наилучшую линейную связь между y и x:
y = mּx (П.15)
Коэффициент m можно выбрать так, чтобы дисперсия разности (невязки)
(П.16)
была минимальной.
Таким образом, m выбирается из минимума функции
(П.17)
Задача нахождения m, обеспечивающего min функции (П.17), типичной задачей метода наименьших квадратов. Для её решения распишем функцию (П.17)
где 
- дисперсия x,
- дисперсия y,
- ковариация x и y,
- коэффициент корреляции между x и y.
Коротко имеем:
(П.18)
Для нахождения m минимизирующего функцию Φ(m) приравняем к нулю производную:
отсюда 
(П.19)
Таким образом, уравнение линейной регрессии для случайных величин с нулевым математическим ожиданием имеет вид:
(П.20)
В общем случае при замене x, y на x- 
, y- 
имеем:
,
После элементарных преобразований уравнения линейной регрессии может быть записано в виде:
(П.21)
где ; 
(П.22)
- математические ожидания x, y;
- дисперсия x, y;
- коэффициент корреляции между x и y.
Погрешность определения линейной регрессии определяется дисперсией невязки:
(П.23)
Удобно использовать относительное значение дисперсии:
(П.24)
Качество линейной регрессии тем лучше, чем ближе к нулю величина 
. При коэффициенте корреляции 
получим 
и тогда между y и x имеется точная линейная связь.
|
|
|
Множественный регрессионный анализ
Предполагается, что между величиной y и величинами x1, x2, …, xn имеется линейная связь, т. е.:
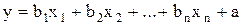(П.25)
Известен ряд измерений y(t), x(t), …, xn(t), где t=1,2,…,m. Как найти коэффициенты b1, b2, …, bn, a?
Для их определения воспользуемся методом наименьших квадратов. Найдем невязку:
(П.26)
Выберем коэффициенты a, b1, b2, …, bn, так, чтобы сумма квадратов невязки была минимальной:
(П.27)
Для нахождения минимума найдем частные производные по b1, b2, …, bn, a и приравняем их к нулю.
…………………………………………………………….. (П.28)
Отсюда получаем систему линейных уравнений для определения параметров в матричном виде:
(П.29)
или в виде:
(П.30)
Система из n+1 линейных уравнений для определения n+1 неизвестного может быть решена, если определитель системы будет отличен от нуля. Для решения этих уравнений имеются специальные программы в Excel, Matlab, Maple и др.
При n=1 получается случай парной линейной регрессии y=bּx+a. После аналитического решения системы (П.30) в случае n=1 для коэффициентов линейной регрессии получим:
(П.31)
(П.32)
Формулы (П.31) и (П.32) являются дискретным аналогом формул линейной регрессии (П.21) и (П.22).
В Excel имеются функции для расчета математического ожидания, дисперсии, ковариации, корреляции и функция для расчета линейной регрессии.
РАЗДЕЛ Ш. СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Основная литература.
1. Берндт Эрнст Роберт. Практика эконометрики: классика и современность, для студентов вузов обучающихся по специальности 060000 «экономика и управление». (Пер. с англ под ред. проф. С. А. Айвазяна), серия «зарубежный учебник», ‑ М.: ЮНИТИ-ДАНА, 2005. - 863 с.
1. Виленский П. Л., Лившиц В. Н., Смоляк С. А. Оценка эффективности инвестиционных проектов. ‑ М.: Изд-во Дело, 2002. - 888 с.
2. Гитман Л. Дж., Джонк М. Д. Основы инвестирования. Пер. с англ. ‑ М.: Дело, 1999. - 1008 с.
|
|
|
3. Дубина А. Г., Орлова С. С., Шубина И. Ю., Хромов А. В. Excel для экономистов и менеджеров. – СПб.: Питер, 2004. - 295 с.
4. Клоков В. И. Финансовые риски. Методическое пособие. ‑ СПб.: Изд-во СЗАГС, 2002. - 60 с.
5. Клоков В. И. Инвестиции, учебно- методический комплекс. ‑ СПб.: Изд-во СЗАГС, 2004. - 32 с.
6. Клоков В. И. Финансовый рынок: расчет и риск, учебно-методический комплекс. ‑ СПб.: Изд-во СЗАГС, 2005. - 94 с.
7. Клоков В. И. Финансовые рынки, учебное пособие. ‑ СПб.: Изд-во. СЗАГС, 2005. -96 с.
8. Мельников А. В., Попова Н. В., Скорнякова В. С. Математические методы финансового анализа. ‑ М.: Изд-во Анкил, 2006. - 440 с.
9. Первозванский А. А., Первозванская Т. Н. Финансовый рынок: расчет и риск. – М.: Инфра-М, 1994. - 192 с.
10. Печенежская Н. А. Финансовая математика: сборник задач. ‑ Ростов н/Д: Изд-во Феникс, 2008. - 188 с.
11. Просветов Г. И. Управление рисками: задачи и решения. Учебно-практическое пособие. ‑ М.: Изд-во Альфа-Пресс, 2008. - 416 с.
12. Самаров К. Л. Финансовая математика. Сборник задач с решениями. Учебное пособие. ‑ М.: Изд-во Альфа-М, Инфра-М, 2009. - 90с.
13. Уотшем Терри.Дж., Паррамоу Кейт. Количественные методы в финансах ‑ М., Финансы, изд. ЮНИТИ, 1999. -528 с.
14. Финансовый менеджмент. Теория и практика. – М.: Перспектива, 1999.-656 с.
15. Хеннигер Э., Крюгер Т. М. Руководство по изучению учебника «Основы инвестирования» Гитман Л. Дж., Джонк М. Д. Пер. с англ. ‑ М.: Дело, 1999. - 192 с.
16. Четыркин Е. М. Финансовый анализ производственных инвестиций. – М.: «Дело ЛТД», 1998. - 256 с.
17. Шапкин А. С., Шапкин В. С. Теория риска и моделирование рисковых ситуаций. Учебник. ‑ М.: Издательско-торговая корпорация «Дашков и К», 2006. -880 с.
18. Шарп Уильям Ф. и др. Инвестиции (университетский учебник). ‑ М.: ИНФРА-М, 1998. - 1028 с.
19. Экономико-математические методы и модели. Учебное пособие. – Минск: Изд-во БГЭУ, 1998. - 413 с.
20. Кузнецов Б.Т. Инвестиции учеб. пособие. 2-е изд., М. ЮНИТИ-ДАНА, 2010. – 623с.
Дополнительная литература.
1 Анискин Ю. П. Управления инвестициями. Учебное пособие по специальности «Менеджмент организации». ‑ М.: Изд-во ОМЕГА-Л, 2006. - 193 с.
2 Рубцов Б. Б. Современные фондовые рынки, учебное пособие для вузов. ‑ М.: Алпина Бизнес Букс, 2007. - 926 с.
3 Башарин Г. П. Начала финансовой математики. – М.: Инфра-М, 1997. - 160 с.
|
|
|
4 Капельян С. П., Левкович О. А. Основы коммерческих и финансовых расчетов. – Минск: НТЦ АПИ, 1999. -224 с.
5 Ковалев В. В. Финансовый анализ: Управление капиталом. Выбор инвестиций. Анализ отчетности. ‑ М.: Финансы и статистика, 1998. - 432 с.
6 Кириллов А. Л. Математика для управленцев. Курс лекций. ‑ СПб.: Изд-во СЗАГС, 2000. - 240 с.
7. Колемаев В. А. Математическая экономика. Учебник для вузов. ‑ М.: ЮНИТИ-ДАНА, 2002. -399 с.
8. Колемаев В. А. Математические методы и модели исследования операций. Учебник для студентов вузов обучающихся по специальности 088116 «Математические методы в экономике. ‑ М.: ЮНИТИ-ДАНА, 2008. - 592 с.
9. Колмыкова Л. И. Фундаментальный анализ финансовых рынков. ‑ СПб.: Питер, 2008. - 288 с.
10. Курзенев В. А. Основы математической статистики для управленцев. - СПб.: Изд-во СЗАГС, 2005. - 206 с.
11. Лабскер Л. Г. Вероятностное моделирование в финансово – экономической области. ‑ М.: Альпина Паблишер, 2002. -224 с.
12. Лобанов А. А., Чугунов А. В. Энциклопедия финансового риск – менеджмента. М.: Альпина Бизнес Букс, 2007. - 878 с.
13. Ширяев А. П. Основы стохастической финансовой математики. Т. 1, Факты. Модели, - 512 с., Т. 2 Теория, - 544 с., - М.: Фазис, 1998.
14. Ширяев А. П. Стохастические модели финансовой математики. - М., 2000.
15. Люу Ю-Д. Методы и алгоритмы финансовой математики. Пер. с англ., М., БИНОМ Лаборатория знаний, 2009. – 751с.
16. Markovitz H. M. Portfolio selection. // J. of Finances. V. 7. 1952. № 1. P. 77-91.
17. Tobin D. Liquidity preference as behavior toward risk. // Rev. of Econ. Studies. V. 25. 1958. № 1. P. 65-86.
РАЗДЕЛ IV. ПЛАНЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ
|
|
|
