 |
Задача с линейной целевой функцией и нелинейной системой ограничений
|
|
|
|
Пример 35. Найтиглобальные экстремумы функции L= 2 x 1 +х 2 при ограничениях: х 12+ х 22≤16, х 1, х 2≥0.
Решение. Область допустимых решений — часть окружности с радиусом 4, которая расположена в первой четверти
Рисунок 21
Линиями уровня целевой функции являются параллельные прямые с угловым коэффициентом, равным —2. Глобальный минимум достигается в точке О(0,0), глобальный максимум — в точке А касания линии уровня и окружности. Проведем через точку А прямую, перпендикулярную линии уровня. Прямая проходит через начало координат, имеет угловой коэффициент 1/2 и уравнение х 2= 1/2 х 1.
Решаем систему
откуда находим х 1= 
, х 2= 
, L= 
+ = 
.
Ответ. Глобальный минимум, равный нулю, достигается в точке О(0,0), глобальный максимум, равный , — в точке А (, ).
Задача с нелинейной целевой функцией и линейной системой ограничений
Пример 36. Найти глобальные экстремумы функции L= (x 1-2)2 + (х 2-3)2 при ограничениях:
Решение. Область допустимых решений — OABD. Линиями уровня будут окружности с центром в точке О1. Максимальное значение целевая функция имеет в точке D (9,0), минимальное — в точке O1(2,3). Поэтому L (D) = (9 - 2)2 + (0 - 3)2 = 58.
Рисунок 22
Ответ. Глобальный максимум, равный 58, достигается в точке D (9, 0), глобальный минимум, равный нулю, — в точке О1 (2,3).
Пример 37. Найти глобальные экстремумы функции
L = (х 1- 6)2 + (х 2 - 3)2 при ограничениях:
Решение. Область допустимых решений — OABD. Линии уровня представляют собой окружности с центром в точке О1(6,3). Глобальный максимум находится в точке О(0,0) как самой удаленной от точки О 1. Глобальный минимум расположен в точке Е, находящейся на пересечении прямой 3 x 1+2 х 2=15 и перпендикуляра к этой прямой, проведенного из точки О 1.
|
|
|
 |
Рисунок 23
Найдем координаты точки Е: так как угловой коэффициент прямой 3 х 1+2 х 2=15 равен —3/2, то угловой коэффициент перпендикуляра О 1 Е равен 2/3. Из уравнения прямой, проходящей через данную точку О2 с угловым коэффициентом 2/3, получим (х 2-3)=2/3(х 1-6), откуда 2 х 1-3 х 2=3.
Решая систему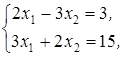 
находим координаты точки Е: х 1 = 51/13, х 2= 21/13, при этом L (E) = 1053/169.
Координаты точки Е можно найти следующим образом: дифференцируя выражение (x 1 — 6)2 + (х 2 — 3)2 как неявную функцию по x 1, получим 2(х 1-6)+2(х 2-3) 
=0,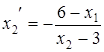 
.
Приравниваем полученное значение к тангенсу угла наклона прямой 3 x 1+2 x 2=15: 
или 2 x 1-3 x 2=3.
Решаем системууравнений 
получим координаты точки Е: х 1=51/13, х 2 = 21/13.
Ответ. Глобальный максимум, равный 52, находится в точке О(0,0). Глобальный минимум, равный 1053/169, находится в точке Е (51/13, 21/13).
Задача с нелинейной целевой функцией и нелинейной системой ограничений
Пример 38. Найти глобальные экстремумы функции
L =(х 1- 2)2 +(х 2 - 1)2
при ограничениях: х 12+ х 22≤16, х 1, х 2≥0.
Решение. Областью допустимых решений является окружность с радиусом 4, расположенная в первой четверти. Линиями уровня будут окружности с центром в точке О1(2,1). Глобальный минимум достигается в точке О 1. Глобальный максимум — в точке А(0,4), при этом
L (A)= (0 - 2)2 + (4 - I)2 = 4 + 9 = 13.
 |
 |
Рисунок 24
Ответ. Глобальный минимум, равный нулю, достигается в точке O1(2,1), глобальный максимум, равный 13, находится в точке А (0, 4).
Пример 39. Найти глобальные экстремумы L = х 12+ х 22 при ограничениях:
Решение. Область допустимых решений не является выпуклой и состоит из двух частей. Линиями уровня являются окружности с центром в точке О(0,0).
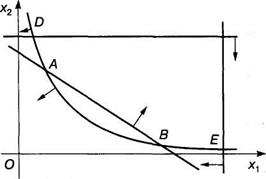
Рисунок 25
Найдем координаты точек А и В, решая систему
Получим А(1,4), В(4,1). В этих точках функция имеет глобальные минимумы, равные 17. Найдем координаты точек D и Е, решая системы
откуда получаем D(2/3,6) и L (D) = 328/9, Е (7,4/7) и L (E)= 2417/49.
|
|
|
Ответ. Целевая функция имеет два глобальных минимума, равных 17, в точках А(1,4) и В (4, 1), глобальный максимум, равный 2417/49, достигается в точке Е (7,4/7).
Метод множителей Лагранжа.
Постановка задачи
Дана задача нелинейного программирования L = f (x 1, х 2,..., хп) →max(min) при ограничениях:
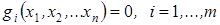. (51)
Предположим, что функции f (x 1, х 2,..., хп) и 
непрерывны вместе со своими первыми частными производными.
Ограничения заданы в виде уравнений, поэтому для решения задачи воспользуемся методом отыскания условного экстремума функции нескольких переменных.
Для решения задачи составляется функция Лагранжа
(52)
где λ i — множители Лагранжа.
Затем определяются частные производные:
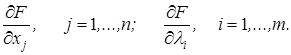
Приравняв к нулю частные производные, получим систему
(53)
Решая систему, получим множество точек, в которых целевая функция L может иметь экстремальные значения. Следует отметить, что условия рассмотренной системы являются необходимыми, но недостаточными. Поэтому не всякое полученное решение определяет точку экстремума целевой функции. Применение метода бывает оправданным, когда заранее предполагается существование глобального экстремума, совпадающего с единственным локальным максимумом или минимумом целевой функции.
Пример 40. Найти точку условного экстремума функции
L = х 1 х 2 + х 2 х 3
при ограничениях:
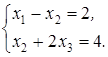
Решение. Составим функцию Лагранжа
.
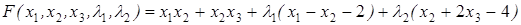Найдем частные производные функции Лагранжа по переменным х 1, х 2, х 3, λ1, λ2. Приравняв к нулю полученные выражения, решим систему
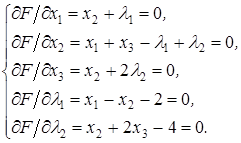
Откуда λ1= — х 2, λ2 = — х 2/2, х 1= —2, х 2 = —4, х 3 = 4, L = -8.
Определим характер экстремума, изменяя полученные значения переменных. Измененные значения должны удовлетворять заданной системе ограничений. Возьмем х 1> —2, например x 1=—1, тогда из системы ограничений получим х 2 = —3, х 3= 7/2, L = —15/2. Возьмем х 1 < —2, например х 1= —3, тогда получим х 2 = —5, х 3=9/2, L = —15/2. Следовательно, L = — 8 — минимальное значение функции.
Ответ. Точка экстремума х 1= —2, х 2 = —4, х 3 = 4, при этом минимальное значение функции L = — 8.
|
|
|
