 |
2. Механіка твердого тіла. 2.1. Обертальний рух твердого тіла. 2.1.1. Кінематика обертального руху матеріальної точки.. 2.1.2. Динаміка.
|
|
|
|
2. Механіка твердого тіла
Для проведення наступних лабораторних робіт необхідно розглянути теоретичні відомості з механіки твердого тіла.
2. 1. Обертальний рух твердого тіла.
Перш ніж розглядати величини i закони, які описують обертальний рух твердого тіла, проаналізуємо, як можна описати рух матеріальної точки уздовж кола радіуса r.
2. 1. 1. Кінематика обертального руху матеріальної точки.
Нехай в початковий момент часу матеріальна точка знаходилась в деякій точці А. За малий інтервал часу dt здійснюється мале переміщення ds уздовж дуги кола, при цьому радіус - вектор ОА повертається на кут dφ (рис. 1). При малих кутах повороту виконується співвідношення ds = r dφ , або у векторній формі
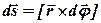(2. 1).
Вектором кутового переміщенняточки А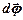 
називають вектор, довжина якого визначається значенням кута, на який повернувся радіус - вектор ОА, а напрямок визначається за правилом правого гвинта. Вектор 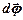знаходиться на осі обертання.
Рух точки характеризується вектором лінійної швидкості 
= 
, напрям якого збігається з напрямом переміщення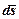 
, тобто він напрямлений уздовж дотичної до кола (дивіться Рис. 2. 1). Скористуємось співвідношенням (2. 1), продиференціюємо його за часом i одержимо вираз
(2. 2),
де 
- кутова швидкість.
Вектор кутової швидкості - це векторна величина, що дорівнює кутовому переміщенню, яке здійснюється в одиницю часу:
(2. 3)
Цей вектор, на відміну від лінійної швидкості, є аксіальним вектором.
Якщо швидкість матеріальної точки уздовж траєкторії змінюється, то в цьому випадку модуль тангенціального прискорення a =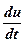 
, яке виникає за рахунок зміни модуля лінійної швидкості, відрізняється від нуля. В загальному випадку швидкість може змінюватись як за величиною, так і за напрямом. Складова прискорення, що визначається зміною швидкості за напрямом, має назву нормального прискорення. Цей вектор напрямлений перпендикулярно до швидкості і модуль його обчислюється за формулою
|
|
|
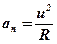(2. 4)
Модуль повного прискорення згідно з теоремою Піфагора дорівнює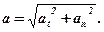 
Використовуючи визначення кутової швидкості i її зв`язок з лінійною швидкістю, одержимо
at =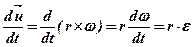 
(2. 5)
де ми ввели нову фізичну величину ε - кутове прискорення.
Вектор кутового прискорення - це векторна фізична величина, яка дорівнює зміні кутової швидкості, що відбувається за одиницю часу:
(2. 6)
Необхідно зауважити, що вектори кутової швидкості i кутового переміщення завжди збігаються за напрямами i напрямлені уздовж осі обертання (враховуючи правило правого гвинта). Напрям вектора кутового прискорення збігається з ними у випадку рівноприскореного руху i протилежний у випадку рiвносповільненого руху.
2. 1. 2. Динаміка.
Матеріальна точка А масою m, яка рухається зі швидкістю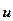 
, має імпульс 
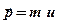в декартовій системі координат. Введемо в розгляд нову фізичну величину - момент імпульсу. Її можна визначити відносно точки та відносно осі. Під моментом імпульсу 
матеріальної точки відносно довільної точки О розуміють векторний добуток радіус - вектора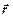 
точки А та імпульсу 
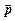точки А:
(2. 7)
Цей вектор напрямлений перпендикулярно до площини, в якій лежать вектори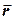 
і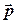 
(дивіться Рис. 2. 2) відповідно до правила правого гвинта. Модуль вектора 
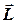обчислюється як 
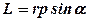, де α - кут між напрямами 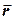і 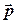. Якщо точка А рухається по колу, то швидкість напрямлена уздовж дотичної, тобто перпендикулярна до радіус - вектора 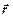, тому кут α = 90о. В цьому випадку вираз для модуля моменту імпульсу дещо спрощується:
|
|
|
(2. 8)
Момент імпульсу може бути визначений також відносно довільної осі z (рис. 2. 3). Візьмемо площину, перпендикулярну до осі z, яка проходить через точку А. Проведемо в цій площині від осі до точки А радіус - вектор 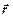. Розкладемо імпульс 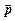точки А на дві складові: 
, напрямлену уздовж осі z, i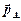 
, яка лежить в площині. Моментом імпульсу 
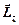точки А відносно осі z будемо називати векторний добуток радіуса - вектора 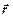та складової 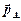імпульсу цієї точки, тобто
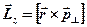(2. 9)
Якщо матеріальна точка рухається по колу радіуса r, то складова моменту імпульсу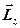 
напрямлена перпендикулярно радіус - вектору i тому кут α , який визначає модуль векторного добутку, прямий. Саме тому величина моменту імпульсу визначається так:
(2. 10)
Порівнюючи співвідношення (2. 7) та (2. 9), ми можемо зробити висновок: моменти імпульсу відносно довільної точки О i відносно осі z, яка проходить через цю точку, збігаються лише у випадку руху матеріальної точки А по колу в площині, перпендикулярній до осі z.
Враховуючи зв`язок між лінійною та кутовою швидкостями обертової точки u = ω r, вираз (2. 10) можна перетворити до вигляду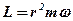 
i ввести в розгляд нову динамічну характеристику матеріальної точки - момент інерції.
Момент інерції матеріальної точки характеризує інертність матеріальної точки по відношенню до обертального руху i визначається як добуток маси матеріальної точки на квадрат відстані до осі обертання
Урахуємо, що вектори кутової швидкості та моменту імпульсу однаково спрямовані. Тоді ми можемо записати:
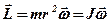(2. 11)
тобто момент імпульсу дорівнює добутку моменту інерції i кутової швидкості обертального руху. У загальному випадку при русі матеріальної точки змінюються r i u. Звідси буде змінюватись також L. Знайдемо похідну вектора 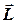по часу:
|
|
|
(2. 12)
Згадаємо, що 
, 
(другий закон Ньютона), а також врахуємо паралельність векторів швидкості та імпульсу. Тоді можемо одержати:
(2. 13)
де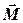 
- момент сили, який можна ввести по аналогії з моментом імпульсу.
Нехай сила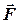 
прикладена до матеріальної точки А. Під моментом сили відносно точки О розуміють векторний добуток радіус - вектора r, проведеного від точки О до точки А, i вектора сили 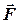, тобто
(2. 14)
Цей вектор перпендикулярний до площини, в якій лежать у вiдповiдностi до правила правого гвинта. Його абсолютна величина визначається, як
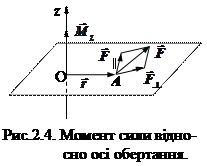M = rFsinα ,
де α - кут між 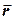і 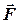(рис. 2. 4).
Нехай у просторі існує вісь z, відносно якої ми будемо обчислювати момент сили Mz (рис. 2. 4). Моментом сили Mz відносно осі Z будемо називати векторним добутком радіуса - вектора 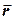i складової 
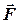сили , тобто
(2. 14а)
Як можна побачити, моменти сил відносно точки та відносно осі, яка проходить через цю точку, дорівнюють один одному тільки тоді, коли сила діє уздовж дотичної до кола з центром в точці О, що лежить в площині, перпендикулярній до осі. Рівняння (2. 13), що ми отримали раніш, є аналогом другого закону Ньютона i тому воно є основним рівнянням динаміки обертального руху.
Швидкість зміни моменту імпульсу матеріальної точки дорівнює векторній сумі моментів сил, які прикладені до точки:
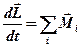(2. 15)
Це рівняння можна записати також i інакше. Зробимо підстановку в це рівняння виразу (2. 11), далі продиференціюємо по часу i врахуємо також співвідношення (2. 6). Тоді ми одержимо:
(2. 16)
Таким чином, векторна сума моментів усіх сил, діючих на матеріальну точку, дорівнює добутку його моменту інерції та кутового прискорення
|
|
|
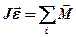(2. 17)
При русі матеріальної точки масою m по колу радіуса r зі швидкістю u вона має кінетичну енергію 
. Урахуємо, що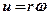 
. Тоді
(2. 18)
тобто кінетична енергія точки, яка рухається по колу, дорівнює половині добутку його моменту інерції на квадрат кутової швидкості.
Розглянемо тепер обертальний рух абсолютно твердого тіла .
Абсолютно твердим тілом будемо називати тіло, відстань між будь-якими двома точками якого не змінюється при будь - яких його переміщеннях. При обертальному русі усі точки тіла рухаються по колам, центри яких лежать на одній прямій лінії - осі обертання, а площини яких перпендикулярні цій осі (рис. 2. 6). При обертанні радіус, проведений від осі перпендикулярно їй до довільної точки А цього тіла, повернеться на кут dφ за час dt. Внаслідок постійності взаємного розташування точок тіла на такий самий кут повернуться будь-які інші радіуси. Саме тому цей кут можна вважати величиною, яка буде характеризувати обертальний рух всього твердого тіла. Далі можна говорити про кутову швидкість та кутове прискорення
твердого тіла:
i 
Якщо є система матеріальних точок, то момент інерції цієї системи відносно деякої осі обертання дорівнює сумі моментів інерції окремих матеріальних точок відносно цієї ж самої осі:
(2. 19)
Ця властивість моменту інерції, так само як і маси тіла, має назву адитивності.
Перейдемо тепер до твердого тіла. Розбиваємо уявно тіло на нескінченну кількість елементів з нескінченно малими розмірами масами dm кожний. Момент інерції кожного елемента dmr2, інтегруємо по всім елементам, знаходимо момент інерції твердого тіла:
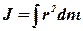(2. 19а)
В багатьох випадках доводиться розглядати момент інерції твердого тіла відносно різних осей. В цьому випадку можна використовувати теорему Штейнера. Нехай момент інерції твердого тіла масою m відносно осі, яка проходить через центр мас тіла, дорівнює Jо. Тоді момент інерції цього тiла J відносно осі, паралельної першій i розташованої на відстані d від неї, можна обчислити за формулою:
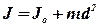(2. 20)
Зроблені зауваження дозволяють узагальнити усі характеристики, які ми раніше ввели для матеріальної точки, на випадок обертального руху твердого тіла. Це такі характеристики, як момент імпульсу, момент сили, кінетична енергія та інші. Крім того, можна також використовувати основне рівняння динаміки обертального руху у вигляді (2. 13а) або (2. 17).
|
|
|
На закінчення зазначимо, що формально рівняння поступального i обертального руху переходять одне в одне, якщо зробити одночасну заміну усіх характеристик, які описують поступальний рух, на відповідні характеристики обертального руху:
· переміщення ds - кутове переміщення dφ
· швидкість u - кутова швидкість ω
· прискорення а - кутове прискорення ε
· маса m - момент інерції J
· сила F - момент сили M
· імпульс p - момент імпульсу L
|
|
|
