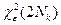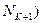 |
2 Планирование эксперимента
|
|
|
|
При планировании эксперимента определяют необходимое количество объектов в экспериментальной группе для обеспечения представительности выборки из генеральной совокупности АТС. Пусть целью эксперимента является оценка показателей надежности А с вероятностью а, которая втеории вероятности и математической статистике называется двусторонней доверительной вероятностью. Это означает, что оцениваемый показатель надежности А должен находиться в интервале [Aн ; 
Aв], где Aни Aв- нижняя и верхняя доверительные границы.
Если задать Aн = 0, то получим нижний односторонний интервал, а если Aв = ∞, то получим верхний односторонний интервал. В этих случаях необходимо задавать экспериментатору одностороннюю доверительную вероятность у. Чем больше а (или у), тем больше должен быть объем выборки, и соответственно увеличатся затраты на проведение эксперимента. При этих условиях следует принимать решения к точности оценки показателей надежности с учетом стратегии процесса замены конкретного элемента АТС. Согласно ГОСТ 27. 502 83 для плана испытаний [NUN] по закону Вейбулла-Гнеденко минимальный объем выборки определяется по уравнению:
, (1)
где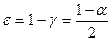 
- уровень значимости, т. е. вероятность выхода оцениваемого параметра за одностороннюю доверительную границу;
b – параметр формы закона Вейбулла-Гнеденко, принимается в зависимости от коэффициента вариации V;
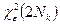- квантиль распределения с 
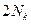степенями свободы, соответствующая уровню значимости 
;
- предельная относительная ошибка оценки соответствующего показателя надежности А, которая определяется как
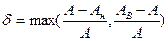; (2)
|
|
|
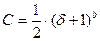- постоянная при заданных значениях и b.
Минимальный объем выборки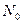 
можно рассчитывать по следующему алгоритму:
1. На первом этапе целесообразно определить исходные данные для расчета: предполагаемый коэффициент вариации технического ресурса (наработки до отказа), рассматриваемого элемента АТС – V(L); - предельную относительную ошибку оцениваемого параметра надежност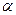и; 
(или 
) – доверительную вероятность оценки.
Предварительно определяют уровень значимости 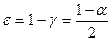. По табл. 1 необходимо определить параметр формы b закона Вейбулла-Гнеденко, определяющий характер изменения теоретической кривой. Затем определяем константу С по формуле:
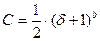(3)
2. Далее определить первое и второе приближения к максимальному объему выборки по формулам:
(4)
(5)
Присвоив индексу k начальное значение 1, приступить к решению уравнения (1) итерацией методом секущей.
3. Начало цикла итерации. Определить f( 
) и f( 
) по формуле (1). Значение 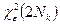брать из табл. 3 в зависимости от и m=2N0. Рассчитать следующее приближение минимального объема выборки по формуле:
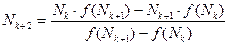(6)
Дополнить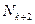 
до ближайшего большего целого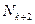 
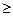
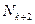. Если = 
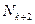итерация завершена, то переходим к п. 4 данного алгоритма.
4. Минимальный объем выборки при заданных значениях V, , 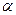(или ) равен = .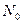
Рассмотрим пример расчета объема выборки - 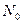. Пусть требуется оценить с двусторонней доверительной вероятностью 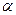=0, 90 среднюю наработку до отказа рулевого механизма. Воспользовавшись результатами предыдущих испытаний, зададим значения коэффициента вариации V= 0, 30 и предельную относительную ошибку =0, 09.
Уровень значимости равен 
.
Из табл. 1 приложение 1 выбираем b =3, 7138. Константа
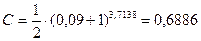
Определяем первое приближение
|
|
|
(3, 36),
затем второе приближение
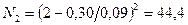(1, 778)
Округляя полученное значение до целого числа, получим 
=44.
Для наглядности результаты промежуточных расчетов представлены в табл. 1.
Таблица 1 - Определение минимального объема выборки методом итерации
| k |
|
|
|
| f( | f( |
|
|
| 34, 764 | 67, 373 | -1, 062 | 2, 393 | 30, 840 | ||||
| 67, 373 | 44, 889 | 2, 393 | -0, 089 | 31, 466 | ||||
| 44, 889 | 46, 595 | -0, 089 | 0, 085 | 31, 511 |
На этом процесс итерации заканчивается.
Итак, чтобы оценить среднюю наработку до отказа рулевого механизма с двусторонней доверительной вероятностью 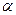=0, 90 и предельной относительной ошибки =0, 09, необходимо включить в эксперимент не менее N0 = 32 автомобилей.
Далее по экспериментальным данным, полученным в реальных условиях эксплуатации ТС, составляют вариационные (упорядоченные в порядке возрастания значений) ряды наработок между отказами элементов автомобиля. Для каждого ряда рассчитывают выборочные характеристики, с помощью которых можно оценивать количественные показатели надежности.
|
|
|
