 |
Таблица 3.2 - Таблица истинности формулы
|
|
|
|
Таблица 3. 2 - Таблица истинности формулы
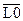 i=kj× Lед i=kj× Lед
| SiÎ Sj | Итого | |
Используя формулу (3. 14), формируем семейство подмножеств {Sj|j=1, 2,., Z} шифров элементов, вошедших в ступени профилактики. Они вместе с множеством 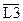 представляют номенклатуру и периодичность ступеней профилактики, которые, путем наложения друг на друга при совпадении в момент наработки L x, образуют РТВ.
представляют номенклатуру и периодичность ступеней профилактики, которые, путем наложения друг на друга при совпадении в момент наработки L x, образуют РТВ.
Формирование разновидностей технических воздействий за интервалом периодического восстановления осуществляется по следующему алгоритму. Напомним, что интервал периодического восстановления -интервал наработки автомобиля от одного совпадения всех ступеней профилактики до следующего их совпадения. Длина Lипв определяется как наименьшее общее кратное (НОК) множество значений периодичности ступени профилактики -центра группирования периодичности замен элементов 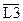 :
:
Lипв = НОК{  |j=1, 2,., Z} (3. 15)
|j=1, 2,., Z} (3. 15)
Из формулы (3. 15) ясно, что множеству значений периодичности ступеней профилактики 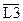 соответствует и множество значений кратности в виде расчетных коэффициентов Кпр={k1,., k Z}.
соответствует и множество значений кратности в виде расчетных коэффициентов Кпр={k1,., k Z}.
Коэффициент кратности – есть отношение множество значений периодичности ступеней профилактики к длине единичного интервала.
Тогда кратность Lипв можно выразить через коэффициенты кратности:
Kипв = НОК{kj|j=1, 2,., Z} (3. 16)
Например, если Lед = 41. 15 тыс. км., а Lсс = 0, 195 тыс. км, тогда множество L3 состоит из элементов {41. 15 тыс. км.; 82. 29 тыс. км.; 123, 44 тыс. км. }.
При этом кратность интервала периодичности Kипв состоит из элементов {1, 2, 3, 4} или Kипв =12 единичных интервалов. Интервал периодического восстановления составит Lипв = 490 тыс. км, а объект достигнет предельного состояния. Для примера на рис. 3. 6 представлен механизм формирования РТВ из ступеней профилактики.
|
|
|

Рисунок 3. 6 - Механизм формирования разновидностей технических воздействий
Формирование номенклатуры элементов в РТВ и расчет их потребности предлагается по следующему алгоритму.
Формируем матрицу-строку A, элементы которой определим по формуле:
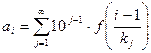 , где: i=1, 2,., КИПВ (3. 17)
, где: i=1, 2,., КИПВ (3. 17)
где:  - булева функция, которая принимает значение 1 (истина) при
- булева функция, которая принимает значение 1 (истина) при 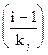 целому числу. В другом случае, при
целому числу. В другом случае, при 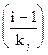 =0, принимает значение 0 (ложь). Элемент a1 является максимальным элементом матрицы-строки A. Известно, если элемент a1 является двоичным числом, тогда все разряды равны единице.
=0, принимает значение 0 (ложь). Элемент a1 является максимальным элементом матрицы-строки A. Известно, если элемент a1 является двоичным числом, тогда все разряды равны единице.
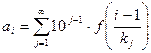
 (3. 18)
(3. 18)
В десятичной системе счисления a1 соответствует числу 2Z-1. Из комбинаторики известно, что это есть количество всех возможных сочетаний из Z элементов:
 (3. 19)
(3. 19)
Из этого следует, что элементы матрицы-сроки A не могут быть больше 2Z-1.
Формируем матрицу-строку B, элементы которой определим по следующей пропозициональной формуле:

 (3. 20)
(3. 20)
где: i=1, 2, …, KИПВ;
(m)2. - число m =1, 2,., 2 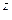 - 1 в двоичной системе счисления;
- 1 в двоичной системе счисления;
j- номер РТВ, начальное значение равно j0=1.
Увеличиваем на единицу при выполнении присваивания bj=ai и определяем следующий элемент матрицы-строки B. В результате получим матрицу-строку B с количеством элементов n £ 2Z-1, равным количеству РТВ.
Каждый разряд двоичных чисел bj{j=1, 2,..., n} указывает на наличие (1) или отсутствие (0) соответствующей ступени профилактики, в составе данной РТВ.
Для рассматриваемого примера, применяя формулы (3. 20) и (3. 21), получим следующие матрицы-строки:
A = || 111, 1, 11, 101, 1101, 1, 111, 1, 1101, 101, 11, 1 ||
|
|
|
и
B = || 1, 11, 101, 111, 1101, 1111 ||
Таблица 3. 3 - Таблица истинности формулы (3. 20) при j=2
| ai=(m)2 | ai=br | bj=ai | Итого |
Пусть {Rj|j=1, 2,., n} семейство подмножеств множества R шифров элементов автомобиля, составляющих номенклатуру РТВ. Каждый из них формируется из подмножеств семейства {Sr|r=1, 2,., n} по формуле:
 , j=1, 2,., n (3. 21)
, j=1, 2,., n (3. 21)
где: Sr -подмножество шифров элементов автомобиля, входящих в r-ю ступень профилактики;
f(bjr)-булева функция, принимающая значение r-го разряда двоичного числа bj (т. е. элемента матрицы-строки B).
Для уточнения затрат при формировании необходимо учесть, что в одну РТВ могут попасть элементы, являющиеся составными частями других элементов, например, деталь может входить в узел, а узел в агрегат. Действительную номенклатуру элементов РТВ предлагается определять следующим способом (на примере одного подмножества Rj).
Упорядочиваем элементы подмножества Rj в порядке возрастания значений, например, считая шифры десятичными числами. Представим Rj в виде матрицы:

Матрица, условно может быть разделена на несколько фрагментов. В пределах каждого из них Na= const. При этом во фрагмент с Na=0 объединены шифры узлов и деталей, не входящих в состав какого-либо агрегата. В свою очередь, каждый фрагмент может состоять из подфрагментов по количеству узлов в агрегате. В пределах каждого из них Nо=const. Начинаем поиск шифра агрегата или узла с первого столбца матрицы Rj анализом на нуль элементов второй и третьей строки. Если Nо< > 0 и Nа=0, то найден шифр узла и весь под фрагмент должен быть заменен найденным шифром узла. Если Nо=0 и Nа=0, то найден шифр агрегата. Тогда весь фрагмент заменяется найденным шифром агрегата. В итоге получим семейство подмножеств {  |j=1, 2,., n} множества
|j=1, 2,., n} множества  шифров элементов, представляющих действительную номенклатуру элементов, входящих в РТВ.
шифров элементов, представляющих действительную номенклатуру элементов, входящих в РТВ.
|
|
|


