Расчетные формулы  для определения параметров  

Расчетные   формулы  для   определения   параметров     

             поступательного движения тела

Все точки тела движутся одинаково.

Закон равномерного движения: S = So + vt.

Закон равнопеременного движения:

Здесь So— путь, пройденный до начала отсчета, м;

 v o —начальная скорость движения, м/с;

at — постоянное касательное ускорение, м/с²

Скорость: v = S´; v = vo + att.

Ускорение: at = v´.

Закон неравномерного движения: S = f(t³).

Кинематические графики поступательного движения предста­влены на рис. П4. 1.

              

 

                  Практическое занятие 4                                             153

              Расчетные формулы для   определения параметров

                                    вращательного   движения

 

Точки тела движутся по окружностям вокруг неподвижной оси (оси вращения).

Закон равномерного вращательного движения: φ = φ o+ ω t.

Закон равнопеременного вращательного движения:

Законнеравномерного вращательного движения: φ = f(t³).

Здесь φ — угол поворота тела за время t, рад;

ω — угловая скорость, рад/с;

φ o— угол поворота, на который развернулось тело до начала отсчета;

ω о — начальная угловая скорость;

ε — угловое ускорение, рад/с²;

Угловая скорость: ω = φ '; ω = ω o + ε t;

Угловое ускорение: ε = ω '.

Кинематические графики вращательного движения представле­ны на рис. П4. 2.

                 

Число оборотов вращения тела: z = φ /(2π ).

 Угловая частота вращения: n, об/мин.

             

154                                            Практическое занятие 4

   Рекомендации для решения задач  

         расчетно-графической  работы

Задание 1

1. Определить вид движения на каждом участке по приведенно­му кинематическому графику.

2. Записать законы движения шкива на каждом участке. Параметры движения в конце каждого участка являются начальными параметрами движения на каждом последующем.

3. Определить полный угол поворота шкива за время вращения. Использовать формулу для перехода от угловой частоты вращения к угловому ускорению.

4. Определить полное число оборотов шкива, используя формулу

                                                      

5. Построить графики угловых перемещений и угловых
ускорений.

6. Определить нормальное и касательное ускорения точки на
ободе шкива в указанные моменты времени.

Задание 2

1. Подставив заданные коэффициенты в общее уравнение движения, определить вид движения.

2. Определить уравнение скорости и ускорения груза.

Расчетно-графическая  работа

Задание 1. Частота вращения шкива диаметром d меняется со­гласно графику. Определить полное число оборотов шкива за время движения и среднюю угловую скорость за это же время. Построить

        Практическое занятие 4                                            155

график угловых перемещений и угловых ускорений шкива. Опреде­лить ускорения точек обода колеса в моменты времени t1 и t2.

 

 

  

 

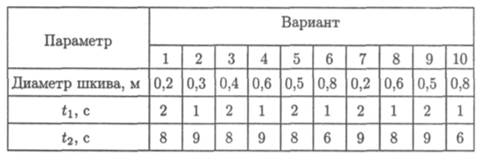
   Задание 2. Движение груза А задано уравнением

 у = at² + bt + с, где [у] = м, [t] = с. Определить скорость и ускорение груза в моменты времени t1 и t2, а также скорость и ускорение точки В на ободе барабана лебедки (рис. П4. 4).

156                                     Практическое занятие 4

 

При защите работы ответить на вопросы тестового задания.

        Тема 1. 9. Кинематика.

 Простейшие движения твердого тела

                    Практическое занятие 4                                           157

 

158                                        Практическое занятие 5

Практическое занятие 5

Темы 1. 14, 1. 15. Работа и мощность.

Общие теоремы динамики

Знать зависимости для определения мощности при поступа­тельном и вращательном движениях. КПД.

Знать основные уравнения динамики при поступательном и вращательном движениях твердого тела.

Уметь рассчитывать мощность с учетом потерь на трение и сил инерции.

Уметь определять параметры движения с помощью теорем динамики.

⇐ Предыдущая26272829303132333435Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: