 |
Расчетные формулы. Пример 1. Определение равнодействующей системы сил. Решение. Расчетно-графическая работа 1. Определение равнодействующей плоской системы сходящихся сил аналитическим и геометрическим способами
|
|
|
|
Расчетные формулы
Равнодействующая системы сил

где F∑ x, F∑ y — проекции равнодействующей на оси координат;
Fkx, Fky —проекции векторов-сил системы на оси координат.

где α ∑ х — угол равнодействующей с осью Ох.
Условие равновесия 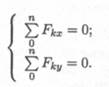
Если плоская система сходящихся сил находится в равновесии, многоугольник сил должен быть замкнут.
Пример 1. Определение равнодействующей системы сил
Определить равнодействующую плоской системы сходящихся сил аналитическим и геометрическим способами (рис. П1. 1). Дано:
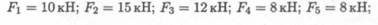
Практическое занятие 1 131
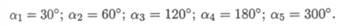
Решение
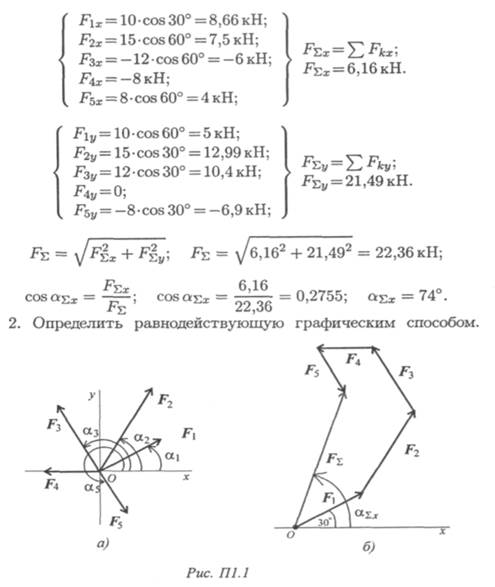
1. Определить равнодействующую аналитическим способом (рис. П1. 1а).
132 Практическое занятие 1
С помощью транспортира в масштабе 2 мм = 1 кН строим многоугольник сил (рис. П1. 16). Измерением определяем модуль равнодействующей силы и угол наклона ее к оси Ох.

Результаты расчетов не должны отличаться более чем на5 %:
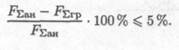
Расчетно-графическая работа 1
Определение равнодействующей плоской системы сходящихся сил аналитическим и геометрическим способами
Задание. Используя схему рис. П1. 1а, определить равнодействующую системы сил.

Практическое занятие 1 133
Пример 2. Решение задачи на равновесие аналитическим способом
Грузы подвешены на стержнях и канатах и находятся в равновесии. Определить реакции стержней АВ и СВ (рис. П1. 2).
|
|
|
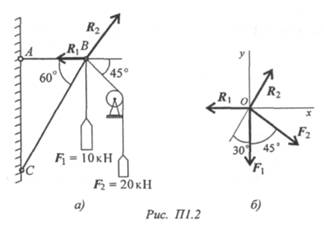
Решение
1. Определяем вероятные направления реакций (рис. П1. 2а). Мысленно убираем стержень АВ, при этом стержень С В опускается, следовательно, точка В отодвигается от стены: назначение стержня АВ — тянуть точку В к стене.
Если убрать стержень СВ, точка В опустится, следовательно, стержень СВ поддерживает точку В снизу — реакция направлена вверх.
2. Освобождаем точку В от связи (рис. П1. 26).
3. Выберем направление осей координат, ось Ох совпадает с реакцией R 1.
4. Запишем уравнения равновесия точки В:
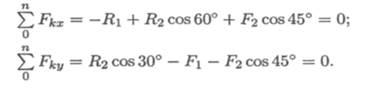
134 Практическое занятие 1
5. Из второго уравнения получаем:

Вывод: стержень АВ растянут силой 28, 07 кН, стержень СВ сжат силой 27, 87 кН.
Примечание. Если при решении реакция связи окажется отрицательной, значит, вектор силы направлен в противоположную сторону.
В данном случае реакции направлены, верно.
Расчетно-графическая работа 2
Условие равновесия плоской системы сходящихся сил в аналитической форме
Задание. Определить реакции стержней АС иAD (рис. П1. 3).

При защите работ ответить на вопросы карт с тестовыми заданиями.
Практическое занятие 1 135
Темы 1. 1, 1. 2. Статика.
Плоская сходящаяся система сил

136 Практическое занятие 1

 Практическое занятие 2 137
Практическое занятие 2 137
Практическое занятие 2
Тема 1. 4. Плоская система произвольно
расположенных сил
Знать теорему Пуансо о приведении силы к точке.
Уметь приводить произвольную плоскую систему сил к точке, определяя величины главного вектора и главного момента системы.
|
|
|
Знать три формы уравнений равновесия и уметь ими пользоваться при определении реакций в опорах балочных систем.
Основные формулы и предпосылки расчета

138 Практическое занятие 2
Главный момент
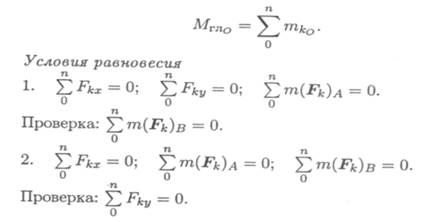
Упражнения при подготовке к самостоятельной
работе
1. Перенести силу F в точку А, используя теорему Пуансон (рис. П2. 3). F = 20 кН; АВ = 6 м; ВС = 2 м.

2. Привести систему сил к точке В, определить главный вектор
и главный момент системы сил (рис. П2. 4). АВ = 2 м; ВС = 1, 5 м;
CD = 1м. F1 = 18 кН; F2 = 10 кН; F3 = 30 кН; т = 36кН∙ м.

Практическое занятие 2 139
3. Система сил находится в равновесии. Определить величину
момента пары т (рис. П2. 5). F1 = F'1 = 10кН; F2 = F'2 = 20 кН.

4. Нанести реакции в опорах балок 1 и 2 (рис. П2. 6).

5. Определить величину реакции в опоре А. Приложена распределенная нагрузка интенсивностью q = 5кН/м (рис. П2. 7).

6. Записать систему уравнений равновесия для определения реакций в опоре защемленной балки.
7. Записать систему уравнений равновесия для определения реакций в опорах двухопорной балки, закрепленной на двух шарнирах.
140 Практическое занятие 2
|
|
|


