 |
Решение. Контрольные вопросы и задания. Тема 1.14. Динамика. Работа и мощность. Тема 1.15. Общие теоремы динамики
|
|
|
|
Решение
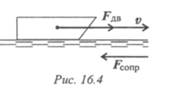 1. Определяем полезную мощность, используемую на движение с заданной скоростью:
1. Определяем полезную мощность, используемую на движение с заданной скоростью: 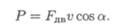
118 Лекция 16

2. По формуле для полезной мощности можно определить движущую силу судна с учетом условия α = 0. При равномерном движении движущая сила равна силе сопротивления воды: Fдв = Fconp.
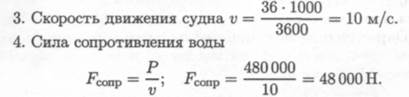
Сила сопротивления воды движению судна Fсопр = 48 кН.
Пример 3. Точильный камень прижимается к обрабатываемой детали с силой 1, 5 кН (рис. 16. 5). Какая мощность затрачивается на обработку детали, если коэффициент трения материала камня о деталь 0, 28; деталь вращается со скоростью 100 об/мин, диаметр детали 60 мм.
 Решение
Решение
1. Резание осуществляется за счет трения между точильным камнем и обрабатываемой деталью:

3. Угловая скорость вращения детали

4. Мощность, необходимая для обработки детали:

Контрольные вопросы и задания
1. Запишите формулы для расчета работы при поступательном и вращательном движениях.
Тема 1. 14. Работа и мощность. КПД 119
2. Вагон массой 1000 кг перемещают по горизонтальному пути
на 5 м, коэффициент трения 0, 15. Определите работу силы тяжести.
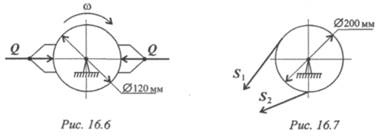
3. Колодочным тормозом останавливают барабан после отключения двигателя (рис. 16. 6). Определите работу торможения за 3 оборота, если сила прижатия колодок к барабану 1 кН, коэффициент трения 0, 3.
4. Натяжение ветвей ременной передачи S1 = 700 Н, S2 = 300 Н
(рис. 16. 7). Определите вращающий момент передачи.
5. Запишите формулы для расчета мощности при поступательном и вращательном движениях.
|
|
|
6. Определите мощность, необходимую для подъема груза весом 0, 5 кН на высоту 10 м за 1 мин.
7. Определите общий КПД механизма, если при мощности двигателя 12, 5 кВт и общей силе сопротивления движению 2 кН скорость движения 5 м/с.
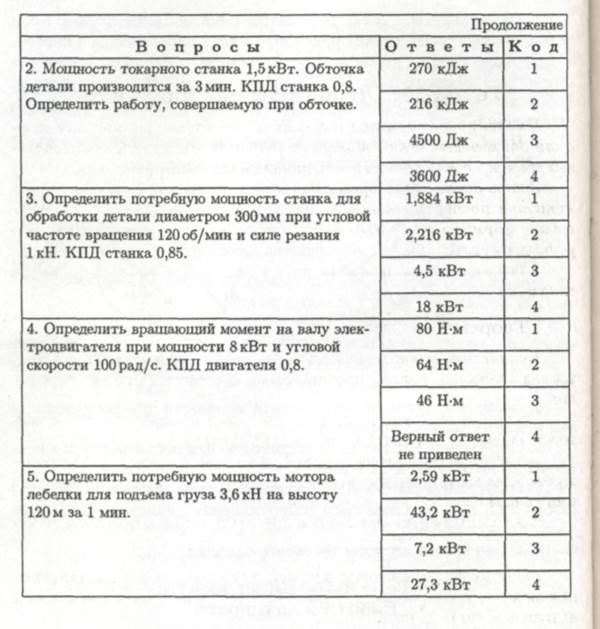
8. Ответьте на вопросы тестового задания.
Тема 1. 14. Динамика.
Работа и мощность

120 Лекция 16
Тема 1. 15. Общие теоремы динамики 121
ЛЕКЦИЯ 17
Тема 1. 15. Общие теоремы динамики
Иметь представление о понятиях «импульс силы», «количество движения», «кинетическая энергия»; о системе материальных точек, о внутренних и внешних силах системы.
Знать основные теоремы динамики, основные уравнения динамики при поступательном и вращательном движениях твердого тела, формулы для расчета моментов инерции некоторых однородных твердых тел.
Уметь определять параметры движения с помощью теорем динамики.
Теорема об изменении количества движения
Количеством движения материальной точки называется векторная величина, равная произведению массы точки на ее скорость mv.
Вектор количества движения совпадает по направлению с вектором скорости. Единица измерения [mv] — кг∙ м/с.
Произведение постоянного вектора силы на некоторый промежуток времени, в течение которого действует эта сила, называется импульсом силы Ft.
Вектор импульса силы по направлению совпадает с вектором силы.

Использовав основное уравнение динамики, после преобразования можно получить соотношение между количеством движения и импульсом силы (рис. 17. 1).

122 Лекция 17
|
|
|
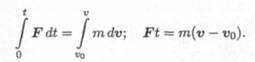
Полученное соотношение выражает теорему об изменении количества движения точки:
Изменение количества движения точки за некоторый промежуток времени равно импульсу силы, действующему на точку в течение того же промежутка времени.
Теорема об изменении кинетической энергии
Энергией называется способность тела совершать механическую работу.
Существуют две формы механической энергии: потенциальная энергия, или энергия положения, и кинетическая энергия, или энергия движения.
Потенциальная энергия (П) определяет способность тела совершать работу при опускании с некоторой высоты до уровня моря. Потенциальная энергия численно равна работе силы тяжести.
П = Gh, где h — высота точки над уровнем моря.
Кинетическая энергия (К) определяется способностью движущегося тела совершать работу. Для материальной точки кинетическая энергия рассчитывается по формуле 
Кинетическая энергия — величина скалярная, положительная.
Единицы измерения:
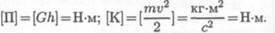
Энергия имеет размерность работы.
Запишем для материальной точки (рис. 17. 2) основное уравнение движения
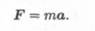
 Спроектируем обе части векторного равенства на направление скорости:
Спроектируем обе части векторного равенства на направление скорости:

Тема 1. 15. Общие теоремы динамики 123
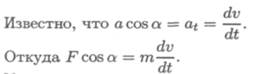
Умножив обе части полученного выражения на некоторое перемещение dS, получим:

Полученное равенство выражает теорему об изменении кинетической энергии точки:
Изменение кинетической энергии на некотором пути равно работе всех действующих на точку сил на том же пути.
|
|
|


