Тема 2.3. Практические расчеты на срез и смятие

     Тема 2. 3. Практические расчеты на срез и смятие

 

                  Тема 2. 3. Практические расчеты на срез и смятие                    207

 

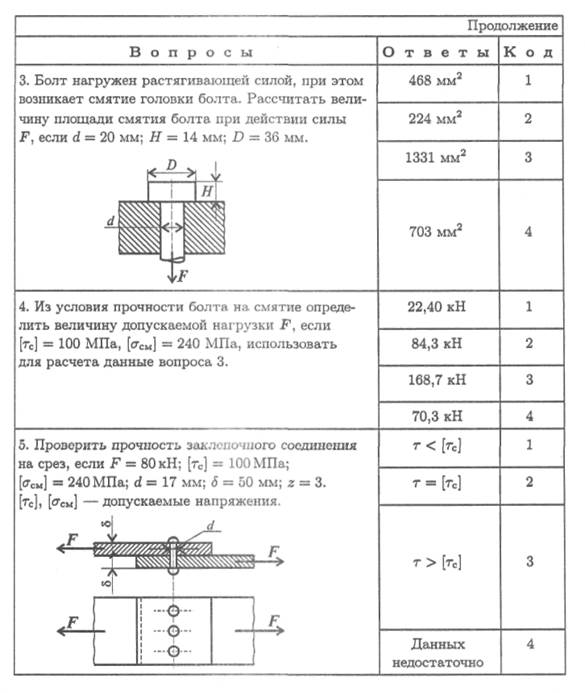
208                                                                                   Лекция 25

ЛЕКЦИЯ 25

Тема 2. 4. Геометрические характеристики плоских сечений

Иметь представление о физическом смысле и порядке опре­деления осевых, центробежных и полярных моментов инерции, о главных центральных осях и главных центральных моментах инерции.

Знать формулы моментов инерции простейших сечений, спо­собы вычисления моментов инерции при параллельном переносе осей.

При растяжении, сжатии, смятии и сдвиге деталь сопротивля­ется деформации всем сечением одинаково. Здесь геометрической ха­рактеристикой сечения является площадь.

При кручении и изгибе сечение сопротивляется деформации не одинаково, при расчетах напряжений появляются другие геометри­ческие характеристики сечения, влияющие на сопротивления сече­ния деформированию.

Статический момент площади сечения

Рассмотрим произвольное сечение (рис. 25. 1).

                                              

Если разбить сечение на бесконечно малые площадки dA и умножить каждую площадку на расстояние до оси координат и проинтегрировать полученное выраже­ние, получим статический момент площади сечения:

Для симметричного сечения статические моменты каждой по­ловины площади равны по величине и имеют разный знак. Следова­тельно, статический момент относительно оси симметрии равен нулю.

Статический момент используется при определении положения

               Тема 2. 4. Геометрические характеристики плоских сечений                   209

центра тяжести сечения:

               

Формулы для определения положения центра тяжести можно за­писать в виде 

                                       

         Центробежный момент инерции

Центробежным моментом инерции сечения называется взятая по всей площади сумма произведений элементарных площадок на обе координаты:       

                                             

Центробежный момент инерции может быть положительным, отрицательным и равным нулю. Центробежный момент инерции от­носительно осей, проходящих через центр тяжести сечения, равен нулю.

Оси, относительно которых центробежный момент равен нулю, называются главными. Главные оси, проходящие через центр тяже­сти, называют главными центральными осями сечения.

         Осевые   моменты инерции

Осевым моментом инерции сечения относительно некоторой оси, лежащей в этой же плоскости, называется взятая по всей пло­щади сумма произведений элементарных площадок на квадрат их расстояния до этой оси:

1) осевой момент инерции сечения относительно оси Ох

210                                                                                    Лекция 25

        Полярный момент инерции сечения

Полярным моментом инерции сечения относительно некоторой точки (полюса) называется взятая по всей площади сумма произве­дений элементарных площадок на квадрат их расстояния до этой точки:

где р — расстояние до полюса (центра поворота) (рис. 25. 1).

Поскольку р ² = х² + у², получим: полярный момент инерции сечения равен сумме осевых: Осевые моменты инерции характеризуют сопротивление сече­ния повороту относительно соответствующей оси.

Полярный момент инерция характеризует сопротивление сече­ния повороту вокруг полюса (начала координат). Единицы измере­ния моментов инерции: м⁴; см⁴; мм⁴.

        Моменты инерции простейших сечений

Осевые моменты инерции прямоугольника (рис. 25. 2)

                                         

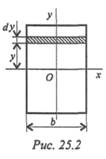
Представим прямоугольник высотой h и ши­риной bв виде сечения, составленного из бесконеч­но тонких полос. Запишем площадь такой полосы: bdy = dA. Подставим в формулу осевого момента  инерции относительно оси Ох:          

                      

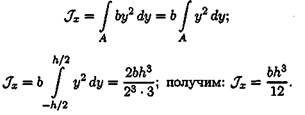
По аналогии, если разбить прямоугольник на вертикальные по­лосы, рассчитать площади полос и подставить в формулу для осе­вого момента инерции относительно оси Оу, получим:

                                     Тема 2. 4. Геометрические характеристики плоских сечений                               211

                 

Очевидно, что при h > b сопротивление повороту относительно оси Ох больше, чем относительно Оу.

Для квадрата:

⇐ Предыдущая39404142434445464748Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: