Примеры решения задач. Решение.   Контрольные  вопросы и задания. Тема 2.5. Кручение. Напряжения и деформации. при кручении

      Примеры решения задач

Пример 1. На распределительном валу (рис. 26. 3) установлены четыре шкива,  на   вал   через   шкив   1  подается  мощность  12 кВт,  кото­рая  через шкивы 2, 3, 4  передается  потребителю;  мощности распре­деляются   следующим   образом:   Р2 =  8 кВт,   Рз  =  3 кВт,    Р4  =  1кВт,

               Тема 2. 5. Кручение. Внутренние силовые факторы при кручении                      219

 

вал вращается с постоянной скоростью ώ = 25 рад/с. Построить эпюру крутящих моментов на валу.

                

Решение

1. Определяем моменты пар сил на шкивах. Вращающий момент определяем из формулы мощности при вра­щательном движении

                                               

Момент на шкиве1 движущий, а моменты на шкивах 2, 3, 4 — моменты сопротивления механизмов, поэтому они имеют противо­положное направление. Брус скручивается между движущим момен­том и моментами сопротивления. При равновесии момент движущий равен сумме моментов сопротивления:

 

        

220                                                                                    Лекция 26

2. Определяем крутящие моменты в поперечных сечениях бруса
с помощью метода сечений.

      

Сечение I (рис. 26. 4а):

- m4 + М_К1 = 0; М_К1 = m4; М_К1 = 40Н • м — крутящий момент отрицательный.

Сечение II (рис. 26. 4b):

- m4 – т₃ + М_К2 = 0; М_К2 = m4 + m3; М_К2 = 40 + 120 = 160Н•м — крутящий момент отрицательный.

Сечение III (рис. 26. 4в):

- m4 – т₃ + т1 — М_кз = 0; -М_кз = m4 + т₃ - т1;

-М_кз = 40 + 120 - 480; М_Кз = 320 Н • м — крутящий момент поло­жительный.

Сечение IV:

M_K4 = - m4 – т₃ + т1   – т₂= 0.

3. Строим эпюру крутящих моментов. Заметим, что скачок на
эпюре всегда численно равен приложенному вращающему моменту.

Выбираем соответствующий масштаб.

Откладываем значения моментов, штрихуем эпюру поперек, об­водим по контуру, записываем значения моментов (см. эпюру под схемой вала (рис. 26. 3)). Максимальный крутящий момент на участ­ке IIIМкз =320Н•м.

Пример 2.   Выбрать рациональное расположение колес на валу (рис. 26. 5). т1= 280 Н • м; т₂ = 140 Н • м; т₃ = 80 Н • м.

Примечание. Меняя местами колеса (шкивы) на валу, можно изменять величины крутящих моментов. Рациональным рас­положением является такое, при котором крутящие моменты принимают минимальные из возможных значения.

        m0 = т₁ + т2   + т₃ = 280 + 140 + 80 = 500 Н • M.

                Тема 2. 5. Кручение. Внутренние силовые факторы при кручении                      221

 

Рассмотрим нагрузки на валу при различном расположении колес.

Из представленных вариантов наиболее рационально располо­жение шкивов в третьем случае, здесь значения крутящих момен­тов минимальны. Вывод: при установке шкивов желательно, чтобы мощность подавалась в середине вала и по возможности равномерно распределялась направо и налево.

 

    

 

     Контрольные  вопросы   и задания

1. Какие деформации возникают при кручении?

2. Какие гипотезы выполняются при деформации кручения?

3. Изменяются ли длина и диаметр вала после скручивания?

222                                                                                          Лекция 26

4. Какие внутренние силовые факторы возникают при кручении?

5. Что такое рациональное расположение колес на валу?

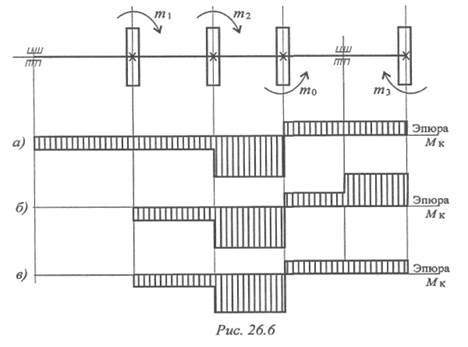
6. Для заданного вала (рис. 26. 6) выбрать соответствующую
эпюру крутящих моментов (а, б, в). m1 = 40Н•м; т2 = 180Н•м;
m₀ = 280Н•м.

  

 

7. В каком порядке рациональнее расположить шкивы на валу
для уменьшения нагрузки на вал (рис. 26. 7)?

 

     

                                                                                        Тема 2. 5. Кручение                                                                                        223

ЛЕКЦИЯ 27

Тема 2. 5. Кручение.

Напряжения и деформации

при кручении

Иметь представление о напряжении и деформациях при круче­нии, о моменте сопротивления при кручении.

Знать формулы для расчета напряжений в точке поперечного сечения, закон Гука при кручении.

Напряжения при кручении

Проводим на поверхности бру­са сетку из продольных и попе­речных линий и рассмотрим рису­нок, образовавшийся на поверхно­сти после деформации (рис. 27. 1а). Поперечные окружности, оставаясь плоскими, поворачиваются на угол φ, продольные линии искривляют­ся, прямоугольники превращают­ся в параллелограммы. Рассмотрим элемент бруса 1234 после деформа­ции.

                                   

                     

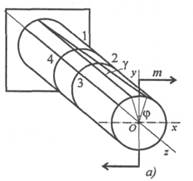
При  выводе    формул    используем    закон    Гука    при    сдвиге    и    гипотезу

224                                                                       Лекция 27

плоских сечений и неискривления радиусов поперечных сечений.

При кручении возникает напряженное состояние, называемое «чистый сдвиг» (рис. 27. 16).

При сдвиге на боковой поверхности элемента 1234 возникают касательные напряжения, равные по величине (рис. 27. 1в), элемент деформируется (рис. 27. 1г).

Материал подчиняется закону Гука. Касательное напряжение пропорционально углу сдвига.

Закон Гука при сдвиге τ = Gγ,

G — модуль упругости при сдвиге, Н/мм²; γ -- угол сдвига, рад.

⇐ Предыдущая42434445464748495051Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: