Полярный  момент инерции  круга

                          Полярный  момент   инерции  круга

Для круга вначале вычисляют поляр­ный момент инерции, затем — осевые.

Представим круг в виде совокупности бесконечно тонких колец (рис. 25. 3).

Площадь каждого кольца можно рас­считать как площадь прямоугольника с длинной стороной, равной длине соответ­ствующей окружности, и высотой, равной толщине кольца: dA = 2π p dp.

Подставим это выражение для площа­ди в формулу для полярного момента инерции: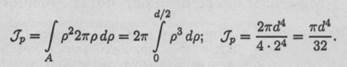            

Получим формулу для расчета полярного момента инерции круга:

               

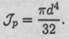
Подобным же образом можно получить формулу для расчета полярного момента инерции кольца:

                                              

где d — наружный диаметр кольца; d_BH — внутренний диаметр ко­льца.

Если обозначить d_BH/d = с, то

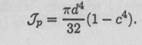
212                                                                 Лекция 25

         Осевые моменты инерции круга и кольца

Используя известную связь между осевыми и полярными момен­тами инерции, получим:

   

      

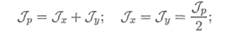
      Моменты инерции относительно параллельных осей

Оси Ox0 и Ох параллельны (рис. 25. 4).

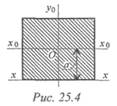При параллельном переносе прямоугольной системы осей уоОхов новое положение уоОх зна­чения моментов инерции J_x, J_y, J_xy заданно­го сечения меняются. Задается формула перехода без вывода.

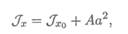здесь J_x — момент инерции относительно оси Ох;

                                   J_X0— момент инерции относительно оси Ox0;  

 А — площадь сечения;

а — расстояние между осями Ох и Ox0.

            Главные оси и главные моменты инерции

Главные оси — это оси, относительно которых осевые момен­ты инерции принимают экстремальные значения: минимальный и максимальный.

Главные центральные моменты инерции рассчитываются отно­сительно главных осей, проходящих через центр тяжести.

Примеры решения задач

Пример 1. Определить величину осевых моментов инерции плоской фигуры относительно осей Ох и Оу (рис. 25. 5).

                  Тема 2. 4. Геометрические характеристики плоских сечений                     213

                                                                                                                                                                                                                     

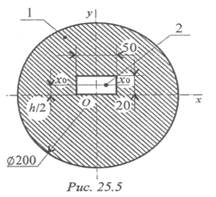                                                                                                      Решение

   1. Определим осевой момент инерции относительно оси Ох. Ис­пользуем формулы для главных центральных моментов. Предста­вим момент инерции сечения как разность моментов инерции круга и прямоугольника.

            bh³

   Для прямоугольника J_X02 = ——.

                                                                                                                   12

Для прямоугольника ось Ох не проходит через ЦТ.

Момент инерции прямоугольника относительно оси Ох:

             

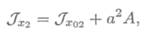
где А — площадь сечения; а — расстояние между осями Ох и Ox0.

            

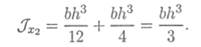
Момент инерции сечения

           

       

2. Осевой момент инерции относительно оси Оу:

            

Момент инерции сечения

               

214                                                              Лекция 25

Пример 2. Найти главный центральный момент инерции сече­ния относительно оси Ох (рис. 25. 6).

                                        Решение

     1. Сечение составлено из стандарт­ных профилей, главные центральные моменты инерции которых приводятся в таблицах ГОСТ, см. Приложение 1.

    Для двутавра № 14 по ГОСТ 8239-89 Jo_x1 = 572 см⁴.

    Для швеллера № 16 по ГОСТ 8240-89 Jox₂ = 757 см⁴.

    Площадь А2 = 18, 1 см², Joy₂ = 63, 3 см⁴.

2. Определяем координату центра тяжести швеллера относительно оси Ох. В заданном сечении швеллер повернут и поднят.
При этом главные центральные оси поменялись местами.

y2 = (h1/2) + d2 — zo₂; по ГОСТ находим h1 = 14 см; d2 = 5 мм; zo = 1, 8 см.

3. Момент инерции сечения равен сумме моментов инерции
швеллеров и двутавра относительно оси Ох. Используем формулу
моментов инерции относительно параллельных осей:

В данном случае J ´ q_X2 =  J ´ qу₂  =  63, 3 см⁴;

y2 = (14/2) + 0, 5 — 1, 8 = 5, 7 см (расстояние между осями координат Ох' и Ох);

            

Контрольные   вопросы   и   задания

1. Диаметр сплошного вала увеличили в 2 раза. Во сколько раз
увеличатся осевые моменты инерции?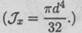

2. Осевые моменты сечения равны соответственно J_x = 2, 5 мм⁴ иJy = 6, 5 мм. Определите полярный момент сечения.

3. Осевой момент инерции кольца относительно оси Ох J_x = 4 см⁴. Определите величину J_p.

                Тема 2. 4. Геометрические характеристики плоских сечений                   215

 

4. В каком случае J_x наименьшее (рис. 25. 7)?

        

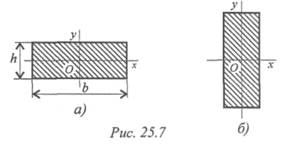
5. Какая из приведенных формул для определения J_x подойдет
для сечения, изображенного на рис. 25. 8?

               

6. Момент инерции швеллера № 10 относительно главной центральной оси J_Xo = 174см⁴; площадь поперечного сечения 10, 9 см².

Определите осевой момент инерции относительно оси, проходя­щей через основание швеллера (рис. 25. 9).

7. Сравнить полярные моменты инерции двух сечений, имею­щих практически одинаковые площади (рис. 25. 10).

8. Сравнить осевые моменты инерции относительно оси Ох пря­моугольника и квадрата, имеющих одинаковые площади (рис. 25. 11).

 

          

216                                                                   Лекция 26

ЛЕКЦИЯ 26

                            

⇐ Предыдущая40414243444546474849Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: