Тема 2.5. Кручение.  . Внутренние силовые факторы  при кручении.    Построение эпюр крутящих моментов. Деформации при кручении

                          Тема 2. 5.   Кручение.  

Внутренние силовые   факторы  при   кручении.

      Построение   эпюр крутящих   моментов

Иметь представление о деформациях при кручении, о внутрен­них силовых факторах при кручении.

Уметь строить эпюры крутящих моментов.

Деформации при кручении

Кручение круглого бруса происходит при нагружении его па­рами сил с моментами в плоскостях, перпендикулярных продольной оси. При этом образующие бруса искривляются и разворачиваются на угол γ называемый углом сдвига (угол поворота образующей). Поперечные сечения разворачиваются на угол φ, называемый углом закручивания (угол поворота сечения, рис. 26. 1).

Длина бруса и размеры поперечного сечения при кручении не изменяются.

                             

                Тема 2. 5. Кручение. Внутренние силовые факторы при кручении                     217

 

Связь  между угловыми   деформациями  определяется   соотноше­нием

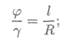                              l— длина бруса; R — радиус сечения.

Длина бруса значительно больше радиуса сечения, следователь­но, φ » γ.

Угловые деформации при кручении рассчитываются в радиа­нах.

Гипотезы при кручении

1. Выполняется гипотеза плоских сечений: поперечное сечение бруса, плоское и перпендикулярное продольной оси, после деформа­ции остается плоским и перпендикулярным продольной оси.

2. Радиус, проведенный из центра поперечного сечения бруса, после деформации остается прямой линией (не искривляется).

3. Расстояние между поперечными сечениями после деформации не меняется. Ось бруса не искривляется, диаметры поперечных се­чений не меняются.

               Внутренние силовые факторы при кручении

Кручением называется нагружение, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор — крутящий момент.

Внешними нагрузками также являются две противоположно на­правленные пары сил.

Рассмотрим внутренние силовые факторы при кручении круг­лого бруса (рис. 26. 1).

Для этого рассечем брус плоскостью I и рассмотрим равновесие отсеченной части (рис. 26. 1а). Сечение рассматриваем со стороны отброшенной части.

Внешний момент пары сил разворачивает участок бруса про­тив часовой стрелки, внутренние силы упругости сопротивляются повороту. В каждой точке сечения возникает поперечная сила dQ (рис. 26. 16). Каждая точка сечения имеет симметричную, где возни­кает поперечная сила, направленная в обратную сторону. Эти   силы образуют   пару   с   моментом    dm =  pdQ;   p  —  расстояние  от  точки

218                                                                 Лекция 26

до центра сечения. Сумма поперечных сил в сечении равна нулю: . Σ dQ = 0.

С помощью интегрирования получим суммарный момент сил упругости, называемый крутящим моментом:

              

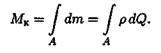
Практически крутящий момент определяется из условия равно­весия отсеченной части бруса.

Крутящий момент в сечении равен сумме моментов внешних сил, действующих на отсеченную часть (рис. 26. 1в):

                   

          Эпюры крутящих моментов

Крутящие моменты могут меняться вдоль оси бруса. После определения величин моментов по сечениям строим график-эпюру крутящих моментов вдоль оси бруса.

Крутящий момент считаем положительным, если моменты внешних пар сил направлены по часовой стрелке, в этом случае мо­мент внутренних сил упругости направлен против часовой стрелки (рис. 26. 2).

                             

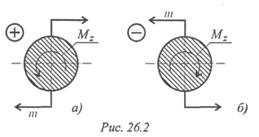
Порядок построения эпюры моментов аналоги­чен построению эпюр про­дольных сил. Ось эпюры параллельна оси бруса, значения моментов откла­дывают от оси вверх или вниз, масштаб построе­ния выдерживать обязательно.

⇐ Предыдущая41424344454647484950Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: