Ориентировочно число групп равно √100, из объёма выборки, оно не должно быть менее 5 и болем 20. В нашем случае оно равно 8.

Ориентировочно число групп равно √ 100, из объёма выборки, оно не должно быть менее 5 и болем 20. В нашем случае оно равно 8.

 Расчеты параметров вариационного ряда

n – численность ряда у нас = 100 (10 × 10) или f;

(сумма частот равна объёму совокупности ∑ f = n = 100;

Х × f = ∑ f x – всего всходов подсолнечника (насчитали 300 шт. );

Х  - среднее арифметическое значение  = (å fх)/n = 300/100 = 3.

å × f× (X- ) = -47 + 47 = 0 (å всех отклонений от средней арифмет. всегда =0);

å × f× (X- )² = 164 – сумма квадратов отклонений от средней арифметической;

S²(g²), дисперсия = å × f× (X- )² /(n-1) = 164/99 = 1, 65;

S(g), среднее квадратическое отклонение от  = = = ± 1, 28;

S – мера разброса отдельных наблюдений (замеров) вокруг среднего значения признака. Чем больше дисперсия или стандартное отклонение, тем больше рассеяны индивидуальные значения признака около средней, т. е. больше изменчивость, и наоборот.

S – стандартное отклонение – показатель, характеризующий наиболее вероятную среднюю ошибку отдельного, единичного наблюдения, взятого из данной совокупности. В пределах одного значения (± 1 S) укладывается ≈ 2/3 всех наблюдений, или 68, 3% всех вариант, т. е. основная часть изучаемого ряда величин. => S называется основным отклонением вариационного ряда. => возможны отклонения от X, превосходящие (± 1 S), но их вероятность по мере удаления отклонений от (± 1 S) все время уменьшается. Вероятность встретить варианту, отклоняющуюся от Х на величину > (± 3S) ≈ 0, 3%.

Утроенное значение стандартного отклонения считается предельной ошибкой отдельного наблюдения, т. е. практически все значения вариант в вариационном ряду лежат в пределах (± 3S). Числовой коридор (± 3S) даёт ясное представление о широте ряда наблюдений, его рассеянии.

V, коэффициент вариации  =       S × 100 = (1, 28/3)× 100 = 42, 7%;

                                                     x

S x, ошибка выборочной средней = =  =  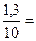0, 13.

Т. е. пределы колебания х. В нашем случае Sx = 3 ± 0, 13 растений, т. е. возможные колебания её от 2, 87 до 3, 13.

 Sx – ошибка выборочной средней (выборки) – это мера отклонения выборочной средней Х от средней всей (генеральной) совокупности µ. Sх возникает вследствие неполной репрезентативности (представительности) выборочной совокупности. Величина Sх зависит от степени изменчивости изучаемого признака и от объёма выборки. Чем больше S, тем больше Sх, и чем больше число измерений n, тем меньше Sx.

    Ошибку выборки выражают в тех же единицах, что и варьирующий признак и приписывают к соответствующим средним со знаком ±, х ± Sx.

S x %, относительная ошибка выборочной средней (точность вычисления) = Sx =  × 100%. В нашем случае  Sx = = 4. 3%.

Рис. 6. 1. Кривая вариационного ряда

Выводы

1. Среднее количество всходов на 1 пог. м. = 3+0, 128, т. е. при повторных подсчетах оно может колебаться в пределах 2, 872-3, 128.

2. Густота посевов не выровнена, V значительный (42, 7%, более 20%).

3. Точность вычисления (анализа) – удовлетворительная (4, 3%).

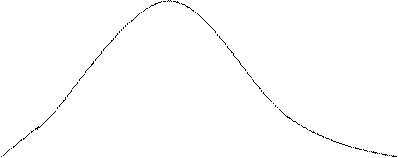
Кривая вариационного ряда близка к синусоиде, т. е. к нормальному распределению.                                            Для справки:

 если V < 10% - варьирование незначительное;

                         если 10%< V< 20% - варьирование среднее;

                         если  V> 20% - варьирование значительное;

    если    Sx% < 2% - отличная точность вычисления;

    если 2 < Sx% < 4% - хорошая точность вычисления;

    если 4 < Sx% < 5% - удовлетворительная точность вычисления;

    если    Sx% > 5 % - низкая точность вычисления.                    

Задача: Составить непрерывный вариационный ряд значений замера

            диаметра корзинки подсолнечника (табл. 3, 4).

Замеры диаметра корзинки подсолнечника проводились в фазу спелости (восковая окраска тыльной стороны) в 5-ти местах по 10 растений подряд.

Таблица 3. Диаметр корзинки подсолнечника, см

Ряд, №	№ растения
	I	II	III	IV	V	VI	VII	VIII	IX	X
	18, 5	19, 2	19, 4	22, 0	18, 6	18, 9	19, 3	20, 1	19, 8	20, 3
	18, 7	18, 5	15, 5	18, 9	18, 5	18, 5	19, 4	20, 8	20, 2	19, 8
	19, 1	16, 8	18, 4	18, 9	17, 0	20, 0	21, 2	18, 1	17, 9	19, 6
	19, 4	18, 9	19, 3	17, 2	19, 4	18, 7	20, 0	20, 2	19, 5	20, 3
	17, 8	17, 6	21, 0	18, 0	18, 2	17, 9	18, 1	22, 4	18, 0	17, 5

X_min, наименьший диаметр = 15, 5 см.

X_max, наибольший диаметр = 22, 4 см.

X_max - X_min = 6. 9 »7 cм.

Выделяем 7 классов с разницей = 1 см и группируем в них замеры.

Таблица 4. Составление и обработка вариационного ряда

Х	Хv среднее	f	fXv	X2v	fXv
15, 5-16, 4
16, 5-17, 4
17, 5-18, 4
18, 5-19, 4
19, 5-20, 4
20, 5-21, 4
21, 5-22, 4
å	-			-

Расчеты: х – среднее арифметическое = å fX_v/n = 954/50 = 19, 1 см;

         C – корректирующий фактор = (å fX_v)²/n = 954²/50 = 18202;

          S² – дисперсия = (å fX²_v –С)/n-1 = (18274-18202)/50-1 = 1, 46;

          S – среднее квадратическое отклонение = = = ±1, 2 см;

          V – коэффициент вариации = (S/x)× 100 = (1, 2/19, 1)× 100 = 6, 3%;

          – ошибка средней = S/Ö n = 1, 2/Ö 50 = ±0, 17 см;

          % - относительная ошибка (точность) =  = 0, 9%.

Выводы

1. Средний размер диаметра корзинки подсолнечника составляет 19, 1±0, 17 см (18, 93-19, 27).  

2. Варьирование вариационного ряда – слабое (V< 10%).

  3. Точность определения – отличная (< 2%).

 

 

⇐ Предыдущая13141516171819202122Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: