Лекция №7.. Теоретические распределения. Дисперсионный анализ. Корреляционный и регрессионный анализ.

Лекция №7.

Теоретические распределения. Дисперсионный анализ. Корреляционный и регрессионный анализ.

    В основе эмпирических распределений (распределение результатов измерений, полученных при изучении выборки) лежат определенные математические закономерности, которые в генеральной совокупности (при n→ ∞ ) характеризуются некоторыми теоретическими закономерностями. На основе теоретических распределений построены статистические критерии, которые используются для проверки некоторых гипотез. Чаще всего в НИР опираются на нормальное распределение или специальные распределения, полученные из нормального, для конкретно поставленной задачи и при ограниченном числе степеней свободы (критерий t, F, χ ², Пуассона).

    Для нормального (гауссового) распределения характерно:

в области µ ± ϭ лежит 68, 26% (2/3) всех значений всех наблюдений;

внутри пределов µ ± 2ϭ – 95, 46% всех значений случайной величины;

интервал µ ± 3ϭ охватывает 99, 73% => практически все значения, где

µ - генеральная средняя, которая находится в центре распределения;

ϭ – стандартное отклонение, измеряет вариацию отдельных наблюдений около средней генеральной совокупности.

В практике агрономических исследований можно пользоваться вероятностями 0, 95 – 95% и 0, 99-99%, которые соответствуют 0, 05-5%-ному и 0, 01-1%-ному уровням значимости.

Чем стандартное отклонениеϭ больше, => больше варьирует изучаемый материал, и => более пологой становится вариационная кривая, а при малых значениях ϭ она приобретает иглообразную форму.

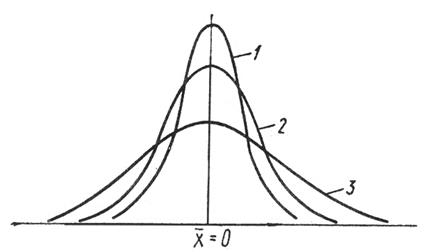
Рис. 1. Нормальныекривые (1, 2, 3) при разныхзначениях параметра s (Лакин Г. Ф., 1990).

t-распределение Стьюдента. Закон нормального распределения проявляется при n> 20-30. Однако часто экспериментатор проводит ограниченное число измерений, основывает свои выводы на малых выборках. В 1908г. английский химик В. Госсет открыл закон t-распределения для выборочных средних, определяемый по формуле:

х - µ        х - µ

t =      =        ,

      S           Sx

                   √ n

где в числителе отклонение выборочной средней от средней генеральной совокупности, а в знаменателе – стандартная ошибка всей генеральной совокупности.

При увеличении n> 30распределение t приближается к нормальному и переходит в него при n→ ∞.

Распределение t-Стьюдента очень важно в работе с малыми выборками: позволяет определить доверительный интервал, накрывающий среднюю арифметическую всей совокупности µ, и проверить ту или иную гипотезу относительно генеральной совокупности.

F-распределение Фишера. Если у нормально распределенной совокупности взять 2 независимые выборки объемом n₁ и n₂ и подсчитать дисперсии S₁²и S₂² со степенями свободы ν ₁ = n₁ - 1и ν ₂ = n₂ – 1, то можно определить отношение дисперсий: F = S₁²/ S₂². Отношение дисперсий берут таким, чтобы в числителе была большая дисперсия, и => F≥ 1.

В дисперсионном анализе соотношение дисперсии вариантов S_V² / S_Z², является основным критерием, дающим общую оценку достоверности разниц между средними арифметическими или общую оценку достоверности опыта. F = S_V²: S_Z². Вычисленный критерий F₀₅ (фактический) сравнивают с теоретическимF_табл. . ЕслиF_факт. ≥ F_теор. , в опыте доказана достоверность различий между средними арифметическими, т. е. в опыте одна или несколько пар вариантов, между средними х которых есть достоверная разница, а если F_факт. < F_теор, то она отсутствует.

Дисперсионный анализ – основной и наиболее распространённый метод математической обработки результатов исследований. Он позволяет оценить методику исследований по величине относительной ошибки (точности) – S 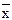%, и достоверность разницы между вариантами.

Если Sx% менее 2%, точность отличная, нарушений методики нет.

Если 2 < Sx% < 4% - хорошая точность;

если 4 < Sx% < 5% - удовлетворительная точность;         

если Sx% более 5% - точность опыта низкая.

Если разница между вариантами больше (с плюсом или минусом) НСР – она существенна, меньше НСР – несущественна.

1. Пример статистической обработки урожайных данных исследований методом дисперсионного анализа в однофакторном полевом опыте: ”Влияние боронования на урожай подсолнечника”

Условные (статистические) обозначения:

l – число вариантов в опыте;

n – количество повторений;

Х – поделяночный урожай;

Х – средний урожай по вариантам;

Х_p - средний урожай по повторениям;

Х₀ – средний урожай по опыту;

d – разница между вариантами и контролем;

А – произвольное начало (округленное до целого числа значение ₀ );

V – сумма по вариантам;

Р – сумма по повторениям;

V_A – cумма отклонений от А по вариантам;

Р_А – сумма отклонений от А по повторениям;

С – корректирующий фактор;

С_У – общее варьирование (общая дисперсия);

С_V - варьирование вариантов (дисперсия вариантов);

С_Р – варьирование повторений (дисперсия повторений);

С_Z – случайное варьирование (остаточная дисперсия);

n - число степеней свободы;

Sx – ошибка опыта;

Sx % - точность опыта (относительная ошибка);

НСР₀₅ – наименьшая существенная разность (для 5%-го уровня

          значимости);

å - сигма, знак суммирования;

F₀₅ – критерий Фишера F;

t₀₅ - критерий Стьюдента t;

Н₀ – нулевая гипотеза.

Исходные данные и расчетные показатели оформляются в таблицу.

№ вар.	Варианты	Х	V	X	d	X-A	VA	(X-A)2	V2A
		І ІІ ІІІ IV				І ІІ ІІІ IV		І ІІ ІІІ IV
								å (X-A)2	å V2A
	P XP							å p2A	[å (X-A]2

Порядок проведения расчетов по дисперсионному анализу.

І. Средний урожай по опыту = ₀=Σ Х/n∙ l = 263, 1 / 4^. 3=21, 9 (табл. 5).

ІІ. Произвольное начало = А = 22 (округлённое до целого числа ₀).

ІІІ. Общая сумма квадратов отклонений от А = å (Х-А)² =    

=2, 25+2, 25+0, 36+0, 01+0, 01+1, 00+0, 16+0, 09+0, 36+0, 64+0, 64 = 7, 77.

IV. Сумма квадратов отклонений от А по вариантам = V_A² =

=13. 64+2. 25+1. 69 = 17, 63.

V. Сумма квадратов отклонений от А по повторениям = Р_А² =

=1, 44+4, 00+1, 44+1, 21 = 8, 09.

VI. Квадрат суммы отклонений от А = [å (X-A)]² = 0, 9² = 0, 81.

VII. Корректирующий фактор = С = [å (X-A)]²/l× n = 0, 81/12 = 0, 07.

VIII. Общая дисперсия = С_У = Σ (Х-А)²-С = 7, 77-0, 07 = 7, 70 =100%.

IX. Дисперсия повторений = С_Р = Σ Р²_А/l – C = 8, 09: 3 – 0, 07 = 2, 63=34%.

Х. Дисперсия вариантов = С_V  = Σ V²_A/n – C = 17, 63: 4 – 0, 07 = 4, 34=56%.

ХІ. Остаточная дисперсия = С_Z = C_У – (С_Р + С_V) = 7, 70 – 6, 97 = 0, 73=10%.

Результаты дисперсионного анализа

Дисперсия	Сумма квадратов	Число степеней свободы	Средний квадрат S2	F05
				факт.	табл.
Общая – СУ Повторений-СР Вариантов - СV	7, 70 2, 63 4, 34	(ln-1) = 11 (n-1) = 3 (l-1) = 2	- - СV: (L-1)=2, 17	18, 08	5, 14
Остаточная-СZ	0, 73	(l-1)(n-1)=6	СZ/(n-1)(L-1)= =0, 12	-	-

 

Таблица 5. Статистическая обработка урожайных данных методом дисперсионного анализа

 

Варианты опыта	Х				V		d	X – A				VА	(X – A)2				VА2
	I	II	III	IV				I	II	III	IV		I	II	III	IV
Без боронования	20, 5	20, 5	21, 4	21, 9	84, 3	21, 1	-	-1, 5	-1, 5	-0, 6	-0, 1	-3, 7	2, 25	2, 25	0, 36	0, 01	13, 69
Боронование до всходов	22, 0	22, 1	23, 0	22, 4	89, 5	22, 4	+1, 3	0, 0	+0, 1	+1, 0	+0, 4	+1, 5	0, 00	0, 01	1, 00	0, 16	2, 25
Боронование по всходам	22, 3	21, 4	22, 8	22, 8	89, 3	22, 3	+1, 2	+0, 3	-0, 6	+0, 8	+0, 8	+1, 3	0, 09	0, 36	0, 64	0, 64	1, 69
Р	64, 8	64, 0	67, 2	67, 1	263, 1	21, 9	РА	-1, 2	-2, 0	+1, 2	+1, 1	-0, 9	1, 44	4, 00	1, 44	1, 21	0, 81
р	21, 6	21, 3	22, 4	22, 4	0	21, 9

 

Вывод 1-й. Если F_факт> F_табл, то нулевая гипотеза отвергается, между

               вариантами есть существенные различия, а если F_факт< F_табл,

               то нулевая гипотеза подтверждается и между вариантами нет

               существенных различий. В нашем опыте F_фактзначительно

               больше F_табл, следовательно, нулевая гипотеза отвергается и

               между вариантами имеются существенные различия.

Расчеты. S 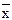 = = = 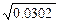±0, 17 ц/га (ошибка опыта).

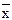           S % = S 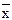/ 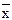₀× 100 = 0, 17/21, 9× 100 = 0, 8 % (точность опыта).

НСР₀₅ = S 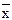× × 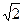t₀₅ = 0, 17× 1, 4× 2, 45 = 0, 6ц/га.

n = (n-1)(l-1) = 3× 2 = 6 t₀₅ = 2, 45.

⇐ Предыдущая14151617181920212223Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: