 |
Базис векторного пространства
|
|
|
|
Определение и простейшие свойства векторных пространств
Непустое множество V называется векторным
(линейным) пространством над полем P, если:
1) на V задана бинарная алгебраическая операция "+";
2) определено умножение элементов из V на элементы из P, т.е.
задано отображение P×V →V: (α,v) Þ α⋅v.
Эти операции должны удовлетворять следующим требованиям (аксиомам), выполняющимся для любых элементов x,y,z∈V и α,β∈P:
1. x+y=y+x (коммутативность).
2. (x+y)+z=x+(y+z) (ассоциативность).
3. Существует элемент 0∈V такой, что 0+x=x+0 для любого x∈V.
Элемент 0 называется нулевым элементом (вектором).
4. Для каждого x∈V существует противоположный элемент −x, такой, что x+(−x)=0.
5. 1x=x.
6. (αβ)x=α(βx).
7. (α +β)x=αx+βx.
8. α(x+y)=αx+αy.
Элементы из V называют векторами, а элементы поля P – скалярами (числами). Совокупность аксиом 1–4 означает,
что множество V с операцией сложения "+" является абелевой группой.
Если даны два вектора x,y∈V, то под разностью
x−y будем понимать x−y=x+(−y).
Некоторые свойства векторных пространств:
1) Значение суммы комплексного числа векторов не зависит от порядка суммирования (например, по аксиоме 2).Поэтому операцию сложения векторов можно распростронить на любое конечное число векторов.
2) Произведение нулевого вектора на любое число a из основного поля равно нулевому вектору, т.е. a×0=0. Действительно,
a×0=a×(0+0)=a×0+a×0.Следовательно,a×0=a×0-a×0=0.
3) Произведение любого вектора x на число 0 рано нулевому вектору,т.е. x×0. Действительно,x×0=x×(0+0)=x×0+x×0,откуда:
x×0=x×0-x×0=0.
4) Если αx=0,то либо α=0,либо х=0.В самом деле,если α ¹ 0, то
х =1х=[(1/α)×α]×х=(1/α)(αх)=(1/α)×0=0.
|
|
|
5) Для каждого вектора х противоположный вектор равен произведению х на число -1, т.е. –х= -1х. В самом деле,
х+(-1)х=1х+(-1)х=(1-1)х=0х=0. Означает, что вектор (-х) является противоположным к вектору х.
6) Для любого вектора х и любого числа α выполняется равенство α(-х)=(-αх).Действительно,
α(-х)= α[(-1)х]= [α(-1)]х= (-1)(αх) =(-αх).
7) Для любых векторов х и у и любого числа α выполняется равенство α(х-у)= αх- αу.В самом деле,
α(х-у)= α[х+(-у)]= αх+ α(-у)= αх- αу.
8) Для любого вектора х и любых чисел α,β выполняется равенство
(α- β)х= αх- βх, так как
(α −β)x=[α +(−β)]x=αx+(−β)x=αx−βx.
Лиинейная зависимость векторов
Конечная система векторов х1, …,хs называется линейно зависимой, если существуют, такие числа α 1, …, α s, не все равную нулю, что
у= α1х1 + … + αsхs.
В противном случае система векторов х1 , …, хs линейно независима.
Теорема 2.1 Если некоторая подсистема заданной системы векторов линейно зависима, то и вся система векторов линейно зависима.
Теорема 2.2 каждый вектор заданной системы векторов S линейно выражается через векторы любой ее максимальной линейно независимой подсистемы.
Д-во.
Пусть х1, …,хn – максимально линейно независимая под система в системе векторов S и b – произвольный вектор в S.
Тогда α1х1 + … + αnхn + αb = 0, α ¹ 0.
Так как α ¹ 0, то неравенство α1х1 + … + αnхn + αb = 0 можно преобразовать к виду
b = -(α1/ α) х1 - … - (αn / α) хn, т.е. получить линейное выражение вектора b через вектор х1, …,хn Теорема доказана.
Теорема 2.3 (Основная теорема о линейной зависимости векторов)
Пусть даны системы векторов х1, …,хr и y1, …,ys, причем первая линейная зависимость выражается через вторую. Тогда число векторов в первой системе превышает числа векторов во второй, т.е. r£s.
Теорема 2.3 (теорема о рангах двух систем векторов)
|
|
|
Пусть даны две системы, причем ранг первой равен k, а ранг второй – r. Если первая система линейно выражается через вторую, то k £ r. Если две системы эквивалентны, то k =r.
Линейная выражаемость системы векторов
Система векторов х1, …,хs, s³2 линейно зависима тогда и только тогда, когда хотя бы один из ее векторов линейно выражается через остальные векторы.
Действительно, если система векторов х1, …,хs линейно зависима, то выполняется равенство α1х1 + … + αsхs=0, в котором, например, хs ¹ 0.
Тогда из этого равенства получаем:
хs= -(α1/ αs) х1 - … - (αs-1 / αs) хs-1. Это означает, что ветор хs линейно выражается через систему векторов х1, …,хs-1, т.е.
хs =α1х1 + … + αs-1 хs-1
Тогда верно и равенство α1х1 + … + αsхs=0, в котором αs= -1 ¹ 0. Значит, система векторов х1, …,хs линейно зависима.
Базис векторного пространства
Векторное пространство называют конечномерным, если в нем есть линейно независимая система, состоящая из n векторов, а любая конечная система из большего числа линейно зависима.
Если такого числа нет, т.е. если для любого числа n в векторном пространстве существует линейно независимая система из n векторов, то такое векторное пространств называют бесконечным.
Всякую конечную упорядоченную систему векторов векторного пространства V называют базисом, если эта система линейно независима и любой вектор векторного пространства линейно выражается через векторы этой системы.
Теорема 3.1 Пусть векторное пространство Хn обладает базисом
e1, …, еn. тогда любой вектор х из Vn единственным образом представляется в виде х=х1е1 + … + хnеn = (е1, …, еn) 
= e [x]. Теорема 3.2. Все базисы конечномерного векторного пространства V
состоят из одинакового количества векторов.
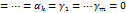
Доказано, система 
линейно независима и является базисом в подпространстве L1+L2.
, 
, 
, то
= 
= 
= 
. Теорема доказана.
|
|
|
