 |
Определение и простейшие св-ва линейных операторов
|
|
|
|
Пусть даны линейные пространства X и Y над одним и тем же полем P. Говорят, что из пространства X в пространство Y действует оператор 
, если каждому вектору а из Х по какому-либо правилу ставится в соответствие определенный вектор а1= (а) = а из Y. Вектор а1 образом вектора а, вектор а – прообразом вектора а1 при отображении .
Оператор действующий из из X в Y, называют линейным, если он сумму любых векторов a и b из Х переводит в сумму их образов а1 и b1, а произведение любого вектора а из Х на любое число a из P – в произведение образа а1 вектора а на то же число a, т.е. если
= 
+ 
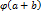= а1 + b1, 
= 
= 
а1
Из определения линейного оператора вытекают следующие утверждения:
1) линейный оператор приводит линейную комбинацию векторов
из Х в линейную комбинацию образов 
этих векторов с теми же коэффициентами, т.е.
= 
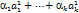
2) линейный оператор 
переводит нулевой вектор 0 из Х в нулевой вектор 01 из Y
Д-во:
3) линейный оператор переводит вектор –а, противоположеный вектору а, в вектор –а1, противоположный вектору а1= a
Д-во:
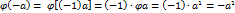
Теорема 19.1. Пусть линейный оператор действует из линейного пространства Х в линейное пространство Y и 
– базис в Х.
Тогда оператор определяется с заданием образов 
векторов базиса .
Действие с линейными операторами
Пусть из линейного пространства Х над полем Р в линейное пространство Y над тем же полем действуют линейные операторы и w считаются равными, если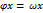 
, xÎX.
Суммой операторов и w называют оператор + w, т.е.
, xÎX
Действительно, для любых векторов у,xÎX имеем:
Для любого вектора xÎX и числа lÎР:
Произведением линейного оператора на число lÎР называют оператор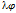 
, т.е. 
, xÎX
Действительно, для любых векторов у,xÎX и любого числа mÎР имеем:
|
|
|
1) 
2) 
Матрица линейного оператора
Предположим, что в линейном пространстве X задан базис
, а в линейном пространстве Y – базис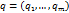 
. Каждый вектор такой по базису q:
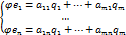
с матрицей
А= 
и назавем ее матрицей линейного оператора в паре базисов е и q.
Теорема 20.1. Пусть – линейный оператор, действующий из линейного пространства Х в линейное пространство Y имеющий в двух заданных базисах e в X и q в Y матрицу А. Тогда
1) ранг r оператора совпадает с рангом его матрицы А.
2) дефект оператора равен разности n – r размерности n линейного пространства Х и ранга r оператора .
3) сумма ранга и дефекта оператора равна размерности линейного пространства Х.
Соответствующие действия над операторами и матрицами
Изоморфизм линейного пространства
Биективное отображение 
векторных
пространств X и Y над полем P называется изоморфизмом, если для любых векторов x,y ∈ X и любого числа 
∈ P выполняются условия:
Отметим простейшие свойства изоморфизмов.
Свойство 1. Тождественное отображение 
, 
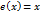является изоморфизмом.
Свойство 2. Если – изоморфизм, то обратное отображение 
также изоморфизм.
Действительно, поскольку 
– биективное отображение, то существует обратное отображение . Пусть x,y ∈ X. Так как биективно, то существуют элементы v,u ∈ X, такие, что
, 
.
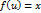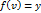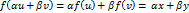
Следовательно,
, что и требовалось.
Свойство 3. Если и 
– изоморфизмы векторных
пространств, то 
– также изоморфизм.
Свойство 4. Для произвольного натурального n
= 
Свойство 5. 
= 0 тогда и только тогда, когда x = 0.
Действительно, если x = 0, то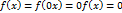 
.
Свойство 6. Если 
– линейно независимая система в X, то 
– линейно независимая система в Y, т.е. изоморфизм переводит линейно независимые системы в линейно независимые.
Свойство 7. Если – базис X, то – базис Y.
Теорема 5.1. Если векторные пространства V и W над полем имеют
|
|
|
одинаковую размерность, то они изоморфны.
Ранг и диффект линейного оператора
|
|
|
