 |
Жорданова нормальная форма
|
|
|
|
Вначале рассмотрим оператор 
, заданный в базисе
условиями 
Его матрица в этом базисе диагональная, и мы без труда можем указать все собственные значения, собственные векторы и инвариантные подпространства, однако в базисе
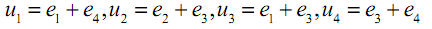
оператор имеет матрицу
и нахождение указанных объектов затруднительно. Таким образом, при изучении свойств оператора важно выбрать базис в котором матрица оператора имеет простой вид, такой вид называют нормальной формой матрицы (оператора). Какой вид считать простым определяется задачами, которые предполагается решать. Наиболее известной является жорданова нормальная форма матрицы.
Минимальный полином жордановой матрицы совпадает с ее
характеристическим полиномом тогда и только тогда, когда она не содержит двух клеток с одним λ
Жорданова матрица J, подобная (над P) матрице F, называется
её жордановой нормальной формой (ЖНФ).
Если для матрицы A существует ЖНФ над полем P, то все корни
характеристического полинома матрицы A лежат в поле P.
Построение Жордановой нормальной формы с единственным собственным значением
Алгоритм нахождения нормальной жордановой формы
1. Находим характеристический многочлен и ищем его корни.
2. Пусть l-один из корней, используя формулы L(l)=n-rang(A-lE)
И Lk(l)=rang(A-lE)k-1 -2 rang(A-lE)k+ rang(A-l E)k+1 находим все члены
произв порядка с l по диагонали.
3. Переходим к другому корню
4. Из всех полученных клеток Жордана строим Жорданову
нормальную форму матрицы.
Минимальный многочлен
Многочлен 
минимальной степени, имеющий старший коэффициент, равный единице, и аннулируемый матрицей А, называют минимальным многочленом этой матрицы.
Теорема 33.1. Любой многочлен, аннулируемый матрицей А, нацело делится на минимальный многочлен этой матрицы. В частности, характеристический многочлен матрицы делится на ее минимальный многочлен.
|
|
|
Д-во.
Разделим многочлен 
на минимальный многочлен с осьатком: 
, где многочлен 
имеет степень меньше степени 
. Заменив переменную 
матрицей А, получим:
Так как 
, то и 
. Это означает, что многочлен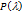 
нацело делится на 
Следствие. Любой корень минимального многочлена матрицы является корнем ее характеристического многочлена.
Теорема Гамильтона-Келли
Теорема 28.3. (теорема Гамильтона-Кэли)
Любая квадратная матрица является своего характерического многочлена.
Д-во.
Пусть А-квадратная матрица n-го порядка. Рассмотрим матрицу С к матрице 
. Матрицу С можно представить в виде
, где 
-некоторые числовые матрицы. По основному свойству присоединенной матрицы имеем:
Тогда
Раскрывая скобки в обеих частях равенства и присваивания коэффициенты при одинаковых , получим систему из n+1 равенства
Умножим первое равенство системы на Аn, второе – на Аn-1 и т.д., n-е равенство – на А, (n+1)-е равенство – на А0=Е:
При сложении этих равенств в левой части получим нулевую матрицу, а в правой части – выражение
Поэтому 
;
Линейная форма
Определение 2. Отображение F, заданное на евклидовом пространстве En в множество действительных чисел R, называют линейным функционалом векторного аргумента если для любых элементов 
и любого действительного числа 
выполняются соотношения:
(свойство аддитивности).
(свойство однородности).
Определение 3. Однородный многочлен 1-ой степени f(x)= 
относительно значений линейного функционала х1, х2, …, хn называется линейной формой.
Таким образом, любая линейная функция f(x) в n-мерном евклидовом пространстве является линейной формой относительно координат ее аргумента х.
Определение 4. Неоднородное уравнение линейной формы вида Ах1 + Вх2 = С, называется уравнением прямой в двумерном векторном пространстве R2, а неоднородное уравнение линейной формы вида Ах1 + Вх2 + Сх3 = D, называется уравнением плоскости в R3.
|
|
|
Теорема 35.1 Две системы линейных форм от n переменных будут эквивалентны по отношению к небособенным линейным преобразованиям, если ни один из обоих результатов не равен нулю.
Теорема 35.2 Единственными целыми рациональными инвариантами системы n линейных форм от n переменных будут постоянные кратные степеней результата.
Билинейный формы
Пусть есть векторное пространство над полем (чаще всего рассматриваются поля и).
Билинейной формой называется функция 
, линейная по каждому из аргументов:
, 
, 
, 
.
здесь 
и 
Свойства:
-Множество всех билинейных форм 
, заданных на произвольном фиксированном пространстве, является линейным пространством.
-Любую билинейную форму можно представить в виде суммы симметричной и кососимметричной форм.
-При выбранном базисе 
в L любая билинейная форма F однозначно определяется матрицей
-Это также означает, что билинейная форма полностью определяется своими значениями на векторах базиса.
-Размерность пространства 
есть 
.
-Несмотря на то, что матрица билинейной формы F зависит от выбора базиса, ранг матрицы билинейной формы в любом базисе один и тот же, он называется рангом билинейной формы F. Билинейная форма называется невырожденной, если ее ранг равен 
.
-Для любого подпространства 
ортогональное дополнение 
является подпространством 
.
- 
, где r — ранг билинейной формы F.
Квадратичные формы
Действительной квадратичной формой от n действительных переменных 
называют многочлен с действительными коэфициентами 
, каждый член которого имеют вторую степень, т.е. многочлен вида
Пусть 
– квадратичная форма . Коэффициент при 
в ней обозначен через 
, а коэффициент при произведении 
– через . Будем считать, что 
При такой договоренности квадратичную форму мажно записать следующим образом:
Такой вид записи квадратичной формы называют ее симметричным видом.
|
|
|
