 |
Теорема о размерности суммы и пересечения подпространств
|
|
|
|
Теорема 12.1 В конечномерным векторным пространстве Х рамерность суммы L1+L2 равна сумме размерностей этих подпространств минус размерность их пересечения, т.е.
dim(L1+L2) = dimL1 + dimL2 - dim(L1ÇL2).
Д-во:
В подпространстве L1ÇL2 выберем какой-либо базис 
эта система векторов линейно независима. Дополним ее до базиса в L1 системой векторов s w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 
и до базиса в L2 системой векторов s w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 
Объединяем систему 
= 
и докажем, что она является базисом в L1+L2
Через систему векторов 
линейно выражается любой вектор zÎ L1+L2. Действительно, для вектора z имеет z=х+у, где xÎ L1, уÎ L2. Вектор х линейно выражается через систему 
, а вектор у – через систему 
. Поэтому z линейно выражается через систему .
Докажем, что система векторов линейно независима.
(1)
Объединим слагаемые, относящиеся к векторам системе 
и 
:
Вектор а принадлежит L1. Но из равенства (1) следует, что
и вектор а принадлежит L2. Значит, аÎ L1ÇL2. Вектор а линейно выражается через систему e, т.е.
.
Можно рассматривать как разложение вектора аÎ L1 по базису .
В разложения по базису заключаем, что оба разложение совпадают, т.е. 
, 
С полученных равенство (1) примнимент вид
Поскольку система векторов линейно независима, это равенство возможно лишь нулевых значениях всех коэфициентов:
Доказано, система линейно независима и является базисом в подпространстве L1+L2.
, 
, 
, то
= 
= 
= 
. Теорема доказана.
Прямая сумма подпространств
Множество всех векторов х вида х = a+b, где aÎ L1, bÎ L2 называют суммой подпространств L1и L2 и обозначают L1+L2. Если при этом пересечение L1ÇL2 - нулевое подпространство, то сумму L1+L2 называют прямой суммой и обозначают через L1ÅL2.
|
|
|
Прямое дополнение подпространств
Если сумма L1+L2 подпространств L1и L2 в Х является прямой, то представление любого вектора х в виде х=a+b, где aÎ L1, bÎ L2 единственно. В частном случае, когда X = L1ÅL2, также каждый вектор х имеет единственное представление х=a+b, где aÎ L1, bÎ L2. Подпространства L1и L2 называют прямыми дополнениями друг друга, а слагаемое aÎ L1 – проекцией вектора х на подпространство L1 паралельно подпространству L2.
Критерий совместимости системы линейных уравнений
Пусть дана система линейных уравнений
с матрицей
А= 
и расширенной матрицей
B=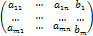 
Система называется совместимой, а если у системы решений нет, то несовместимой (противоречивой).
Теорема 15.1 (теорема Кронекера-Капелли)
Система линейных уравнений
совместна тогда и только тагда, когда ранг матрицы А системы равен рангу ее расширенной матрицы B.
Д-во:
Пусть система совместна. докажем, что rang(A) = rang(B).
Для этого возьмем какое-либо решение k1, k2, …,k n и подставие его в каждое уравнение системв.
Тогда
(1)
Эту систему перепишем в виде
Следовательно, при вычислении ранга матрицы В этот столбец в соответствии со свойством 6 ранга матрицы можно из матрицы B удалить. Это означает, что rang(A) = rang(B).
Пусть rang(A) = rang(B). Докажем, что система совместима. Равенство rang(A) = rang(B) означает, что базис системы столбцов матрицы А является и базисом системы столбцов матрицы В, т.е. существует набор таких чисел k1, k2, …,k n, что выполняется равенство (1). Это означает, что является решением рассматриваемой системы. Система совместна.
Теорема 15.2 Совместная система линейных уравнений эквивалентна любой своей базисной подсистеме.
|
|
|
