Размерность и свойства векторного пространства

 

Пусть V – конечномерное векторное пространство. Число n элементов произвольного базиса V называется размерностью V и обозначается dimV = n. В этом случае говорят, что V – n - мерное пространство. Нулевое пространство {0} будем считать нульмерным, т.е. dim{0} = 0.

Некоторые свойства векторных пространств:

1) Значение суммы комплексного числа векторов не зависит от порядка суммирования (например, x+y+z=(x+y)+z=x+(y+z)). Поэтому операцию сложения векторов можно распростронить на любое конечное число векторов.

2) Произведение нулевого вектора на любое число a из основного поля равно нулевому вектору, т.е. a×0=0. Действительно,

a×0=a×(0+0)=a×0+a×0. Следовательно,a×0=a×0-a×0=0.

3) Произведение любого вектора x на число 0 рано нулевому вектору,т.е. x×0. Действительно,x×0=x×(0+0)=x×0+x×0,откуда:

x×0=x×0-x×0=0.

4) Если αx=0,то либо α=0,либо х=0.В самом деле,если α ¹ 0, то

х =1х=[(1/α)×α]×х=(1/α)(αх)=(1/α)×0=0.

5) Для каждого вектора х противоположный вектор равен произведению х на число -1, т.е. –х= -1х. В самом деле,

х+(-1)х=1х+(-1)х=(1-1)х=0х=0. Означает, что вектор (-х) является противоположным к вектору х.

6) Для любого вектора х и любого числа α выполняется равенство α(-х)=(-αх).Действительно,

α(-х)= α[(-1)х]= [α(-1)]х= (-1)(αх) =(-αх).

7) Для любых векторов х и у и любого числа α выполняется равенство α(х-у)= αх- αу.В самом деле,

α(х-у)= α[х+(-у)]= αх+ α(-у)= αх- αу.

8) Для любого вектора х и любых чисел α,β выполняется равенство

(α- β)х= αх- βх, так как

(α −β)x=[α +(−β)]x=αx+(−β)x=αx−βx.

 

 

Координаты вектора

Пусть X – n -мерное векторное пространство над полем P, а система векторов - базис V. Мы считаем, что векторы в базисе упорядочены, т.е. перестановка векторов из базиса приводит к другому базису. Мы уже отмечали, что всякий

вектор xÎX однозначно представляется в виде линейной комбинации

векторов базиса: .

Коэффициенты этой линейной комбинации называются

координатами вектора x в базисе . Столбец будем называть координатным столбцом вектора x в базисе и обозначать [x]_A

Теорема 6.1. Пусть X – конечномерное векторное пространство и

– базис X. При сложении двух векторов из X их координаты складываются, при умножении вектора на число все его координаты умножаются на это число. Другими словами

Д-во

Пусть и

Тогда

 

Ранг системы векторов

Для того чтобы вычислить ранг системы векторов а₁, а₂, …,а _s в линейном арифметическом пространстве , из этих векторов, как из столбцов, следует записать матрицу и вычислить ранг.

 

Пример1.

Найти ранг системы векторов , ,

и выделить в ней максимальные линейно независимые подсистемы векторов.

Решение

Составим матрицу

Ее ранг равен двум. следовательно, ранг системы векторов также равен двум. При этом каждая пара этих векторов составляет максимальную линейно независимую подсистему, так как каждой паре векторов соответствует базисный минор. Наприиер, парам векторов и , и , и можно поставить в соответствие бизисные миноры

, , , расположенные в последних двух строках.

 

Ранг матрицы

Пусть дана матрица

Столбцы матрицы А будем расматривать как векторы линейного арифметического пространства К_m, а саму матрицу A – как конечную систему векторов.

Рангом матрицы называют ранг системы столбцов этой матрицы. Ранг матрицы обазначают через rang(A).

Если в матрице А выбраны какие-либо k строк и k столбцов, то определитель k-го порядка расположенных на пересечении выбранных строк и столбцов, называют минором k-го порядка матрицы А.

Некоторые свойства ранга матрицы.

1) При транспонировании матрицы ее ранг не изменяется.

2) При перестановке строк (столбцов) матрицы ее ранг не изменяется.

3) Ранг матрицы не изменяется при умножении всех элементов какой-либо строки (столбца) на нулевое число.

4) Ранг матрицы не изменится, если из нее удалить или в нее добавить строку (столбец). состоящую из нулей.

5) Ранг матрицы не изменится, если к одной ее строке (столбцу) приьавить другую строку (столбец), умноженную на некоторое число.

6) Ранг матрицы не изменяется, если из нее удалить или добавить строку (столбец), являющуюся линейной комбинацией других ее строк (столбцов).

Теорема 8.1 Если все миноры k-го порядка матрицы А равны нулю, то равны нулю все миноры более высокого порядка.

Д-во:

Пусть M – произвольный минор матрицы А порядка, большего k.

В соответствии с теоремой Лапласа, получим:

где M_i =миноры k-го порядка матрицы А. По условию теоремы такие миноры равны нулю. Поэтому равен нуля и минор М.Теорема доказано. Теорема доказана.

 

 

Теорема о ранге матрицы

 

Теорема 9.1 (теорема о ранге матрицы)

Ранг матрицы равен наивысшую порядку среди отличных от нуля ее миноров. Каждый столбец матрицы линейно выражается через ее столбцы, проходящие через какой-либо из таких миноров.

Д-во:

Пусть дана матрица А = () и пусть наивысший порядок среди ее ненулевых миноров равен r.

A =

Докажем. что столбцы, входящие в минор D, образуют линейно независимую подсистему в системе столбцов матрицы А. Для этого надо показать, что любой столбец матрицы А линейно выражается через столбцы а₁, а₂, …,а _r, входящие в минор D.

Выберем произвольный l-ый столбец.

При l £ r:

Пусть l > r. Выбираем произвольную i-ю строку, 1 £ i £ m, и ставим определитель

Если i £ r, то в определителье две одинаковые строки и он равен нулю. Если же i > r, то этот определитель есть минор (r+1)-го порядка матрицы А и поэтому равен нулю.

Таким обрзом, определитель нулевой при любом i.

Получим: (1)

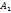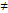где , …, – алгебраические дополнения элементов последней строки определителя , причем = D 0

Из равенства (1) находим:

, i = 1,2,…,m

Данное равенство означает, что l-ый столбец матрицы А линейно выражается через столбцы, входящие в минор D. Таким образом, теорема доказана.

Теорема 9.2 Ранг произведения нескольких матриц не превышает рангов матриц каждого из сомножителей.

Теорема 9.3 Если А – если матрица размера m´n, Q₁ и Q₂ – квадратные невырожденные матрицы порядков m и n, то

rang(Q₁A) = rang(АQ₂) = rang(A).

Д-во:

Согласно теореме 9.3 для произведения C = C имеем:

rang(C) £ rang(A) и в то же время, по скольку А = C, заключаем, что

rang(А) £ rang(С). Из полученных неравенств вытекает равенство rang(C) = rang(A). Теорема доказана.

 

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: