 |
Ограничение билинейных и квадратичных форм
|
|
|
|
Ортагональные вектора
Пусть L – подпространство евклидова пространства Е. Каждый вектор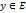 
может быть единственным способом представлен в виде 
, где 
, а вектор 
ортогонален вектору из L, т.е. 
. Вектор 
называют ортогональной проекцией вектора 
на пространство L и обозначают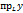 
, а вектор называют ортогональной составляющей вектора .
Очевидно, что если 
, то 
, и, наоборот, если , то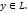 
Длина ортогональной составляющейвектора х меньше длины любого вектора, опущенного из конца вектора х на подпространство L.
Действительно, пусть – произвольный вектор, опущенный из конца вектора х на подпространство L и 
- ортогональная составляющая вектора х. Тогда 
при 
Поэтому 
так как 
и ортогональны.
Приведение к кононическому виду
Теорема 39.1 Любую квадратичную форму с помощью невырожденного линейного преобразования переменных можно привести к каноническому виду.
Привести квадратичную форму к каноническому можно методом Лагранжа.
Пусть, например, в квадратичной форме 
есть член с квадратом переменной 
, т.е. 
. Тогда получим
где 
– квадратичная форма уже только от переменных 
Введем новые переменные
И примет вид
Пусть Q – его матрица, А – матрица квадратичной формы, С – диагональная матрица полученного канонического виде. Тогда формула примет вид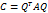 
Алгоритм Логранжа
Нормальный вид квадратичной формы над C и R
Пусть квадратмичная форма 
приведена к каноническому виду 
, 
, 
Выполним дополнительное преобразование переменных
,
В результате квадратичная фр=орма преобразуется к виду.
такой вид квадратичной формы называют ее нормальным видом
Закон инерции вещественных квадратичных форм
|
|
|
Квадраты переменных, входящие в канонический вмд с положительными коэфициентами, будем называть положительными квадратами, а квадратв, входящие в канонический вид с отрицательными коэфициентами, - отрицательными квадратами.
Для квадратичных форм имеет место следующий закон инерции.
Теорема 43.1 Число положительных квадратов, как и число отрицательных квадратов, в любом каноническом виде данной квадратичной формы одно и то же и не зависит от того, каким невырожденным линейным преобразованием переменных получен канонический вид.
Д-во:
Пусть квадратичная форма 
имеет канонический вид
, в базисе 
и канонический вид 
в базисе 
Общее количество квадратов в двух канонических видах одинаково и совпадает с рангом квадратичной формы.
Допустим, r > p. Рассмотрим в линейном пространстве подпространства 
и 
. Поскольку r > p, то сумма размерностей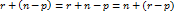 
этих подпространств перевышает размерность n рассматриваемого линейного пространства. Поэтому т.е. 
.
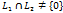Из условия 
вытекает представление
а из условия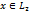 
– представление
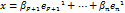
Значит вектор х в базисе 
пространства X имеет столбец координат 
, а в базисе – столбец координат 
.
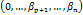Из первого получаем 
а из второго - 
Полученное противоречие показывает, что r > p неверно. Следовательно, r = p и количесиво квадратов одного знака в двух канонических видах данной квадратичной формы совпадают.
Знакоопределенная форма
Квадратичную форму 
называют положительно (отрицательно) определенной, если
) при 
Если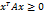 
) при , то ее называют положительно (отрицательно) полуопределенной
Квадратичную форму, принимающую как положительные, так и отрицательные значения, называют знакопеременной
Для того чтобы квадратичная форма от nпеременных была положительно (отрицательно) определенной, необходимо и достаточно, чтобы она приводилась к каноническому виду с n положительными (отрицательными) квадратами.
|
|
|
Критерий Сильвестра
Для того чтобы квадратичная форма от n переменных была положительно определенной, необходимо и достаточно, чтобы все угловые миноры ее матрицы А были положительными, т.е.
…
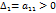
Для того чтобы квадратичная форма была отрицательно определенной, необходимо и достаточно, чтобы знаки угловых миноров матрицы А квадратичной формы чередовались, начиная со знака минус.
|
|
|
