Сигма (s) и коэффициент вариации (Сv). Их значение и применение.

Характеристика разнообразия признака в статистической совокупности.

Величина признака может быть не одинакова у всех членов совокупности, несмотря на ее относительную однородность. Статистика позволяет определить уровень разнообразия признака в изучаемой совокупности или, то на сколько разнятся (колеблются) показатели этого признака у разных единиц наблюдения, для этого были разработаны:

Критерии разнообразия признака

1. Лимит (Lim) – определяется крайними значениями вариант в вариационном ряду.

2. Амплитуда (Am) – разность крайних величин вариант.

3. Среднее квадратическое отклонение (s) – дает наиболее полную характеристику разнообразия признака в совокупности.

Способы расчета среднеквадратического отклонения:

1. Среднеарифметический способ. (используется при числе наблюдений

≤ 30 или р=1)

2. Расчет (s) по способу моментов (если n ≥ 30)

В медицине его частое применение можно видеть в определении пределов нормы и патологии: С помощью (s) можно проводить диагностику тяжести заболевания и дифференциальную диагностику.

4. Коофицент вариации (С_v) – относительная мера разнообразия, позволяет определить степень разнообразия признака: Используется при сравнении разноименных или разноразмерных признаков. Например при сравнении роста, веса, окружности головы у детей разных возрастов В этом случае необходимо ориентироваться не на среднее квадратическое отклонение, а на коофицент вариации (С_v) или коофицент разнообразия. С_{v = %} Также с помощью (С_v) можно произвести оценку степени разнообразия признака. Оценка степени разнообразия признака Если: (С_v) >20% - сильное разнообразие признака. (С_v) = 20% - 10% - среднее разнообразие признака. (С_v) < 10% - слабоеразнообразие признака. При оценке степени разнообразия (С_v) позволяет выявить наиболее и наименее устойчивые признаки в совокупности. Например: при сравнении роста, веса, возраста пациентов можно установить по какому признаку они больше всего отличаются друг от друга или напротив более схожи, т.е. какие признаки наиболее устойчивы и постоянны в данной совокупности.

13. Статистическая оценка достоверности результатов исследования. Применение критерия «t». Доверительные границы средних и относительных величин.

Достоверность статистических показателей – это степень соответствия отображаемой ими действительности. Достоверными результатами считаются те, которые не искажают и правильно отражают объективную реальность. Оценка достоверности необходима для определения с какой вероятностью можно перенести результаты исследования с выборочной совокупности на генеральную совокупность.

Для оценки достоверности необходимо:

1. Оценить ошибку репрезентативности среднеарифметических (т_м) и относительных величин (т_р).

2. Определить доверительные границы средних и относительных величин.

3. Оценить достоверность разности между двумя интенсивными показателями и средними величинами.

4. Оценить данные и сформулировать вывод.

Определение доверительных границ М и Р. Доверительные границы - это границы средних или относительных величин вероятность выхода за пределы, которых незначительна. Этот метод применяется тогда, когда приходится по результатам выборочной совокупности судить о явлении во всей генеральной совокупности. Условие применения метода:

1. Обязательное условие при использовании этого метода – это репрезентативность выборочной совокупности.

2. Для переноса результатов выборочной совокупности на генеральную нужно определить степень вероятности безошибочного прогноза (Р).

(Р) показывает в каком % случаев результаты выборочной совокупности будут характерны для генеральной. Для этого используется (t) – критерий достоверности (точности), размер доверительного интервала. Критерий достоверности (t) выбирает сам исследователь, руководствуясь простым правилом. При п > 30:(t) = 2 à (Р) = 95,5%(t) = 3 à (Р) = 99,7%

NB! Для большинства медико-биологических исследований считается достаточной степень вероятности безошибочного прогноза (Р) = 95,5%, т.е. число случаев генеральной совокупности, в которых могут наблюдаться отклонения от выявленной закономерности составит 4.5%.Для особо сложных исследований, при которых отклонения от нормы чреваты гибелью пациента, применяется (Р) = 99,7%, т.е. отклонение от ожидаемого результата должно составить не более 0,3% случаев. При п < 30: (t) определяют по специальным таблицам.

Доверительные границы средних величин

Доверительные границы относительных величин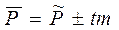

Доверительные границы зависят от размера доверительного интервала (критерия точности) и ошибки репрезентативности. Если ошибка большая, то получают большие доверительные границы для выборочной совокупности, которые могут противоречить генеральной совокупности, в отдельных случаях даже превышать ее. Это свидетельствует о недостаточности единиц наблюдения или о нерепрезентативности выборочной совокупности. Стандартный Вывод: С вероятностью безошибочного прогноза 95,5% можно утверждать, что достоверные границы (исследуемого признака), при переносе результатов исследования на всю генеральную совокупность будут не менее % … и не более…%.

Оценка достоверности разности результатов исследования. Этот метод применяется при сравнении двух исследуемых групп, когда нужно определить, случайны или закономерны, т.е. обусловлены какой либо причиной, различия между средними величинами или относительными показателями. При его использовании обязательными условиями являются: репрезентативность выборочной совокупности, наличие причинно-следственной связи между сравниваемыми величинами. Для средних величин: t = Для относительных показателей: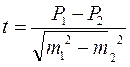

Если (t)≥2, что соответствует вероятности безошибочного прогноза (Р)≥95,5%, поэтому разность следует считать достоверной, т.е. существенной или обусловленной влиянием какого-то фактора, что будут верно, и для генеральной совокупности.

При (t)<2, вероятность безошибочного прогноза составит (Р)<95,5%, следовательно разность в показателях случайна, т.е не обусловлена какой-то закономерностью. Из формул следует, что оценка достоверности разности результатов исследования будут зависеть от ошибки репрезентативности, которая в свою очередь зависит о числа единиц наблюдения. Вывод: С вероятностью безошибочного прогноза 95,5% можно утверждать, что показатель 1(его характеристики) достоверно выше 2 показателя (его характеристики), следовательно признак X влияет на признакY.