Уравнения Лагранжа II-го рода

Применение методов аналитиЧеской Механики к анализу движениЯ механиЧеских систем

Основу аналитической механики составляют общие принципы, из которых аналитическим путем могут быть получены основные дифференциальные уравнения движения или условия равновесия механической системы.

В данном разделе курсовой работы требуется:

- составить дифференциальные уравнения движения системы (желательно несколькими способами);

- найти решения дифференциальных уравнений движения (в большинстве случаев численными методами);

- построить графики изменения координат и скоростей на заданном интервале времени;

- произвести анализ движения системы, варьируя начальные условия и параметры системы;

- решить другие задачи, которые могут быть поставлены преподавателем индивидуально.

 

Связи и виртуальные перемещения

Пусть имеется система, состоящая из N материальных точек Если на положения и скорости точек наложены ограничения геометрического или кинематического характера (механические связи), то такая система называется несвободной. Для свободных систем связи отсутствуют.

Если скорости точек не входят в уравнения связей, то такие связи называются конечными или геометрическими. Ограничения, накладываемые на движение системы такой связью, могут быть описаны уравнением

, (3.1)

где - радиусы-векторы точек ,

t - время.

Связь, описываемая уравнением

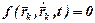, (3.2)

называется кинематической. Если она путем интегрирования не может быть приведена к виду (3.1), то ее называют неголономной или дифференциальной.

Связь называется стационарной, если время явно не входит в уравнение связи

(3.3)

и нестационарной, если параметр t присутствует, например, (3.1).

Система называется склерономной, если на нее наложены только стационарные связи. В противном случае система называется реономной.

Связи, которые записываются в виде равенства (например, (3.1)), называются удерживающими, а которые в виде неравенства - неудерживающими

.

Пусть на материальную систему наложены d конечных связей

(3.4)

и g линейных дифференциальных связей

, (3.5)

где - вектор и скаляр, представляющие собой заданные функции от t и .

Продифференцируем уравнения конечных связей (3.4)

(3.6)

Систему векторов будем называть возможными скоростями для некоторого времени t и для некоторого возможного в этот момент положения системы, если векторы удовлетворяют d+g линейным уравнениям (3.5) и (3.6).

Для каждого возможного положения системы в момент времени t существует бесчисленное множество систем возможных скоростей.

Систему бесконечно малых перемещений будем называть возможными перемещениями.

Умножив уравнения (3.5) и (3.6) на dt, получим уравнения, определяющие возможные перемещения

(3.7)

Возьмем две системы возможных перемещений для одного и того же момента времени и для одного и того же положения системы:

и .

Как , так и , удовлетворяют системе (3.7), а их разности

(3.8)

удовлетворяют соотношениям:

(3.9)

Векторы , удовлетворяющие соотношениям (3.9) называются виртуальными перемещениями. Сравнивая выражения (3.7) и (3.9) можно заключить, что виртуальные перемещения совпадают с возможными перемещениями при “замороженных” связях.

Можно еще сказать, что виртуальные перемещения представляют собой перемещения точек системы из одного возможного положения системы в момент времени t в другое бесконечно близкое, возможное для того же самого момента времени t, положение системы.

При стационарных связях виртуальные перемещения совпадают с возможными.

 

Общее уравнение динамики

Общее уравнение динамики имеет вид:

(3.10)

где -активные силы, приложенные к системе;

-масса k -ой точки;

-ускорение k -ой точки;

-виртуальное перемещение k -ой точки.

Уравнение (3.10) показывает, что в любой фиксированный момент времени сумма элементарных работ активных сил и сил инерции на любых виртуальных перемещениях равна нулю при условии, что на систему наложены идеальные и удерживающие связи.

Важным свойством общего уравнения динамики является то, что оно не содержит реакций идеальных связей. Иногда это уравнение можно использовать для исследования движения механических систем и в тех случаях, когда не все связи являются идеальными, например, когда имеются связи с трением. Для этого следует к активным силам добавить те составляющие реакций, которые обусловлены наличием сил трения.

Вычисление суммы работ сил инерции на виртуальных перемещениях твердого тела проводится по следующим формулам.

1. При поступательном движении тела:

где -главный вектор сил инерции тела (M - масса тела, - ускорение центра масс),

- виртуальное перемещение центра масс тела.

2. При вращении тела вокруг неподвижной оси:

где -главный момент сил инерции тела относительно оси вращения ( - момент инерции тела относительно оси вращения, e - угловое ускорение тела),

- виртуальное угловое перемещение тела.

3. При плоско - параллельном движении:

где - главный момент сил инерции тела относительно оси, проходящей через центр масс С тела.

Частным случаем общего уравнения динамики является принцип виртуальных перемещений (общее уравнение статики). Действительно, в том случае, когда механическая система находится в покое, все силы инерции равны нулю, и из общего уравнения динамики вытекает принцип виртуальных перемещений: для того чтобы механическая система, на которую наложены идеальные связи находилась в равновесии, необходимо и достаточно, чтобы сумма элементарных работ всех активных сил, приложенных к рассматриваемой системе, на любом из ее виртуальных перемещений была равна нулю

(3.11)

Рассмотрим процедуру использования уравнения (3.10) для составления дифференциальных уравнений движения систем с двумя степенями свободы:

1. Изобразить механическую систему в произвольный момент времени.

2. Показать на рисунке активные силы и моменты, а также силы и моменты, соответствующие неидеальным связям (например, силы трения).

3. Определить главные векторы и главные моменты сил инерции.

4. Выбрать обобщенные координаты в числе, равном числу степеней свободы системы.

5. Дать виртуальное перемещение, соответствующее одной из степеней свободы системы, считая при этом виртуальные перемещения, соответствующие остальным степеням свободы, равными нулю.

6. Вычислить сумму элементарных работ всех сил и моментов (см. п. 2 и 3) на соответствующих виртуальных перемещениях и приравнять эту сумму нулю.

7. Повторить п. 4 - 6 для каждого независимого движения системы.

При применении общего уравнения динамики к системам с двумя и большим числом степеней свободы, в связи с громоздкостью выкладок, можно использовать следующие рекомендации:

1. Сделать предположение о направлении ускорений точек системы.

2. Направить на рисунке силы инерции в стороны, противоположные выбранным направлениям соответствующих ускорений.

3. Определить знаки элементарных работ сил инерции в соответствии с их направлениями на рисунке и избранными направлениями виртуальных перемещений точек системы.

4. Если искомые ускорения оказываются положительными, то сделанные предположения о направлениях ускорений подтверждаются, если отрицательными, то соответствующие ускорения направлены в другую сторону.

Уравнения Лагранжа II-го рода

 

Уравнения Лагранжа II-го рода являются одним из наиболее удобных приемов составления уравнений движения механических систем. Они имеют вид

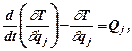j=1,2,...,s; (3.12)

где T - кинетическая энергия механической системы,

-обобщенные координаты, скорости и силы, соответственно,

s- число степеней свободы механической системы.

Уравнения (3.12) образуют систему s уравнений второго порядка относительно s функций . Порядок системы (3.12) равен 2 s. Форма уравнений Лагранжа не зависит от выбора обобщенных координат От выбора обобщенных координат зависит вид функции только T и . В связи с этим говорят, что уравнения Лагранжа II-го рода обладают свойством инвариантности.

Уравнения движения с помощью уравнений Лагранжа составляются следующим образом:

1. Определяется число степеней свободы механической системы.

2. Выбираются обобщенные координаты, однозначно и наиболее удобным образом определяющие положение всех тел в системе. Для голономных систем число обобщенных координат равно числу степеней свободы.

3. Кинетическая энергия системы выражается через обобщенные координаты и производные от них по времени - обобщенные скорости .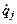

4. Находятся обобщенные силы , соответствующие выбранным обобщенным координатам .

5. Вычисляются производные от кинетической энергии согласно уравнениям (3.12) и составляются уравнения движения.

При определения кинетической энергии необходимо учитывать следующее.

1. Для вычислении кинетической энергии тел, входящих в систему, в соответствующие расчетные формулы подставляются абсолютные скорости (линейные и угловые), которые будут складываться из переносных и относительных.

2. Если все обобщенные координаты независимы друг от друга, то для определения отдельных скоростей можно сначала определить те скорости, которые будут иметь точки и тела при отличии от нуля только одной из обобщенных координат (частные скорости), а затем сложить их

где - вектор скорости k -ой точки,

- скорость, которую будет иметь k -ая точка, если будет отлична от нуля только одна обобщенная скорость .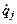

Аналогичное соотношение можно записать для угловых скоростей:

или, если движение происходит в одной плоскости:

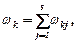
Для определения обобщенных сил используют три способа.

1.Используется в тех случаях, когда известны аналитические зависимости проекций всех активных сил на оси неподвижной системы координат от обобщенных координат. Тогда

 

 

2.При определении обобщенных сил пользуются тем, что обобщенные координаты и их вариации являются независимыми. Поэтому при определении возможной работы можно рассмотреть такое возможное перемещение системы, при котором будет изменяться только одна обобщенная координата . Тогда для всех i, кроме i =j, и из выражения (3.4) получаем

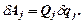
Откуда

Повторяя рассмотренную процедуру для всех обобщенных координат j = 1...s, получают все обобщенные силы.

3. Позволяет определять обобщенные силы в консервативных механических системах. В них следует вычислить потенциальную энергию П, которая зависит только от обобщенных координат, а затем найти все обобщенные силы по следующей формуле

В заключении заметим, что в уравнениях Лагранжа II-го рода не содержаться реакции идеальных связей. Если же нужно найти реакции связей, то надо после интегрирования уравнений Лагранжа подставить функции в выражение

где -радиус-векторы точек системы относительно начала инерциальной системы координат.

Тогда равнодействующие реакций связей, приложенных к точкам системы, найдутся из соотношений

Пример составления

123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: