 |
Условия равновесия механических систем
|
|
|
|
Согласно принципу возможных перемещений (основному уравнению статики), для того, чтобы механическая система, на которую наложены идеальные, стационарные, удерживающие и голономные связи, находилась в равновесии, необходимо и достаточно, чтобы в этой системе были равны нулю все обобщенные силы:
(5.1)
где Qj - обобщенная сила, соответствующая j - ой обобщенной координате;
s - число обобщенных координат в механической системе.
Если для исследуемой системы были составлены дифференциальные уравнения движения в форме уравнений Лагранжа II - го рода, то для определения возможных положений равновесия достаточно приравнять обобщенные силы нулю и решить полученные уравнения относительно обобщенных координат.
Если механическая система находится в равновесии в потенциальном силовом поле, то из уравнений (5.1) получаем следующие условия равновесия:
(5.2)
Следовательно, в положении равновесия потенциальная энергия имеет экстремальное значение. Не всякое равновесие, определяемое вышеприведенными формулами, может быть реализовано практически. В зависимости от поведения системы при отклонении от положения равновесия говорят об устойчивости или неустойчивости данного положения.
Устойчивость равновесия
Определение понятия устойчивости положения равновесия было дано в конце XIX века в работах русского ученого А. М. Ляпунова [4, 5]. Рассмотрим это определение.
Для упрощения выкладок условимся в дальнейшем обобщенные координаты q1, q2,..., qs отсчитывать от положения равновесия системы:
, где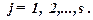 
Положение равновесия называется устойчивым, если для любого сколь угодно малого числа e > 0 можно найти такое другое число d(e) > 0, что в том случае, когда начальные значения обобщенных координат и скоростей не будут превышать d:
|
|
|
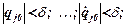
значения обобщенных координат и скоростей при дальнейшем движении системы не превысят e
.
Иными словами, положение равновесия системы q1 = q2 =...= qs = 0 называется устойчивым, если всегда можно найти такие достаточно малые начальные значения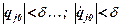 
, при которых движение системы 
не будет выходить из любой заданной сколь угодно малой окрестности положения равновесия 
. Для системы с одной степенью свободы устойчивое движение системы можно наглядно изобразить в фазовой плоскости (рис. 5.1). Для устойчивого положения равновесия движение изображающей точки, начинающееся в области [- d, d ], не будет в дальнейшем выходить за пределы области [- e, e ].
 |
Рис. 5.1
Положение равновесия называется асимптотически устойчивым, если с течением времени система будет приближаться к положению равновесия, то есть
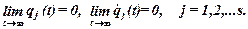
Определение условий устойчивости положения равновесия представляет собой достаточно сложную задачу [ 4 ], поэтому ограничимся простейшим случаем: исследованием устойчивости равновесия консервативных систем.
Достаточные условия устойчивости положений равновесия для таких систем определяются теоремой Лагранжа - Дирихле: положение равновесия консервативной механической системы устойчиво, если в положении равновесия потенциальная энергия системы имеет изолированный минимум.
Потенциальная энергия механической системы определяется с точностью до постоянной. Выберем эту постоянную так, чтобы в положении равновесия потенциальная энергия равнялась нулю:
П(0)= 0.
Тогда для системы с одной степенью свободы достаточным условием существования изолированного минимума, наряду с необходимым условием (5.2), будет условие
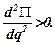
Так как в положении равновесия потенциальная энергия имеет изолированный минимум и П(0) = 0, то в некоторой конечной окрестности этого положения
|
|
|
П(q) > 0.
Функции, имеющие постоянный знак и равные нулю только при нулевых значениях всех своих аргументов, называются знакоопределенными. Следовательно, для того, чтобы положение равновесия механической системы было устойчивым необходимо и достаточно, чтобы в окрестности этого положения потенциальная энергия была положительно определенной функцией обобщенных координат.
Для линейных систем и для систем, которые можно свести к линейным при малых отклонениях от положения равновесия (линеаризовать), потенциальную энергию можно представить в виде квадратичной формы обобщенных координат [ 2, 3, 9 ]
(5.3)
где 
- обобщенные коэффициенты жесткости.
Обобщенные коэффициенты являются постоянными числами, которые могут быть определены непосредственно из разложения потенциальной энергии в ряд или по значениям вторых производных от потенциальной энергии по обобщенным координатам в положении равновесия:
(5.4)
Из формулы (5.4) следует, что обобщенные коэффициенты жесткости симметричны относительно индексов
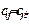
Для того, чтобы выполнялись достаточные условия устойчивости положения равновесия, потенциальная энергия должна быть положительно определенной квадратичной формой своих обобщенных координат.
В математике существует критерий Сильвестра, дающий необходимые и достаточные условия положительной определенности квадратичных форм: квадратичная форма (5.3) будет положительно определенной, если определитель, составленный из ее коэффициентов, и все его главные диагональные миноры будут положительными, т.е. если коэффициенты cij будут удовлетворять условиям
D1 = c11 > 0,
D2 = 
> 0,
.....
Ds = 
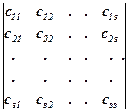> 0,
В частности, для линейной системы с двумя степенями свободы потенциальная энергия и условия критерия Сильвестра будут иметь вид
П = 
(
),
Аналогичным образом можно провести исследование положений относительного равновесия, если вместо потенциальной энергии ввести в рассмотрение потенциальную энергию приведенной системы [ 4 ].
|
|
|
