 |
Уравнений движения системы с двумя степенями свободы.
|
|
|
|
Рассмотрим механическую систему, которая состоит из стержня CD длиной l1 и массой mcт, трубки KN длиной 2 l и массой mтр, шарика M массой mш, прикрепленного к пружине жесткостью c (рис.3.1). Трубка имеет возможность вращаться вокруг горизонтальной оси AB. В начальный момент система находилась в покое, шарик имел координату y0 (при этом пружина была не деформирована).
Рис. 3.1.
Требуется:
-составить дифференциальные уравнения движения системы (двумя методами);
-проинтегрировать полученные уравнения;
-построить графики изменения обобщенных координат и обобщенных скоростей.
Дифференциальные уравнения движения можно системы составить с помощью общего уравнения динамики или уравнений Лагранжа II-го рода. Полученные уравнения следует сравнить с уравнениями движения, полученными в других разделах работы.
 |
Присоставления уравнений движения с помощью общего уравнения динамики учитываются активные силы и силы инерции (рис.3.2):
Рис. 3.2 -Активные силы и силы инерции
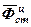- центробежная сила инерции стержня;
- вращательная сила инерции стержня;
- момент сил инерции стержня;
- центробежная сила инерции трубки;
- вращательная сила инерции трубки;
- момент сил инерции трубки;
- переносная центробежная сила инерции шарика; 
- переносная вращательная сила инерции шарика;
- сила инерции шарика в относительном движении.
- кориолисова сила инерции Кориолиса шарика.
Силы инерции трубки и стержня приложены в центрах масс этих тел.
Найдем величины сил и моментов инерции:
В качестве обобщенных координат выбираем угол поворота стержня j и координату y, определяющую положение шарика в трубке.
Выведем первое дифференциальное уравнение движения системы. Для этого фиксируем координату y, даем системе виртуальное перемещение dj, находим элементарную работу, которую могут совершить все активные силы и силы инерции, и приравниваем ее нулю
|
|
|
Подставим в это уравнение величины сил и моментов инерции и разделим все слагаемые на общий множитель dj
(3.13)
Получим второе дифференциальное уравнение движения системы. Для этого фиксируем координату j, даем виртуальное перемещение dy, находим элементарную работу, приравниваем ее нулю
Значение угла a зависит от положения шарика в трубке (рис. 3.2)
.
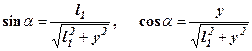С учетом этих соотношений получим
или
(3.14)
Уравнения (3.13) и (3.14) представляют собой систему дифференциальных уравнений, описывающих движение рассматриваемой механической системы.
Составим уравнения движения с помощью уравнений Лагранжа II- рода. В выбранных обобщенных координатах j и y онипринимают вид:
(3.15)
(3.16)
где T - кинетическая энергия системы;
- обобщенные силы, соответствующие обобщенным координатам j и y.
Найдем кинетическую энергию системы. Она состоит из кинетических энергий всех тел, входящих в систему: стержня Tст , трубки Tтр и шарика Tш
T=Tст + Tтр + Tш, (3.17)
где
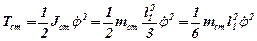(3.18)
(3.19)
.
Абсолютная скорость шарика 
равна геометрической сумме относительной и переносной скоростей (рис.3.3),
Рис. 3.3.
ее величина определяется по формуле
(3.20)
где 
- относительная и переносная скорости шарика.
(3.21)
Подставив выражения (3.21) и значение sina в уравнение (3.20), получим
. (3.22)
Тогда для кинетической энергии системы получим
. (3.23)
Найдем все производные левой части уравнений (3.15) и (3.16)
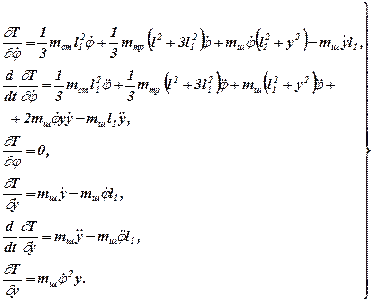(3.24)
Обобщенные силы можно определить двумя способами.
1. Фиксируем координату y, даем виртуальное перемещение dj, находим элементарную работу
откуда
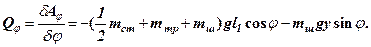(3.25)
Фиксируем координату j, даем виртуальное перемещение dy, находим элементарную работу
где 
- сила упругости пружины.
|
|
|
Тогда
. (3.26)
2.Вычислим потенциальную энергию системы П
Здесь Пст, Птр, Пш, Пупр - потенциальная энергия сил тяжести стержня, трубки, шарика, а также силы упругости пружины, которые определяются формулами
Тогда потенциальная энергия системы примет вид
Найдем обобщенные силы:
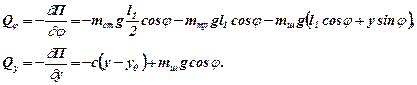
Подставив производные (3.24) и обобщенные силы Qj и Qy в уравнения (3.15) и (3.16), получим дифференциальные уравнения движения системы
Эти дифференциальные уравнения совпадают с уравнениями движения (3.13) и (3.14), полученными с помощью общего уравнения динамики.
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ
|
|
|
