 |
Оптимальный уровень запасов
|
|
|
|
Фирмы имеют возможность стимулировать продажи, поддерживая большие запасы, но при этом растут соответствующие затраты. Задача финансового менеджера – определить, какой уровень запасов обеспечивает фирме наибольшую прибыль. И в первую очередь требуется оценить затраты, которые ассоциируются с запасами.
Различают два вида затрат: текущие затраты и затраты на заказ.
Текущие затраты вызваны операциями по хранению запасов: арендой складских помещений, страхованием, обеспечением сохранности и т.д. Обычно они выражены удельной величиной. Например, хранение на складе 1 тонны металла составляет столько-то рублей в год.
Если предположить, что текущие затраты на единицу запасов есть постоянная величина, тогда
текущие затраты = 
· C,
где – средняя величина запаса; C – удельные текущие затраты.
Затраты на заказ. Они возникают всякий раз, когда размещается заказ на поставку какого-либо сырья или материалов (а также покупных изделий и полуфабрикатов) и могут быть канцелярскими и телефонными
расходами, оплатой труда сотрудников отдела снабжения и т. д. Эти затраты можно отнести к постоянным, не зависящим от величины заказа. Обычно они выражаются в стоимостной форме на один заказ (например, 500 руб. на заказ).
Если свести роль финансового менеджера к минимизации двух видов затрат, то это сильно упрощает проблему, так как тенденции их изменения противоположны. Так, рост уровня запасов вызывает рост текущих затрат, снижая при этом затраты на заказ, поскольку количество этих заказов уменьшается.
Фирмы, не имеющие запасов, сводят текущие затраты к нулю, но им надо делать заказы на материалы всякий раз, когда эти материалы необходимы для осуществления производства. Тем самым они максимизируют затраты на заказ. И наоборот, фирма может минимизировать затраты на заказ, сделав всего один заказ на все материалы сразу, но при этом ее текущие затраты, вызванные содержанием огромных запасов, будут очень высоки.
|
|
|
Проблема может быть решена при условии, если большие объемы запасов способствуют росту продаж. Известно, что чем больше товарных запасов демонстрируется, тем больше вероятность найти своего покупателя. Но чем больше запасов готовой продукции, не выставленной для обозрения потенциальными покупателями, тем меньше товаров может быть продано из-за отсутствия, к примеру, нужного размера или модели. Однако не факт, что тот уровень запасов, который обеспечивает большую выручку и меньшие затраты, является оптимальным.
Чтобы определить оптимальную величину, необходимо найти баланс между затратами и прибылью при различных уровнях запасов.
Поскольку затраты на заказ есть постоянная величина, ее определяют по формуле
затраты на заказ = 
,
где S – общее потребление запасов (потребность); Q – величина заказа;
P – затраты на выполнение одного заказа.
Между двумя видами затрат существует обратная зависимость: чем больше величина заказа, тем выше текущие затраты, но ниже затраты на заказ. Следовательно, надо найти такую величину заказа, при котором суммарные затраты будут минимальными. Это и будет оптимальная величина заказа.
Этой теме посвящена целая отрасль в области исследования операций. Ученые разработали ряд моделей, среди которых наибольшую популярность получила модель экономически обоснованного размера заказа. При определенных, достаточно разумных допущениях эта модель использует формулу:
= 
.
Допущения: уровень использования запасов постоянный; время выполнения каждого заказа согласовано; дата поставки совпадает с точкой, когда уровень запасов достигает нуля. Это не относится к проблеме дефицита, имеющей место, когда у фирмы закончился запас какого-то наименования и нет возможности его купить или поставить. Ослабление данных допущений не вызывает значительных изменений в расчетах.
|
|
|
Экономичный размер заказа (EOQ) – это количество (объем, размер), которое наиболее выгодно заказывать. Рассчитаем данную величину, переведем ее в средний уровень запасов и определим минимальную сумму общих затрат (текущих и на заказ) на следующем примере.
Ежемесячная потребность в комплектующих деталях составляет 500 шт. по цене 100 руб. Затраты, связанные с оформлением и получением заказа, составляют 300 руб. Текущие затраты на содержание одной комплектующей детали составляют 30 % ее цены. Требуется определить, какое количество деталей надо заказывать единовременно:
= 
= 100 шт.
Оптимальный размер заказа – 100 шт. комплектующих деталей. Учитывая допущения, можно определить, что средний размер запасов равен 50 шт. (EOQ / 2).
В течение каждого месяца заказ надо повторять 5 раз (500: 100), т.е. через каждые 6 дней (30: 5).
Можно также рассчитать величину затрат:
текущие затраты = среднемесячная величина запасов в шт. · удельныетекущие затраты =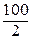 
· 30 = 1 500 руб.;
затраты на заказ за месяц = 
· 300 = 1 500 руб.
Всего затрат на содержание запаса: 1 500 + 1 500 = 3 000 руб.
Это минимальные затраты на содержание запасов, которые обусловлены заказом в 100 шт., повторяющимся 5 раз в течение месяца. Всякий другой размер заказа будет иметь большие затраты.
Более подробно и полно модель EOQ рассматривается в курсах производственного менеджмента и логистики.
|
|
|
