 |
Лекция 14. Элементы неравновесной термодинамики
|
|
|
|
Лекция 14. Элементы неравновесной термодинамики
Термодинамика неравновесных процессов. Закон сохранения массы в термодинамике неравновесных процессов. Закон сохранения импульса в термодинамике неравновесных процессов. Закон сохранения энергии в термодинамике неравновесных процессов. Уравнение баланса энтропии.
14. 1. Термодинамика неравновесных процессов
В термодинамике неравновесных процессов системы рассматриваются как непрерывные среды, а их параметры состояния - как полевые переменные, т. е. непрерывные функции координат и времени. Для макроскопического описания неравновесных процессов применяют следующий метод: систему представляют состоящей из элементарных объёмов (элементов среды), которые всё же настолько велики, что содержат очень большое число частиц. Состояние каждого выделенного элемента среды характеризуется температурой, давлением и др. термодинамическими параметрами, зависящими от координат и времени. Количественное описание неравновесных процессов при таком методе заключается в составлении уравнений баланса для элементарных объемов на основе законов сохранения массы, импульса и энергии, а также уравнения баланса энтропии и феноменологических уравнений рассматриваемых процессов, выражающих потоки массы, импульса и энергии через градиенты термодинамических параметров. Методы термодинамики необратимых процессов позволяют:
а) сформулировать для неравновесных процессов 1-е и 2-е начала термодинамики в локальной форме (зависящей от положения элемента среды);
б) получить из общих принципов, не рассматривая деталей взаимодействия частиц, полную систему уравнений переноса, т. е. уравнения гидродинамики, теплопроводности и диффузии для простых и сложных систем (с химическими реакциями между компонентами, с учетом электромагнитных сил и др. факторов).
|
|
|
14. 2. Закон сохранения массы в термодинамике неравновесных процессов
Для многокомпонентной системы скорость увеличения массы k-ой компоненты в элементарном объёме равна потоку массы в этот объём 
, где 
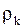- плотность, а 
- массовая скорость потока частиц данного вида. Поток в бесконечно малый элемент объёма, приходящийся на единицу объёма, есть дивергенция с обратным знаком; следовательно, уравнение баланса массы k-й компоненты имеет вид
. 
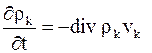(14. 1)
Для суммарной плотности 
закон сохранения имеет аналогичный вид
, (14. 2)
где v - гидродинамическая скорость среды (средняя скорость переноса массы), зависящая от координат и времени.
Для концентрации какого-либо компонента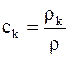 
закон сохранения массы в виде
,
где 
полная производная во времени, позволяет определить диффузионный поток
. (14. 3)
14. 3. Закон сохранения импульса в термодинамике неравновесных процессов
Изменение импульса элементарного объёма может происходить как за счёт сил, вызванных градиентом внутренних напряжений в среде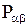 
, так и внешних сил 
.
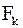Закон сохранения импульса, применённый к гидродинамической скорости, позволяет получить уравнения гидродинамики (уравнения Навье-Стокса)
, (14. 4)
где va - декартовы компоненты скорости v, а Pab-тензор напряжений.
14. 4. Закон сохранения энергии в термодинамике неравновесных процессов
Закон сохранения энергии для элементарных объёмов представляет собой первое начало термодинамики в термодинамике необратимых процессов. Здесь приходится учитывать, что полная удельная энергия складывается из удельной кинетической, удельной потенциальной энергии в поле сил 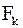и удельной внутренней энергии 
, которая представляет собой энергию теплового движения частиц и среднюю энергию взаимодействия частиц. Для удельной внутренней энергии 
получается уравнение баланса, из которого следует, что скорость изменения плотности импульса на одну частицу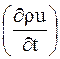 
определяется дивергенцией потоков внутренней энергии 
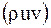и потока теплоты ( 
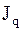), а также работой внутренних напряжений 
и внешних сил 
.
|
|
|
|
|
|
