14.5. Уравнение баланса энтропии

В термодинамике неравновесных процессов принимается, что энтропия элементарного объёма 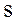(локальная энтропия) является такой же функцией от внутренней энергии 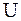, удельного объёма  и концентрации , как и в состоянии полного равновесия, и, следовательно, для неё справедливы обычные термодинамические равенства. Эти положения вместе с законами сохранения массы, импульса и энергии позволяют найти уравнение баланса энтропии

,                              (14. 5)

где s - скорость возрастания энтропии (локальное изменение энтропии на единицу объёма в единицу времени);

 - плотность потока энтропии, которая выражается через плотности потока теплоты, диффузионного потока и ту часть тензора напряжений, которая связана с неравновесными процессами (т. е. через тензор вязких напряжений ).

Энтропия (в отличие от массы, энергии и импульса) не сохраняется, а возрастает со временем в элементе объёма вследствие необратимых процессов. Положительность скорости изменения энтропии ( ) выражает в термодинамике необратимых процессов закон возрастания энтропии.

Определяется скорость изменения энтропии s только необратимыми процессами (например, диффузией, теплопроводностью, вязкостью) и равна

,                                  (14. 6)

где  - потоки (диффузионный поток - 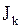, тепловой поток - 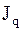, тензор вязких напряжений - );

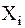 - сопряжённые им термодинамические силы, т. е. градиенты термодинамических параметров, вызывающие отклонение от равновесного состояния.

В термодинамике равновесных процессов понятие энтропии вводится как термодинамический потенциал. Если переход из одного равновесного состояния системы в другое необратим, то на участках внутри перехода рассматривать изменение энтропии как полный дифференциал уже нельзя. Можно, однако, по-прежнему найти полное изменение энтропии как разность ее значений в начале перехода системы из одного состояния в другое и в конце этого перехода.

Рассмотрим следующий простой пример. Имеется замкнутый сосуд, разделенный пополам перегородкой, не пропускающей газ, но хорошо проводящей тепло (это может быть тонкая медная фольга). Пусть в каждой половине сосуда находятся одинаковые количества одного и того же газа (идеального), но в начальный момент при разных температурах Т₁ и Т₂, причем Т₁> Т₂. Так как обе порции газа находятся в тепловом контакте, то через некоторое время температура газа в обеих половинах сосуда выравнивается и станет равной Т₃, причем T₁> Т₃> Т₂, т. е. горячий газ охладится, а холодный нагреется. Этот результат хорошо известен. Посмотрим, как в этом случае изменится энтропия всей системы. Пусть число молекул в каждом из смежных объемов одно и то же (N), а число степеней свободы каждой молекулы равно 3 (простейший случай). Тогда, так как на каждую молекулу в среднем приходится энергия  (k-постоянная Больцмана), общий запас энергии в начальный момент Е= а после установления теплового равновесия соответственно Е=3NkT₃.

Так как система замкнута, то по закону сохранения энергии

,

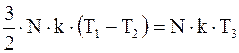откуда

T₃=(T₁+T₂)/2.

Воспользовавшись формулой для изменения энтропии при изменении объема и температуры газа. Так как в данном случае объемы не меняются в процессе эксперимента, а меняется только температура, то изменение энтропии в сумме для двух частей газа в разных половинах сосуда равно

. (14. 7)

В результате получаем, что в целом

.

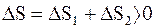Таким образом, изменение энтропии в рассматриваемом необратимом процессе положительно.

Рассмотрим второй необратимый процесс. Пусть в сосуде объемом V₁ находится одна молекула (рис. 14. 1).

Уберем перегородку (пунктир), увеличив объем сосуда до V₂. Предположим, что мы могли бы сфотографировать молекулу, перемещающуюся в сосуде 1000 раз. Тогда число фотографий, на которых частица будет зафиксирована внутри сосуда (объем V₂) будет 1000, т. е. вероятность нахождения ее в сосуде равна 1, в то время как число фотографий, на которых частица зафиксирована в объеме V₁ меньше в  раз. Если в сосуде имеется две одинаковые частицы, то вероятность одновременного нахождения ее в меньшем объеме равна произведению вероятностей нахождения каждой из них в объеме V₁, т. е. . Следовательно, вероятность нахождения частицы в меньшем объеме в 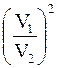 раз меньше 1 (вероятности независимых событий перемножаются).

Если же в сосуде находится N частиц, то вероятность их одновременного нахождения в меньшем объеме в  раз меньше вероятности нахождения в большем объеме V₂. Итак, число фотографий, на которых все частицы будут равномерно распределены по объему V_2, окажется в раз больше числа фотографий, на которых все частицы находились бы в меньшем объеме V₁. Вероятность микросостояния определяется соотношением

.                                           (14. 8)

Прологарифмируем это выражение (14. 8)

.                               (14. 9)

Умножим обе части (14. 9) на постоянную Больцмана k

,

где N_A - число Авогадро.

В результате получим

.                 (14. 10)

Сравнивая (14. 10) и (14. 9) приходим к выводу, что

.                                    (14. 11)

Выражение (14. 11) носит название формулы Больцмана. Энтропия возрастает с увеличением вероятности макросостояния. В этом заключается статистический смысл энтропии.

Поскольку энтропия замкнутой системы при протекании неравновесных процессов возрастает, то все неравновесные процессы идут в направлении возрастания вероятности макросостояния (т. е. совершается переход к более вероятному макросостоянию).

Вот почему при увеличении объема сосуда происходит расширение газа; тепло переходит от более нагретого тела к менее нагретому. Строго говоря, термодинамика не запрещает полностью и обратный ход процесса. Однако, вероятность его меньше, т. е. практически равна нулю.

В рассмотренных ситуациях процессы необратимые и 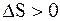. Данные результаты верны для всех необратимых процессов в замкнутых системах и обобщаются в виде весьма важного утверждения: «Во всех необратимых процессах в замкнутых системах энтропия всегда возрастает! »

При этом возрастание энтропии сопровождается и выравниванием (в нашем случае) температур или плотностей газа двух соединяемых объемов. Если под порядком понимать сосредоточение частиц или энергии в определенном месте пространства, а под беспорядком – равномерное распределение их во всем объеме, то возрастание энтропии при совершающихся без внешних воздействий необратимых процессах отражает глубокое природное стремление систем самопроизвольно, если это возможно, переходить от состояния более упорядоченного к состоянию менее упорядоченному.

Закон возрастания энтропии или закон о направлении развития любых спонтанных (самопроизвольных) процессов имеет исключительно значение. Он указывает на существование в природе преимущественного развития сложных статистических систем.

 

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: