Критическая температура и температура кипения некоторых жидкостей

 

Таблица 15. 1

Жидкость	pk атм	Tk K	Tкип при ~105 Па	Жидкость	pk атм	Tk K	Tкип при ~105 Па
Вода				Кислород
Эфир				Азот
Бензол				Водород
Углекислота				Гелий	2, 3	5, 1	4, 2

 

Если для каждой изотермы провести горизонтали p = const, разделяющие перегибы изотерм на две равновеликие по площади петли, то тем самым выделится колоколообразная кривая, в вершине которой находится критическая точка (рис. 15. 4).

По мере дальнейшего уменьшения температуры изотермы Ван-дер-Ваальса приобретают сложную форму и могут заходить даже в область отрицательных давлений.

Нужно иметь в виду, что изотермы Ван-дер-Ваальса в действительности получить не удаётся. На практике получают так называемые экспериментальные изотермы Ван-дер-Ваальса. На рис. 15. 5 представлены экспериментальные изотермы Ван-дер-Ваальса, на которых правые нисходящие ветви близки к изотермам Бойля-Мариотта. При достаточном уменьшении объема (Е) газ при обычных условиях начинает конденсироваться, образуется двухфазная система жидкость - насыщенный пар. Давление насыщенного пара зависит только от температуры, поэтому пока весь пар не превратиться в жидкость давление остается постоянным. Процесс конденсации изображается изобарой - прямой БЕ. Точка В означает окончание процесса конденсации - весь насыщенный пар превратился в жидкость.

Дальнейшее очень незначительной уменьшение объема жидкости может быть получено лишь значительным увеличением давления.

На опыте при определенных условиях удается также наблюдать участки изотермы Ван-дер-Ваальса ДЕ и ВС. Соответствующие условия сводятся к тому, чтобы в сосуде отсутствовали зародыши конденсации и парообразования в виде пылинок, кавитационных пузырьков. Состояние газа принято называть на участке ДЕ - пересыщенный пар, на участке ВС - перегретая жидкость.

С повышением температуры горизонтальные участки кривых (линий конденсации) становятся все более короткими и, в конце концов, стягиваются в критическую точку.

Причина этого явления заключается в том, что по мере повышения температуры, конденсация начинается при меньших объемах, а испарение при больших объемах V.

В точке К исчезает переход из газообразного состояния в жидкое. Исчезают фазовые переходы - процесс конденсации и процесс парообразования. При некоторой температуре Т_k, характерной для каждого вещества, исчезает разница между жидким и газообразным состояниями. Возникает так называемое критическое состояние вещества (Т_k- критическая температура). Понятие критической температуры было введено Д. И. Менделеевым в 1860 г. Критическая температура является такой температурой, выше которой пар (газ) ни под каким давлением не может быть превращен в жидкость (сжижен). Вместе с тем при критическом состоянии возможен переход пара в жидкость, минуя двухфазное состояние. В этом случае в процессе перехода вещество (газ, пар) будет все время оставаться однородным.

Таким образом, на рис. 15. 5 заштрихованная область принадлежит смеси жидкости и насыщенного пара при различных температурах (< Т_K). Слева от нее находится область жидкого состояния; справа - область парообразного состояния. Выше критической температуры Т_k опять находится однофазная область - газ (пар). Переход из газообразного состояния в жидкое может быть осуществлен либо через заштрихованную область, либо через однофазную (вокруг Т_k). Для того, чтобы сжижать газ, необходимо охладить его ниже критической температуры Т_k.

Уравнение состояния реального газа в виде (15. 3) или (15. 4) точно не выполняется потому, что поправки " a" и " b" не являются постоянными величинами. Они несколько убывают с ростом давления и температуры, а отношение " a/b" остается приблизительно постоянным. Уравнение Ван дер Ваальса совсем не применимо к структурным веществам, таким, как кристаллы, и к бесструктурным веществам в тех случаях, когда происходит диссоциация или ассоциация молекул, т. е. изменение числа молекул.

Уравнение Ван дер Ваальса можно записать в ином виде, заменив p, V и T на p_k, V_k и T_k. Обозначим p/p_k = p, V/V_k = w и T/T_k = t. Используя формулы (15. 6), (15. 7), получим уравнение состояния реального газа в виде

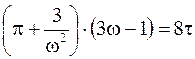.                        (15. 8)

В уравнение (15. 8) уже не входят поправки " a" и " b", поэтому при не изменяющемся роде молекул и их числе оно справедливо для всех газов. Это означает, что в относительно равных условиях состояния всех газов соответственно одинаковы.

Из уравнения Ван дер Ваальса вытекает, что

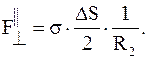.                                 (15. 9)

Из (15. 9) видно, что в правой части имеются два добавочных к RT слагаемых: одно отрицательное, зависящее от " a", и другое положительное, зависящее от " b" и " a". Влияние этих дополнительных слагаемых различно при изменении параметров газа, в частности температуры. Ту температуру, при которой эти противоположные влияния компенсируют друг друга и при которой, следовательно, реальный газ строго подчиняется закону Бойля-Мариотта, называют точкой Бойля. В соответствии с уравнением (15. 9) находится и эффект Джоуля-Томсона, имеющий существенное значение для сжижения газов. Эффект Джоуля-Томсона будет рассмотрен позднее.

15. 2. Внутренняя энергия реального газа

Внутренняя энергия реального газа состоит из двух частей: кинетической энергии поступательного и вращательного движения молекул Е_k и потенциальной энергии их взаимодействия Е_p.

В некотором приближении к реальным газам можно применить теорему о равном распределении энергии по степеням свободы, 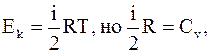 следовательно

.                                         (15. 10)

Изменение потенциальной энергии реального газа равно работе, которую совершает внутреннее давление p^' при расширении газа от объёма V₁ до V₂

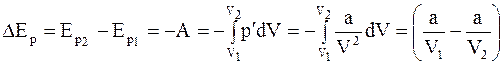. (15. 11)

Из выражения (15. 11)

.                          (15. 12)

В общем виде

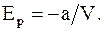                                (15. 13)

Эта энергия имеет отрицательный знак, т. к. молекулярные силы, создающие внутреннее давление внутримолекулярное давление p^', являются силами притяжения.

Таким образом, внутренняя энергия одного моля реального газа

                                (15. 14)

Из формулы (15. 14) можно получить ряд важнейших результатов. Так, например, при адиабатическом расширении газов, когда не происходит обмена теплом с окружающим пространством, внутренняя энергия реального газа не изменяется (расширение в вакуум) , а, так как

то

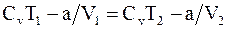.                 (15. 15)

Для разности температур будем иметь

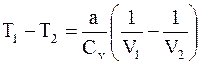.                      (15. 16)

Из (15. 16) можно сделать следующие выводы:

а) при V₂> V₁, T₁> T₂, т. е. реальный газ при адиабатическом расширении в вакуум охлаждается. Это охлаждение объясняется тем, что часть кинетической энергии теплового движения молекул переходит в потенциальную энергию их взаимодействия;

б) при V₂< V₁, T₁< T₂ – реальный газ при адиабатическом сжатии нагревается.

15. 3. Эффект Джоуля - Томсона. Сжижение газов

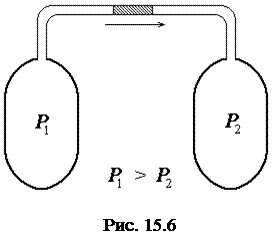Адиабатическое расширение газов с совершением положительной работы внешними силами впервые было осуществлено Д. Джоулем и В. Томсоном. Эксперимент заключался в следующем. Газ, при помощи внешней силы, действовавшей на поршень 1, " продавливался" через пористую перегородку. Расширяясь, он совершал, на другой стороне перегородки, внешнюю работу по перемещению поршня П. Давления на перегородку слева p₁ и справа p₂ поддерживались постоянными. В результате, в начале опыта, слева параметры состояния газа были p₁, V₁ и T₁, а справа газ отсутствовал, так как поршень 2 располагался вплотную к перегородке (рис. 15. 6).

После продавливания параметры состояния газа в правой части сосуда стали равными p₂, V₂, T₂. С учетом того, что газ совершал адиабатический процесс (без теплообмена с окружающей средой, Q = 0), сумма изменения внутренней энергии DU = U₂ – U₁ и работы внешних сил A должна быть равна нулю, т. е.

(U₂ - U₁) + A = 0,        (15. 17)

где А = A₁ + A₂.

При этом работа A₁, совершаемая поршнем 1 над газом, отрицательна. Ее численное значение можно определить по формуле

.                        (15. 18)

Работа A₂, совершаемая газом над поршнем 2, положительна и определяется соотношением

                                 (15. 19)

С учетом значений A₁ и A₂, формулу (15. 17) можно переписать в виде

,                  (15. 20)

где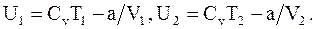

Из уравнения Ван-дер-Ваальса для моля или киломоля реального газа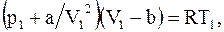

получим

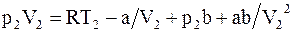; . (15. 21)

Подставив значения p₁V₁, p₂V₂, U₁ и U₂ в (15. 15), будем иметь

. (15. 22)

Рассмотрим два случая:

1. Пусть величина " a" стремится к нулю, а " b" велика, т. е. силы притяжения между молекулами газа малы, а их размеры велики, тогда

,                   (15. 23)

но p₂< p₁, следовательно

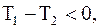 т. е. .                      (15. 24)

Таким образом, в этом случае при адиабатическом расширении газ нагревается.

2. Если величина " b" стремится к нулю, а " a" - велика, т. е. размеры молекулы малы, а силы взаимодействия между ними значительны, тогда

,

но V₂> V₁, следовательно

, т. е. .                                (15. 25)

В этом случае газ охлаждается.

Изменение температуры реального газа при расширении через пористую перегородку называется эффектом Джоуля-Томсона.

Если газ при расширении охлаждается, то эффект Джоуля-Томсона называется положительным, если нагревается - отрицательным.

В первом случае при малом значении температуры T₁ молекулы совершают работу против сил притяжения за счёт своей кинетической энергии.

Во втором случае работу совершают силы отталкивания, которые увеличивают кинетическую энергию молекул (при большем значении температуры T₂).

Следовательно, при плавном изменении температуры от T₁ до T₂ знак эффекта Джоуля-Томсона изменяется с (+) на (-). Это происходит при температуре, называемой температурой инверсии Т_i, которые для разных газов различны. Например, температура инверсии кислорода T_i ~ +790 C; водорода - T_i ~ +1800 C. Эффект Джоуля-Томсона находит широкое применение в технике при сжижении газов.

Впервые в 1823 году, используя основные выводы из рассмотренных положений, Фарадей превратил в жидкость газ хлор (CL₂). Мысль об использовании эффекта Джоуля-Томсона для сжижения газов была высказана независимо друг от друга Дьюаром (Англия) и Линде (Германия). Ими были разработаны и построены различные машины для сжижения газов.

В машине Линде получают жидкий воздух, который в газообразном состоянии сжимается компрессором до давления p~10 Н/м². После охлаждения в холодильнике он поступает в змеевик, состоящий из нескольких труб, расположенных одна в другой. Проходя по внутренней трубе, воздух подвергается дросселированию, в результате которого его температура понижается. Охлаждённый воздух по внешней трубе идёт навстречу воздуху, идущему на дросселирование, температура которого ещё больше понижается в результате теплообмена.

Такой процесс повторяется до тех пор, пока внезапное расширение не вызовет конденсацию воздуха. Жидкий воздух собирается в специальном приёмнике.

Второй промышленный метод получения сжиженных газов (метод Клода) основан на охлаждении газа при совершении им работы. Сжатый газ направляется в поршневую машину (детандер), где, расширяясь, совершает работу над поршнем за счёт запаса внутренней энергии. В результате температура газа понижается. Поршневые детандеры напоминают своим действием паровые машины, с той разницей, что в них пар заменён сжатым газом.

Этот метод был усовершенствован советским физиком П. Л. Капицей, который вместо поршневого детандера применил для охлаждения газа турбодетандер, т. е. турбину, приводимую во вращение сжатым газом. Ротор турбодетандера делает около 40000 оборотов в минуту.

Работа, совершаемая воздухом в турбодетандере, вызывает его интенсивное охлаждение, и часть воздуха сжижается. При одинаковой производительности турбодетандер в несколько раз меньше поршневого детандера.

Так, получив жидкий гелий, и заставив его кипеть при пониженном давлении, удаётся достичь температуры, всего на несколько десятых долей градуса отличающиеся от абсолютного нуля.

Для дальнейшего понижения температуры, в кипящий гелий помещают кусок железа и намагничивают его. При прекращении действия магнитного поля, происходит быстрое размагничивание железа, которое связано с затратой энергии, взятой из окружающей среды в виде теплоты.

Таким способом удалось достигнуть температур, отличающихся от абсолютного нуля на тысячные доли градуса.

Современные методы сжижения различных газов, в частности сжижение гелия, позволяют получить температуры, близкие по значению к температуре абсолютного нуля.

15. 4. Фазы и фазовые превращения. Фазовые диаграммы. Условия равновесия фаз

Испарение жидкости, плавление твердого тела являются процессами, которые называются фазовыми превращениями (переходами).

Фазовые превращения это переход вещества из одной фазы в другую, связанный с качественными изменениями свойств вещества, при изменении внешних условий. Характерной особенностью этих процессов является их скачкообразность.

Состояние вещества, между которыми происходит фазовый переход, называются фазами. В этом смысле различными фазами являются агрегатные состояния вещества: газообразное, жидкое и твердое (кристаллическое). Однако понятие фаз является более широким, чем понятие об агрегатных состояниях, так как в пределах одного и того же состояния вещества могут существовать различные фазы.

В термодинамике фаза это равновесное состояние вещества, отличающееся по физическим свойствам от других возможных равновесных состояний того же вещества.

Переход вещества из одной фазы в другую происходит (при заданном давлении) всегда при строго определенной температуре. Так при атмосферном давлении лед начинает плавиться при 0 ⁰С и при дальнейшем нагревании температура остается неизменной вплоть до момента, когда лед превратится в воду. В течение этого процесса лед и вода существуют одновременно, соприкасаясь, друг с другом. Точка перехода - значение температуры, давления или какой-либо другой величины, при котором происходит фазовый переход.

Температура, при которой происходит фазовое превращение, называется температурой фазового перехода. При температуре фазового превращения (перехода) наблюдается тепловое равновесие между двумя фазами.

В отсутствии внешних воздействий (в том числе подвода извне тепла) две фазы могут существовать неограниченно долго. При температурах выше или ниже температуры фазового перехода может существовать лишь одна (та или иная) из фаз.

При изменении давления изменяется и температура фазового перехода. Между температурой фазового перехода (превращения) вещества и давлением имеется строго определенная зависимость. Эту зависимость можно изобразить графически в виде кривой на так называемой фазовой диаграмме (диаграмме состояний), на осях координат которой откладываются давление p и температура T (рис. 15. 7). Таким образом, линии (поверхности) равновесия фаз это графики, изображающие зависимость одних термодинамических переменных от других в условиях фазового равновесия. Диаграммы состояния - совокупность линий (поверхностей) равновесия фаз. Точка на диаграмме состояния, соответствующая критическому состоянию вещества называется критической точкой. В случае двухфазного равновесия - точка окончания линии (поверхности) равновесия фаз. Состояние вещества в критической точке определяется критическими значениями температуры T_k, давления p_k и объема V_k.

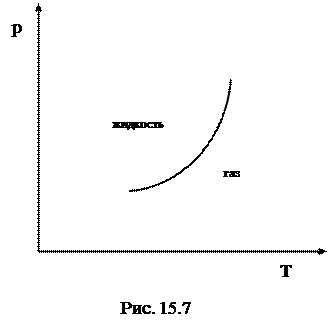Кривая фазового перехода, например, между жидкостью и ее паром, определяет условия, при которых жидкость и пар могут существовать в равновесии друг с другом. Кривая разделяет плоскость на две части, одна из которых соответствует состояниям одной фазы, а другая – состояниям другой фазы. Так как в данном случае при заданном давлении более высоким температурам соответствует пар, а более низким температурам – жидкость, то область справа от кривой соответствует газообразной фазе, а область слева - жидкой фазе. Точки самой кривой соответствуют состояниям, в которых существуют одновременно обе фазы.

Фазовую диаграмму можно изобразить не только в координатах p и T, но и в других координатах, например p, V или V, T, где V – объем, отнесенный к какому-либо определенному количеству вещества. Обычно под V подразумевается удельный объем – объем единицы массы вещества (объем, который занимает единица массы вещества).

Рассмотрим фазовую диаграмму в координатах V, T (рис. 15. 8). Пусть имеется газ с удельным объемом и температурой, соответствующими некоторой точке " а". При уменьшении объема (сжатии) газа при неизменной температуре, точка, отображающая его состояние, будет перемещаться влево по прямой, параллельной оси V. При некотором определенном давлении, которому соответствует удельный объем V_г (точка А), начнется конденсация газа в жидкость. Дальнейшее уменьшение объема (сжатие) системы количество жидкости будет возрастать, а количество газа – уменьшаться и, наконец, при достижении определенной точки (В) все вещество станет жидким с удельным объемом V_ж.

Удельные объемы газа (V_г) и жидкости (V_ж) являются функциями температуры, при которой происходит переход. Изобразив эти две функции V_г = f₁(T) и V_ж = f₂(T) получим фазовую диаграмму изображенную на рис. 15. 8. Области диаграммы справа и слева от заштрихованной части соответствуют газообразной и жидкой фазам. Заштрихованная же область между кривыми – область существования двух фаз. Горизонтальные прямые диаграммы имеют определенный смысл: точки " А" и " В" пересечения горизонтальной прямой, проведенной через некоторую точку " С" этой области, определяют удельные объемы сосуществующих в этой точке жидкости и пара. Различные точки отрезка " АВ" соответствуют равновесию одних и тех же жидкости и пара, но в различных относительных количествах. Количества пара и жидкости обратно пропорциональны длинам отрезков от точки " С" до точек " А" и " В"

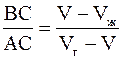.                             (15. 26)

Аналогично выглядит и диаграмма в координатах p, V. Отличие рассмотренной диаграммы (и диаграммы, построенной в координатах p, V) от диаграммы, представленной на рис. 15. 7, состоит в том, что на диаграмме в координатах p, T, область существования двух фаз сжата в одну линию. Отличие связано с тем, что находящиеся в равновесии фазы имеют одинаковые давления и температуры (согласно условиям всякого теплового равновесия); удельные же объемы этих фаз различны.

⇐ Предыдущая10111213141516171819Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: