 |
Задача № 2. Согласно Закону Дальтона, давление смеси газов равно сумме парциальных давлений компонентов: . Для определения парциальных давлений запишем уравнение Менделеева – Клапейрона для каждого компонента:
|
|
|
|
Задача № 2
Смесь водорода и азота общей массой m = 290 г при температуре T =600 К и давлении p = 2, 46 МПа занимает объем V = 30 л. Определить массу m1 водорода и массу m2 азота.
| Дано: m = 290 г = 0, 29 кг T =600 К = 6× 102 К p = 2, 46 МПа = 2, 46× 106 Па V = 30 л = 3× 10 – 2 м3 m1 = 2× 10 – 3 кг/моль m2 = 28× 10 – 3 кг/моль |
| m1 (H2) –? m2 (N2) –? |
Решение:
Согласно Закону Дальтона, давление смеси газов равно сумме парциальных давлений компонентов:
p = p1 + p2. (1)
Для определения парциальных давлений запишем уравнение Менделеева – Клапейрона для каждого компонента:
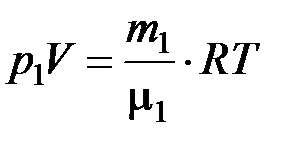, (2)
, (3)
где индексом «1» отмечены характеристики, относящиеся к водороду, а индексом «2» – к азоту. Выразим p1 и p2 из уравнений (2) и (3) и подставим в закон Дальтона (1):
; (4)
при этом m1 + m2 = m. (5)
Из (4) и (5) следует
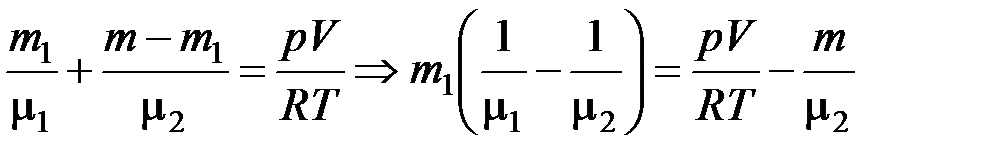. (6)
Из (6) получаем
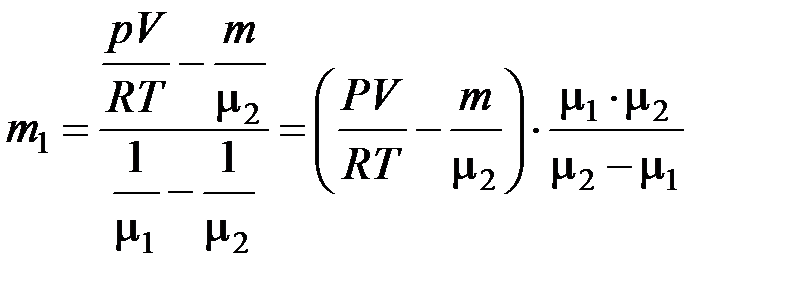. (7)
И далее находим массу азота:
m2 = m - m1.
Проверка размерности:
Расчет:
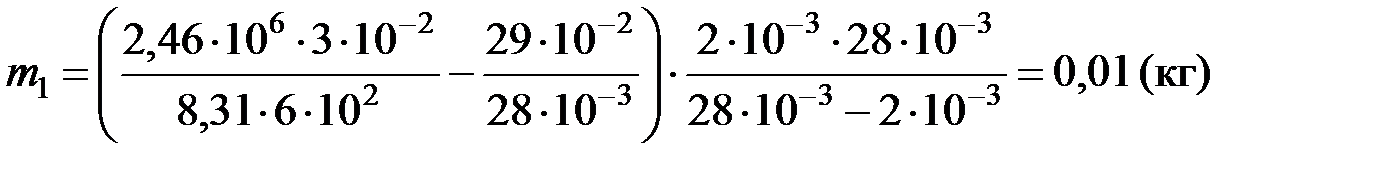
m2 = 29× 10 – 2 - 1× 10 – 2 = 0, 28 (кг)
Ответ: m1 = 0, 01 кг, m2 = 0, 28 кг.
Задача № 3
Две a-частицы, находясь первоначально достаточно далеко друг от друга, движутся по одной прямой навстречу одна другой со скоростями u и 2 u соответственно. На какое наименьшее расстояние они могут сблизиться?
| Дано: m1 = m2 = m = 6, 8× 10 – 27 кг q1 = q2 = q = 3, 2× 10 – 19 Кл u1 = u u2 = 2 u |
| rmin –? |
Решение:
Расстояние между частицами будет минимальным, когда их относительные скорости, т. е. скорости сближения, станут равны нулю. В этом случае они будут двигаться с одинаковыми скоростями.
|
|
|
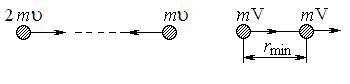
По закону сохранения импульса
2× m u - m u = 2 m V,
V = u / 2.
По закону сохранения энергии полная механическая энергия частиц сохраняется:
,
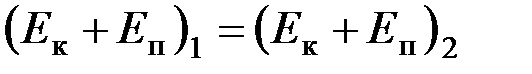где
, 
;
, 
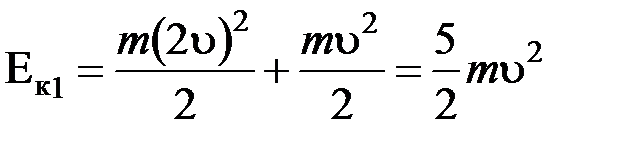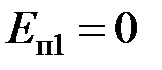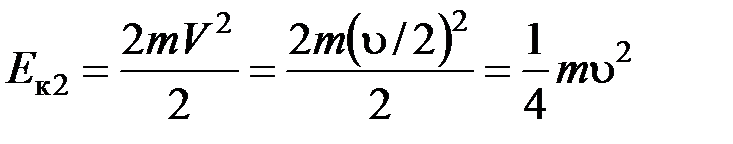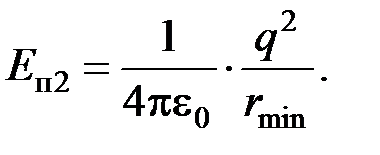
Тогда получим
, 
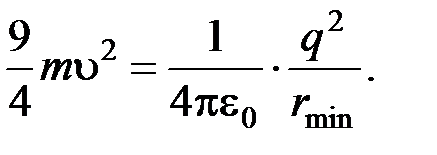
Отсюда
,
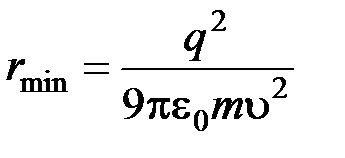где e0 = 8, 85 10 – 12 Ф/м – электрическая постоянная.
Проверка размерности:
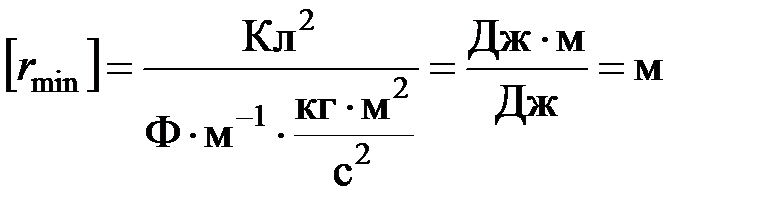
Ответ: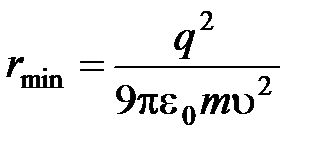 
.
Задача № 4
Тонкий провод в виде кольца массой m = 5 г свободно подвешен на неупругой нити в однородном магнитном поле. По кольцу течет ток силой i = 6 А. Период Т малых крутильных колебаний относительно вертикальной оси равен 2, 2 с. Найти индукцию В магнитного поля.
| Дано: m = 5 г = 5× 10 – 3 кг i = 6 А B = const T = 2, 2 с |
| B –? |
Решение:
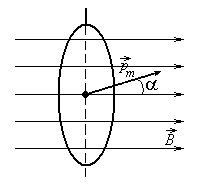
На контур с током в магнитном поле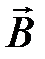 
действует момент силы N = B × pm sin a, где pm = i × S – магнитный момент кольца; S – площадь кольца.
Запишем уравнение динамики вращательного движения:
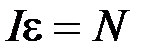, (1)
где 
– момент инерции кольца относительности оси, лежащей в плоскости кольца и проходящей через его центр; 
– угловое ускорение (вторая производная угла поворота по времени); N – возвращающий механический момент, равный N = - B × i × S × a (при малых углах sin a » a); S = p R2 – площадь кольца. Тогда уравнение (1) примет вид:
;
.
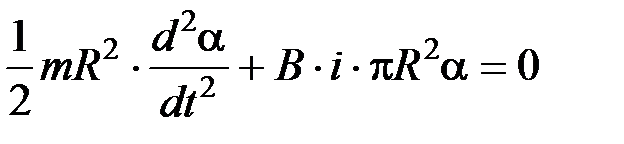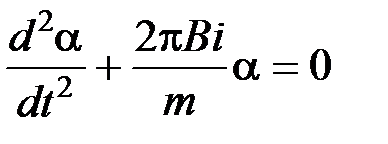Таким образом, мы получаем дифференциальное уравнение динамики гармонических колебаний, для которых циклическая частота 
.
Учитывая связь периода колебаний и частоты, имеем:
.
Отсюда
,
следовательно,
.
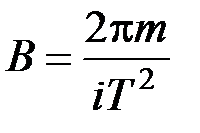Проверка размерности:
.
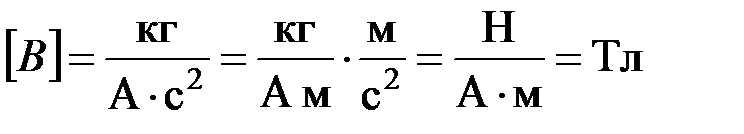Расчет:
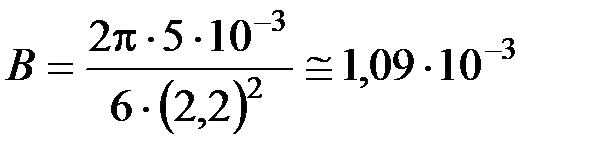(Тл).
Ответ: B = 1, 09 мТл.
Задача № 5
На дифракционную решетку нормально к ее поверхности падает монохроматический свет. Постоянная дифракционной решетки в n = 4, 6 раза больше длины световой волны. Найти общее число m дифракционных максимумов, которое теоретически возможно наблюдать в данном случае.
| Дано: d = 4, 6 l |
| m –? |
Решение:
|
|
|
По условию максимумов для дифракционной решетки
d sin j = k l, (1)
где k = 0, 1, 2, …
Модуль sin j не может превысить единицу. Поэтому из формулы (1) вытекает, что наибольший порядок наблюдаемого максимума kmax должен быть меньше отношения периода решетки d к длине волны l, т. е.:
.
Проверим размерность:
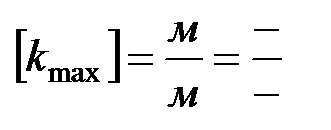
Расчет:
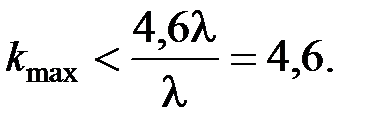
Округляем до ближайшего слева целого числа, тогда kmax = 4.
Общее количество максимумов будет равно сумме центрального максимума и числа максимумов справа и слева от центрального:
m = 4 + 4 + 1 = 9.
Ответ: 9 максимумов.
|
|
|
