 |
Равносильные переходы между уравнениями с модулями
|
|
|
|
Уравнения и неравенства с модулем на централизованном тестировании
Исполнитель:
студент группы М-51 С.М. Горский
Научный руководитель:
к.ф.- м.н., старший преподаватель В.Г. Сафонов
Гомель 2008
Оглавление
Введение
Абсолютная величина и её свойства
Простейшие уравнения и неравенства с модулем
Графическое решение уравнений и неравенств с модулем
Иные способы решения уравнений и неравенств с модулем
Метод раскрытия модулей
Использование тождества, при решении уравнений
Решение уравнений содержащих модули неотрицательных выражений
Решение уравнений с использованием геометрической интерпретации
Решение уравнений с использованием тождества
Применение теоремы о знаках при решении уравнений
Решение уравнений переходом к следствию
Решение уравнений методом интервалов
Решение уравнений домножением на положительный множитель
Типовые тестовые задачи, содержащие переменную под знаком модуля
Заключение
Список использованных источников
Введение
Понятие абсолютной величины (модуля) является одной из важнейших характеристик числа как в области действительных, так и в области комплексных чисел.
Это понятие широко применяется не только в различных разделах школьного курса математики, но и в курсах высшей математики, физики и технических наук, изучаемых в вузах. Например, в теории приближенных вычислений используются понятия абсолютной и относительной погрешностей приближенного числа. В механике и геометрии изучаются понятия вектора и его длины (модуля вектора). В математическом анализе понятие абсолютной величины числа содержится в определениях таких основных понятий, как предел, ограниченная функция и др. Задачи, связанные с абсолютными величинами, часто встречаются на математических олимпиадах, вступительных экзаменах в вузы, на ЦТ и на ЕГЭ.
|
|
|
Программой школьного курса математики не предусмотрены обобщение и систематизация знаний о модулях, их свойствах, полученных учащимися за весь период обучения. Данный пробел и пытается восполнить настоящий диплом.
Дипломная работа состоит из 5 разделов.
В первом разделе приведены равносильные определения модуля, его геометрическая интерпретация, свойства абсолютной величины. На примере показано, как используя модуль, любую систему уравнений и неравенств с одной и тоже областью определения можно представить в виде одного равносильного сравнения. Так же показано на примере, как линейный сплайн, предствавить в виде одного уравнения с модулями. Приведены примеры заданий, в которых используются либо свойства модуля, либо уравнения и неравенства, содержащие знак абсолютной величины, возникают в процессе решения.
Во втором разделе представлены методы решения простейших уравнений и неравенств с модулями, решение которых не требует использование трудоемкого процесса раскрытия модулей.
В третьем разделе представлено графическое решение уравнений и неравенств, содержащих знак абсолютной величины. Графическое решение уравнений и неравенств с модулем в некоторых случаях гораздо более простое, чем аналитическое. В этом разделе рассмотрены построение графиков функций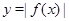 
, 
и 
. Много внимания уделено построению графиков функций, представляющих собой сумму линейных выражений под знаком абсолютной величины. Так же приведены примеры построения графиков функций с ``вложенными'' модулями. Приведены теоремы об экстремумах функций, содержащих сумму линейных выражений под знаками абсолютных величин, позволяющие эффективно решать задачи как на нахождение экстремумов подобных функции, так и решать задачи с параметрами.
|
|
|
В четвертом разделе представлены дополнительные методы решения уравнений и неравенств, содержащих знак абсолютной величины. В первую очередь описан трудоемкий и не всегда рациональный, а в некоторых случаях и неприменимый метод раскрытия модулей, иногда называемый метод интервалов, с помощью которого можно решить любое уравнение и неревенство с модулем. Описан метод использования тождества 
; рассмотрены метод геометрической интерпретации, использование тождества 
, применение теоремы о знаках, метод перехода к следствию, метод интервалов, метод домножения на положительный множитель.
В пятом разделе приведены примеры решения типовых тестовых задач связанных с понятием абсолютная величина. Приведены решения как ``стандартных'' задач, в решении которых необходимо получить какую-либо комбинацию решений, так и заданий с параметрами. Для некоторых задач приведено несколько способов решения, иногда указаны типичные ошибки возникающие в процессе решения. Для всех заданий приведено наиболее эффективное, по быстроте, решение.
Абсолютная величина и её свойства
Модуль. Свойства модуля
Определение. Модуль числа 
или абсолютная величина числа равна , если 
больше или равно нулю и равна 
, если меньше нуля:
Из определения следует, что для любого действительного числа , 
.
Теорема Абсолютная величина действительного числа 
равна большему из двух чисел или .
1. Если число положительно, то отрицательно, т. е. 
. Отсюда следует, что 
.
В этом случае 
, т. е. 
совпадает с большим из двух чисел и .
2. Если отрицательно, тогда положительно и 
, т. е. большим числом является . По определению, в этом случае, 
--- снова, равно большему из двух чисел и .
Следствие Из теоремы следует, что 
.
В самом деле, как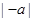 
, так и равны большему из чисел и , а значит, равны между собой.
Следствие Для любого действительного числа справедливы неравенства 
, 
.
Умножая второе равенство на 
(при этом знак неравенства изменится на противоположный), мы получим следующие неравенства: 
, 
справедливые для любого действительного числа . Объединяя последние два неравенства в одно, получаем: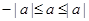 
.
|
|
|
Теорема Абсолютная величина любого действительного числа равна арифметическому квадратному корню из 
: 
.
В самом деле, если 
, то, по определению модуля числа, будем иметь 
. С другой стороны, при , 
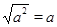, значит .
Если 
, тогда и 
и в этом случае .
Эта теорема дает возможность при решении некоторых задач заменять 
на 
.
Геометрически означает расстояние на координатной прямой от точки, изображающей число , до начала отсчета.
Если , то на координатной прямой существует две точки и 
, равноудаленной от нуля, модули которых равны.
Если 
, то на координатной прямой изображается точкой 
.
Свойства модуля
Из этого свойства следует, что 
; 
.
Равносильные переходы между уравнениями с модулями
Тема ``Абсолютная величина'' (или ``Модуль числа'') является наиболее эксплуатируемой в практике вступительных экзаменов. Вероятно, это объясняется ощущением простоты понятия абсолютной величины числа и тем обстоятельством, что, используя модуль, любую систему и совокупность уравнений и неравенств с одной и той же областью определения можно представить в виде одного равносильного сравнения.
Посмотрим, на примере, как система одного неравенства и совокупность двух неравенств преобразуется к одному равносильному уравнению.
В основе указанных преобразований лежат следующие легко доказываемые утверждения:
Вариант приведения одного отношения к равносильному ему отношению другого типа
| < | 
| 
| 
| > | ||||
| 
| 
|
| 
|
| 
| 
| 
|
| 
| 
|
| 
|
| 
| 
| 
|
|
| 
|
| 
|
| 
|
| 
|
|
| 
|
| 
|
| 
|
| 
|
|
| 
|
| 
|
| 
|
| 
|
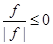
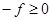
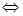
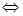
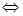
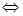
Линейные сплайны
Пусть заданы 
--- точки смены формул. Функция 
, определенная при всех 
, называется кусочно-линейной, если она линейная на каждом интервал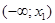е 
, 
, 
,..., 
, т. е.
где обозначено 
, 
.
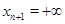Если к тому же выполнены условия согласования
то рассматриваемая кусочно-линейная функция непрерывна. Непрерывная кусочно-линейная функция называется также линейным сплайном.
|
|
|
Подобный график изображен на рисунке:
pics/ex1.eps
Функцию с графиком, показанным на этом рисунке, можно задать и одной и тремя формулами: 
Однако нетрудно заметить, что эту же функцию можно задать и одной формулой, используя модули: 
. Оказывается, что и любую непрерывную кусочно-линейную функцию вида (1) можно задать некоторой формулой вида
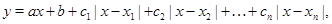
где числа 
, 
, 
,..., 
легко найти по графику данной функции.
Заметим, что две ломанные с бесконечными крайними звеньями и одинаковыми абсциссами вершин 
, 
,..., 
совпадают, если у них равны угловые коэффициенты всех ``одноименных'' звеньев и имеется общая точка. Иными словами, знание угловых коэффициентов всех звеньев и координат одной точки такой ломаной на основе указанной информации, при котором данная точка 
берется за исходную, см. рисунок.
pics/ex2.eps
Отмеченный факт мы и положим в основу получения формулы для непрерывной кусочно-линейной функции, заданной своим графиком. Напомним, что 
равняется 
, если 
, и 
, если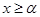 
. Поэтому на каждом из промежутков 
, 
,..., 
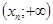, на которые числовая прямая разбивается точками, функция, определяемая формулой (), будет линейная (как сумма линейных функций), и для нахождения углового коэффициента соответствующего звена ломанной достаточно найти коэффициент при после раскрытия всех модулей в выражении () на соответствующих этим звеньям промежутках, находим:
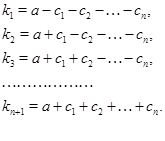
Вычитая из второго равенства первое, получаем 
вычитая из третьего второе, получаем 
и т. д. Мы приходим в итоге к соотношениям
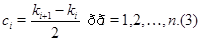
Складывая первое равенство с последним, получаем 
откуда
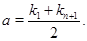
Обратно, нетрудно проверить, что из равенств (3) и () вытекают соотношения ().
Итак, если коэффициенты 
определяются формулами (3) и (), то угловые коэффициенты всех звеньев графика функции () совпадают с соответствующими угловыми коэффициентами заданного графика и, значит, остается обеспечить всего одну общую точку этих ломанных для их совпадения.
Этого всегда можно добиться выбором подходящего значения оставшегося пока не определенным коэффициента 
. С этой целью достаточно подставить в формулу (), коэффициенты которой уже вычислены из соотношений (3) и (), координаты какой-либо одной точки данной ломаной и найти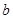 
из полученного равенства.
Пример Найдем уравнение ломаной, изображенной на рисунке (треугольный импульс).
pics/ex3.eps
Решение. Угловые коэффициенты звеньев таковы: 
, 
, 
, 
. Поэтому 
.
Значит, уравнение данной ломаной имеет вид
|
|
|
Найдем значение коэффициента из условия 
, подставляя координаты вершины (0; 1) нашей ломаной в уравнение, получим 
, откуда находим, 
, и уравнение окончательно запишем в виде
|
|
|
