 |
Простейшие уравнения и неравенства с модулем
|
|
|
|
К простейшим (не обязательно простым) уравнениям мы будем относить уравнения, решаемые одним из нижеприведенных равносильных переходов: 
Примеры решения простейших уравнений.
Пример Решим уравнение  .
.
Решение.

Ответ.  .
.
Пример Решим уравнение  .
.
Решение.

Ответ.  .
.
Пример Решим уравнение  .
.
Решение.

Ответ. 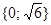 .
.
Остановимся подробнее на уравнениях, в которых встречается сумма модулей (формулы --).
Теорема Сумма модулей равна алгебраической сумме подмодульнх величин тогда и только тогда, когда каждая величина имеет тот знак, с которым она входит в алгебраическую сумму.
Пример Решить уравнение

Решение. Так как  , то мы имеем равенство вида
, то мы имеем равенство вида  , где
, где  ,
,  . Поэтому исходное уравнение равносильно системе:
. Поэтому исходное уравнение равносильно системе:


Ответ.  .
.
Теорема Сумма модулей равна модулю алгебраической суммы подмодульных величин тогда и только тогда, когда все величины имеют тот знак, с которым они входят в алгебраическую сумму, либо все величины имеют противоположный знак одновременно.
Пример Решить уравнение

Решение. ``Загоняем'' коэффициенты 2 и 5 под знак модуля и ``изолируем'' сумму модулей:

По константам получаем  . Действительно,
. Действительно,  , то есть уравнение имеет вид
, то есть уравнение имеет вид  . Следовательно, уравнение равносильно совокупности двух систем:
. Следовательно, уравнение равносильно совокупности двух систем:

то есть  .
.
Ответ.  .
.
К простейшим (не обязательно простым) неравенствам мы будем относить неравенства, решаемые одним из нижеприведенных равносильных переходов:


Примеры решения простейших неравенств.
Пример Решим неравенство  .
.
Решение.
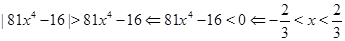 .
.
Ответ.  .
.
Пример Решим неравенство  .
.
Решение.

Ответ.  .
.
|
|
|
Как ни странно, но 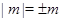 достаточно, чтобы избавиться от знака модуля в любых неравенствах.
достаточно, чтобы избавиться от знака модуля в любых неравенствах.
Пример Решить неравенство

Решение.



Ответ.  .
.
Пример Решить неравенство

Решение. Относительно любого модуля данное неравенство имеет вид  . Поэтому перебрав все комбинации знаков двух подмодульных выражений, имеем
. Поэтому перебрав все комбинации знаков двух подмодульных выражений, имеем


Ответ.  .
.
Пример При каких значениях параметра  неравенство
неравенство

выполняется при всех значениях 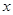 ?
?
Решение. Исходное уравнение равносильно системе:

Выполнение для всех  исходного неравенства равносильно выполнению для
исходного неравенства равносильно выполнению для  всех неравенств последней системы. А это равносильно тому, что дискриминанты всех четырёх квадратных трёхчленов неположительны:
всех неравенств последней системы. А это равносильно тому, что дискриминанты всех четырёх квадратных трёхчленов неположительны: 
Ответ.  .
.
Пример Найти все значения параметра  , при каждом из которых число целочисленных решений неравенства
, при каждом из которых число целочисленных решений неравенства

максимально.
Решение. Так как  то исходное уравнение равносильно системе:
то исходное уравнение равносильно системе:

Поскольку оба неравенства в системе линейны относительно  . Решим систему относительно
. Решим систему относительно  :
:

Условия существования параметра  равносильно требованию
равносильно требованию



Неравенство объявляет все значения  , которые могут быть решением исходного неравенства хотя бы при одном значении параметра. Следовательно, целочисленными решениями исходного неравенства могут быть только целые числа из промежутка
, которые могут быть решением исходного неравенства хотя бы при одном значении параметра. Следовательно, целочисленными решениями исходного неравенства могут быть только целые числа из промежутка  , то есть
, то есть

Естественно, что для любого целого числа из набора надо выяснить, при каких значениях параметра  это число будет решением исходного неравенства.
это число будет решением исходного неравенства.
Поскольку исходное неравенство равносильно, то поочерёдно подставляя числа из набора в неравенства, мы сразу и найдём все соответствующие значения параметра. Имеем

Чтобы выявить значения параметра, при которых исходное неравенство имеет максимальное число целочисленных решений, воспользуемся ``разверткой'', полученной информации вдоль от параметра (см. рис.):
|
|
|

Очевидно, что максимальное количество целочисленных решений равно трём, и это достигается, когда  или
или  .
.
Ответ.  .
.
Графическое решение уравнений и неравенств с модулем
Решение уравнений, содержащих знак абсолютной величины часто гораздо удобнее решать не аналитически, а графически (особенно уравнения содержащие параметры).
Построение графиков вида  ,
,  и
и 
Отметим правило построения графика функции 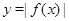 .
.
1) Строим сначала график функции 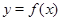 .
.
2) Там, где график функции 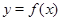 лежит выше оси
лежит выше оси  или на ней, оставляем его без изменения; точки графика, которые лежат ниже оси
или на ней, оставляем его без изменения; точки графика, которые лежат ниже оси  , заменяем симметричными им относительно оси
, заменяем симметричными им относительно оси  точками.
точками.
Для примера, на рисунке изображен график функции  .
.

Для построения графика функции  cтроим график функции
cтроим график функции  для
для  и отображаем симметрично относительно оси
и отображаем симметрично относительно оси  .
.
Для примера, на рисунке изображен график функции  .
.

Для построения графика функции  строим график функции
строим график функции 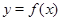 для
для  и симметрично отображаем относительно оси
и симметрично отображаем относительно оси  .
.
Для примера, на рисунке изображен график функции  .
.

Пример Построить график функции  .
.
Решение. Воспользуемся правилами преобразования графиков.
1. График функции  --- биссектриса первого и третьего координатных углов.
--- биссектриса первого и третьего координатных углов.
2. График функции  получается из графика функции
получается из графика функции  отображением его части, расположенной ниже оси абсцисс (при
отображением его части, расположенной ниже оси абсцисс (при  ) симметрично относительно оси абсцисс.
) симметрично относительно оси абсцисс.
3. График функции  получается из предыдущего сдвигом влево по оси абсцисс на две единицы.
получается из предыдущего сдвигом влево по оси абсцисс на две единицы.
4. Полученный график сдвигаем по оси ординат на 3 единицы вниз. Получаем график функции  .
.
5. Часть его, расположенную ниже оси абсцисс, отображаем симметрично относительно этой оси. Итак, получаем график данной функции (см. рис).

Исследуемая функция допускает другую форму записи 
Пример В зависимости от параметра  , найти количество решений уравнения
, найти количество решений уравнения

Решение. Построим график функции  (см. рис.).
(см. рис.).
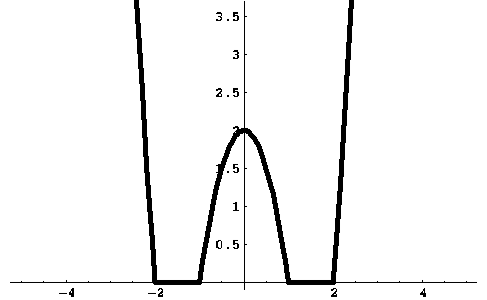
В зависимости от положения прямой  , получаем следующее: при
, получаем следующее: при  нет корней, при
нет корней, при  --- бесконечно много корней, при
--- бесконечно много корней, при  --- четыре корня, при
--- четыре корня, при  --- три корня, при
--- три корня, при  --- два корня.
--- два корня.
Пример Докажите, что на графике функции  можно отметить такую точку
можно отметить такую точку  , а на графике функции
, а на графике функции  --- такую точку
--- такую точку  , что расстояние
, что расстояние  не превышает
не превышает  .
.
|
|
|
Решение. Положим  . Точка
. Точка  с координатами
с координатами  , где
, где  , очевидно, лежит на графике функции
, очевидно, лежит на графике функции 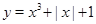 .
.
Рассмотрим положительное число  . Тогда
. Тогда  , следовательно, точка
, следовательно, точка  с координатами
с координатами  лежит на графике функции
лежит на графике функции  .
.
Расстояние между точками  и
и  равно
равно  . Но из равенства
. Но из равенства  следует, что
следует, что  ,
, 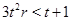 ,
, 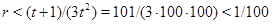 .
.
Пример На координатной плоскости изобразите все точки, координаты которых являются решениями уравнения:  .
.
Решение.  или
или  .
.
Ответ. см. рисунок

Пример Дана функция  . Сколько решений имеет уравнение
. Сколько решений имеет уравнение 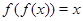 ?
?
Решение. Пусть  --- решение уравнения
--- решение уравнения 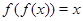 , а
, а  . Тогда и
. Тогда и  , а потому точка с координатами
, а потому точка с координатами  лежит на каждом из графиков
лежит на каждом из графиков  и
и  . Наоборот, если точка
. Наоборот, если точка  лежит на пересечении этих графиков, то
лежит на пересечении этих графиков, то 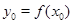 и
и 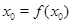 , откуда
, откуда  . Тем самым показано, что число решений уравнения
. Тем самым показано, что число решений уравнения  совпадает с числом точек пересечения графиков
совпадает с числом точек пересечения графиков  и
и  , а их 16 (см. рис.).
, а их 16 (см. рис.).
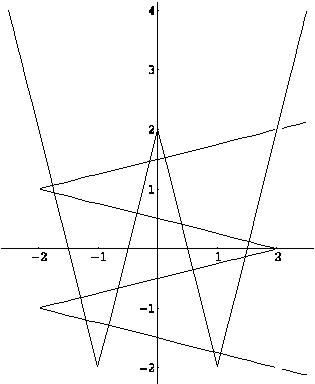 Ответ. 16.
Ответ. 16.
|
|
|


